Файл: Дискретная мат-ка_Ч.1_УП.pdf

21 

приводило к пониманию того, что многие задачи такого рода содер-
жат некоторое математическое ядро, важность которого выходит за 
рамки конкретного вопроса. Наиболее знаменитая из них – пробле-
ма четырех красок (сформулирована Де Морганом в 1850г.). 

Последние 35 – 40 лет  ознаменовали  новый  период  интенсив-

ных  разработок  в  теории  графов.  Появились  новые  области  прило-
жения:  теория  игр  и  программирование,  теория  передачи  сообще-
ния,  электрических  сетей  и  контактных  цепей,  биология,  психоло-
гия. 

2.1 

Основные

определения

2.1.1 

Общие

понятия

Граф G задается  множеством  точек  (вершин) X={x

1

,..x

n

}  и 

множеством линий (ребер) A={a

1

,..,a

  m

}, соединяющих между собой 

все или часть этих точек. Таким образом, граф G полностью задает-
ся парой (X,A). 

Другое, чаще употребляемое описание графа, состоит в задании 

множества вершин X и соответствия G, которое показывает, как ме-
жду собой связаны вершины. То есть граф задается следующим об-
разом. 

Пусть дано множество X, состоящее из элементов (назовем их 

вершинами графа) и закон G, позволяющий установить соответст-
вие  между  каждым  элементом x множества X и  некоторыми  его 
подмножествами G(x) тогда граф полностью определяется множест-
вом X и соответствием G, то есть граф 
обозначается  парой (X,G). Удобно  
использовать  обозначение G(Х)  по 
аналогии с функцией. 

Пример  (рис.2.1).  Множество 

вершин X = {x

0

, x

1

, x

2

, x

3

, x

4

, x

5

}  и 

соответствия между вершинами 

G(x

0

) = {x

1

, x

2

}, 

G(x

2

) = {x

0

, x

1

, x

5

}, 

G(x

3

) = {x

4

}, 

G(x

4

) = {x

1

, x

3

}, 

G(x

5

) = {x

2

}, 

G(x

6

) = 

∅. 

x

1

x

6

x

2

x

3

x

4

x

0

x

5

Рис. 2.1 – Пример задания 
графа 

22 

Ребра  графа – линии,  соединяющие  вершины,  указывают  на 

соответствие между вершинами в графе. 

Запись g(x

i

, x

j

) говорит, что ребро g инцидентно  вершинам x

i

, 

x

j  

 и вершины x

i

, x

j  

инцидентны ребру g. Две вершины x

i

, x

j 

назы-

ваются  смежными,  если  они  определяют  ребро  графа.  Два  ребра 
графа называются смежными, если их концы имеют общую верши-
ну.  

Вершина,  не  инцидентная  никакому  ребру  графа,  называется 

изолированной.  Если  граф  состоит  из  изолированных  вершин,  его 
называют ноль-графом. 

2.1.2 

Ориентированные

и

неориентированные

графы

Ребро  графа  называется  неориентированным,  если  порядок 

расположения  его  концов  (направление  стрелок)  в  графе  не  прини-
мается  во  внимание.  Ребро  графа  называется  ориентированным, 
если этот порядок существенен.  

В  этом  случае  говорят,  что  для 

ребра g(x

i

, x

j

) x

i 

–  начальная,  а  x

j 

–  ко-

нечная  вершины  ребра. Ориентирован-
ное ребро называют также дугой графа 
(рис.2.2). 

Граф  называется  неориентиро-

ванным,  если  каждое  ребро  его  не 
ориентированно,  и  ориентирован-
ным,  если  каждое  ребро  его  ориенти-
рованно.  Если  граф  содержит  как  ори-
ентированные,  так  и  неориентирован-

ные ребра, он называется смешанным

.

Для  каждого  графа G(Х)  существует  обратный  граф.G

-1

(Х), 

полученный  изменением  ориентации  каждого  из  ребер  графа G(Х) 
на противоположную. 

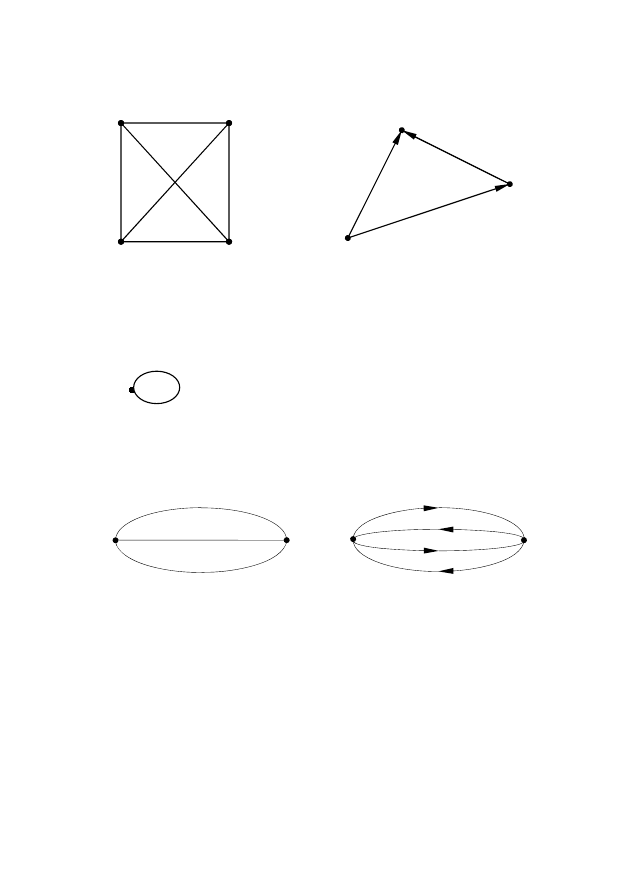
Полным неориентированным графом называется граф U(Х), 

ребрами  которого  являются  всевозможные  пары g(x

i

, x

j

,)  для  двух 

возможных x

i

, x

j 

∈X, i≠j (рис.2.3).

x

j

x

i

Рис. 2.2 – Дуга ориен-
тированного графа 

23 

 
 
 
 
 
 
 
 
Полным ориентированным графом U

0

(Х) называется граф, у 

которого любые две вершины соединены хотя бы в одном направле-
нии.  

Петлей  называется  ребро g(x

i ,

  x

i

),  у 

которого  начальная  и  конечная  вершины 
совпадают  (рис.2.4)  Петля  обычно  счита-
ется неориентированной. 

Мультиграфом  называется  граф,  в 

котором  пара  вершин соединяется несколькими различными ребра-
ми или дугами (рис.2.5). 

 
 
 
 
 
 
 
 
Дополнением графа G(Х) является такой граф G

k

(Х), ребра ко-

торого совместно с графом G(Х) образуют полный U(Х) граф. 

2.1.3 

Цепи

, 

циклы

, 

пути

и

контуры

графов

Для  неориентированных  графов  справедливы  следующие 

понятия. 

Цепь – конечная или бесконечная последовательность ребер  

g(x

i, 

x

i

) 

x

i

Рис. 2.4 - Петля 

x

3

x

2

x

1

x

4

Рис. 2.3 – Полный неориентированный и полный ориентированный        
                 графы 

x

3

x

1

x

2

x

j

x

i

x

j

x

i

Рис. 2.5 – Неориентированный и ориентированный          
                  мультиграфы 

24 

S = (…,g

1

, g

2

,…), в которой у каждого ребра g

k 

одна из вершин явля-

ется вершиной ребра g

k-1

, а другая – вершиной ребра g

k+1

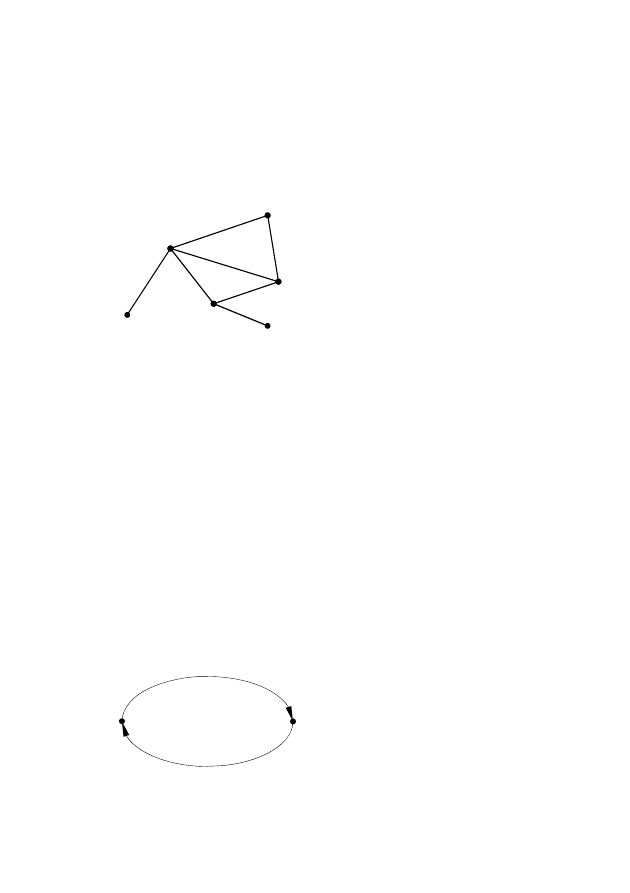
. При этом 

одно  и  то  же  ребро  или  вершина  может  встречаться  несколько  раз 
(рис.2.6):  

{g

0

, g

1

, g

2

, g

3

, g

4

, g

5

, g

2

, g

6

} = 

{(x

0

, x

1

), (x

1

, x

2

), (x

2

, x

3

),                

(x

3

, x

1

), (x

1

, x

4

), (x

4

, x

3

), (x

3

, x

2

), 

(x

2

, x

5

)}. 

Цепь  называется  про-

стой, если все ребра в ней раз-
личны,  и  составной  или 
сложной – в  противном  слу-
чае.  Вершины  в  простой  цепи 
могут повторяться. Цепь назы-
вается  элементарной,  если  в 
ней   ни   одна   из   вершин  не                  

                                                        повторяется. 
Циклом  называется  конечная  цепь,  начинающаяся  на  некото-

рой вершине x

i 

и оканчивающаяся на той же вершине. 

Простые,  составные  или  сложные,  элементарные  циклы – по 

аналогии с цепями. 

Для  ориентированных  графов  введены следующие дополни-

тельные понятия. 

Путем  в  графе G(Х)  называется    такая    последовательность  

дуг (g

1

, g

2 

,…), что конец каждой предыдущей дуги является началом 

следующей. Существуют простые, составные (сложные), элементар-
ные пути. 

Контур графа – это конечный путь, у которого начальная вер-

шина совпадает с конечной. Существуют простые, составные (слож-
ные), элементарные контуры. 

Длина пути есть число дуг L(s) в последовательности дуг пути 

s. В случае бесконечного пути L(s) = 

∞. 

 
Граф  называется  сим-

метрическим,  если   

∀ x

i

, x

j

из  того,  что  x

i 

∈ G(x

j

) 

⇒            

x

j

∈ G(x

i

), то есть две смеж-

ные  вершины  x

i

, x

j 

всегда 

g

6

g

2

g

5

g

3

g

1

g

4

g

0

x

4

x

3

x

1

x

2

x

5

x

0

Рис. 2.6 – Пример цепи 

x

j

x

i

Рис. 2.7 – Симметрический  
                  граф 

25 

соединены противоположно ориентированными дугами (рис.2.7). 

Граф называется антисимметрическим, если 

∀ x

i

, x

j

; x

i 

∈ G(x

j

) 

⇒ x

j 

∉ G(x

i

), то есть каждая пара смежных вершин соединена только 

в одном направлении.  

2.1.4 

Конечный

и

бесконечный

графы

Граф  называется  конечным,  если  число  его  вершин  конечно. 

Граф G(X) называется G – конечным, если для каждой его верши-
ны x 

∈ X множество G(x) конечно,  и  бесконечным,  если  число 

вершин бесконечно. Если обозначить |X| 

− число элементов множе-

ства X, то 

граф G(X) конечен, если |X| 

< ∞, 

граф G(X)  G – конечен, если |G(x)| 

< ∞ ∀ x ∈ X, 

граф G(X) G

-1

- конечен, если |G

-1

(x)| 

< ∞ ∀ x ∈ X. 

Граф G(X) называется локально конечным, если он одновре-

менно G - и G

-1

 - конечен. Очевидно, что всякий конечный граф ло-

кально конечен. 

2.1.5 

Частичные

графы

, 

подграфы

, 

частичные

подграфы

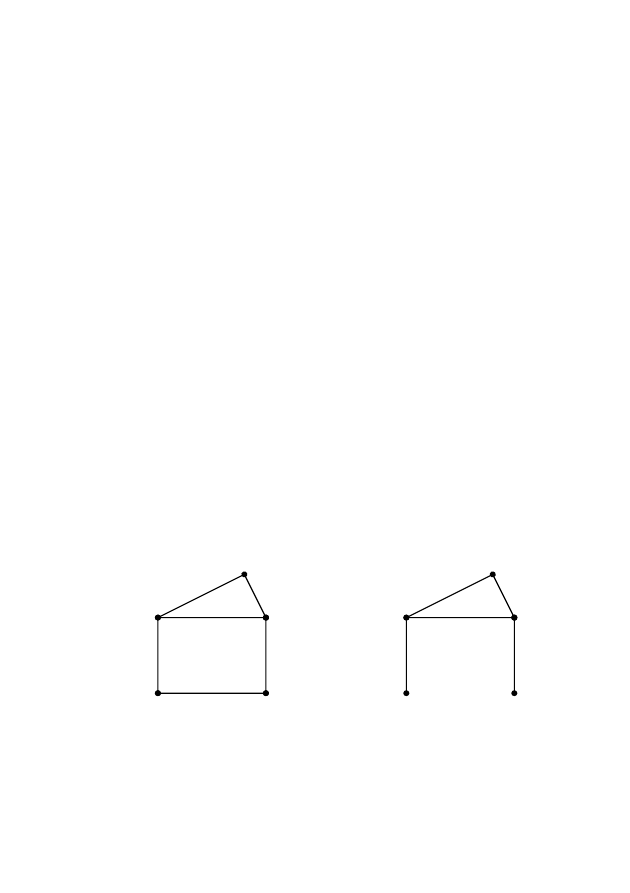
Граф H(x) называется  частичным  для  графа G(X), если  все 

ребра H(X) являются ребрами G(X) и множество вершин графа H(X) 
совпадает с множеством вершин графа G(X), то есть H(x) 

⊂ G(x) ∀  

x 

∈ X (рис.2.8). 

x

2

x

3

x

1

x

4

x

0

x

2

x

3

x

1

x

4

x

0

Рис. 2.8 – Граф G(X) и частичный для него           
                  граф H(X)