ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16643
Скачиваний: 202

16
4) теорема 2 де Моргана: дополнение пересечения есть объединение до-
полнений:
=
∩
∪
A
B
А
B.
Кроме того, применяются тождества вида
;
;
;
;
.
=
=
∅ =
= ∅
=
∪
∩
A U
U
A U
A
U
U
A
A
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Найдите элементы множества:
,
1
C
B
A
C
B
A
C
B
A
P
∩
∩
∪
∩
∩
∪
∩
∩
=
если
{
}
0,1, 2, 3, 4, 5, 6, 7, 8, 9
I
=
и известно, что
1)
{
}
0,1, 2, 5, 6 ;
A
=
{
}
1, 2, 3, 4, 9 ;
B
=
{
}
0,1, 4, 5, 7 ;
C
=
2)
{
}
0, 2, 3, 5, 7 ;
A
=
{
}
0, 6, 7, 8 ;
B
=
{
}
1, 2, 3, 7 ;
C
=
3)
{
}
1, 4, 5, 6 ;
A
=
{
}
2, 5, 6 ;
B
=
{
}
0,1, 3, 6, 9 ;
C
=
4)
{
}
0,1, 4, 5, 6 ;
A
=
{
}
2, 5, 6, 9 ;
B
=
{
}
0,1, 2, 3, 4, 6, 9 ;
C
=
5)
{
}
1, 4, 5, 8 ;
A
=
{
}
2, 4, 5, 8, 9 ;
B
=
{
}
0, 2, 3, 6, 7, 8, 9 .
C
=
2. Даны множества:
{
}
{
}
{
}
0,1, 3, 5, 6, 7 ;
1, 2, 3, 6, 8, 9 ;
1, 3, 6, 7 .
A
B
C
=
=
=
{
}
0,1, 2, 3, 4, 5, 6, 7, 8, 9 .
I
=
Найдите элементы множеств:
1)
;
1
C
B
A
C
B
A
C
B
A
P
∩
∩
∪
∩
∩
∪
∩
∩
=
2)
;
2
C
B
A
C
B
A
C
B
A
P
∩
∩
∪
∩
∩
∪
∩
∩
=
3)
.
3
C
B
A
C
B
A
C
B
A
P
∩
∩
∪
∩
∩
∪
∩
∩
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.4 Разность и симметрическая разность множеств
В теории множеств кроме основных трёх операций объединения, пересе-
чения и дополнения применяются ещё две операции, известные под названиями
разности множеств и симметрической разности.
Разность множеств
A
и
B
– это множество
C
, включающее все те эле-
менты множества
A
, которых нет в множестве
B
:
{
}
\
|
и
,
=
=
∈
∉
C
A B
x x
A
x
B

17
где наклонная черта обозначает операцию разности множеств. Иногда приме-
няется знак арифметического вычитания – минус [51].
Разность множеств
A
и
B
можно рассматривать как пересечение множе-
ства
A
с дополнением множества
B
:
\
.
= ∩
A B
A
B
Например, разность множеств (1.3) имеет вид:
{
} {
} { }
\
1, 2, 3, 4, 5 \ 3, 4, 5, 6, 7, 8
1, 2 .
C
A B
=
=
=
Симметрической разностью множеств
A
и
B
называется множество
C
,
содержащее все те элементы множества
A
, которых нет в множестве
B
, а так-
же все те элементы множества
B
, которых нет в множестве
A
:
{
}
|
и
, или
и
,
= ⊕ =
∈
∉
∈
∉
C
A
B
x x
A
x
B
x
B
x
A
где знак
⊕
обозначает операцию симметрической разности.
Через операции объединения пересечения и дополнения симметрическая
разность выражается следующим образом:
(
) (
)
\
\
.
⊕ =
=
∪
∩
∪
∩
A
B
A B
B A
A
B
A
B
Проиллюстрируем операцию симметрической разности, воспользовав-
шись примерами множеств (1.3):
{
} {
} {
}
1, 2, 3, 4, 5
3, 4, 5, 6, 7, 8
1, 2, 6, 7, 8 .
C
A
B
= ⊕ =
⊕
=
Для симметрической разности справедливы тождества:
⊕
=
A
U
A
, так как
;
⊕
=
=
∅
=
∩
∪
∩
∩
∪
A
U
A
U
A
U
A
A
A
⊕ = ∅
A
A
, так как
;
⊕ =
= ∅
∩
∪
∩
A
A
A
A
A
A
(
)
;
= ⊕ ⊕
∪
∩
A
B
A
B
A
B
,
= ⊕
∪
A
B
A
B
если
.
= ∅
∩
A
B
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Найдите элементы множества:
,
C
A
C
B
A
C
B
A
P
∩
∩
∩
∩
∩
⊕
⊕
=
если
{
}
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
I =
и известно, что
1)
{
}
0,1, 3, 4, 5, 6 ;
A
=
{
}
0, 2, 3, 4, 8 ;
B
=
{
}
0,1, 3, 5, 7 ;
C
=
2)
{
}
2, 3, 6, 7 ;
A
=
{
}
0, 4, 5, 6, 7, 8 ;
B
=
{
}
1, 2, 4, 7 ;
C
=
3)
{
}
1, 2, 3, 4, 5, 6 ;
A
=
{
}
2, 3, 5, 6 ;
B
=
{
}
0, 2, 3, 7, 9 .
C
=
2. Даны множества:
{
}
{
}
{
}
1, 2, 5, 6, 7 ;
1, 2, 4, 5, 8, 9 ;
1, 5, 6, 9 ;
A
B
C
=
=
=

18
{
}
0,1, 2, 3, 4, 5, 6, 7, 8, 9 .
I
=
Найдите элементы множеств:
1)
;
1
C
B
A
C
B
A
B
A
P
∩
∩
∩
∩
∩
⊕
⊕
=
2)
;
2
C
A
C
B
C
B
P
∩
∩
∩
⊕
⊕
=
3)
.
3
C
B
A
C
B
A
C
B
A
P
∩
∩
∩
∩
∩
∩
⊕
⊕
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.5 Диаграммы Венна
Диаграммы Венна, называемые в литературе также диаграммами Эйле-
ра – Венна [14], применяются для повышения наглядности при выполнении
операций над множествами. Множества на диаграммах Венна обычно изобра-
жаются кругами, но можно и другими замкнутыми плоскими фигурами, необя-
зательно геометрически правильной формы, а универсальные множества – пря-
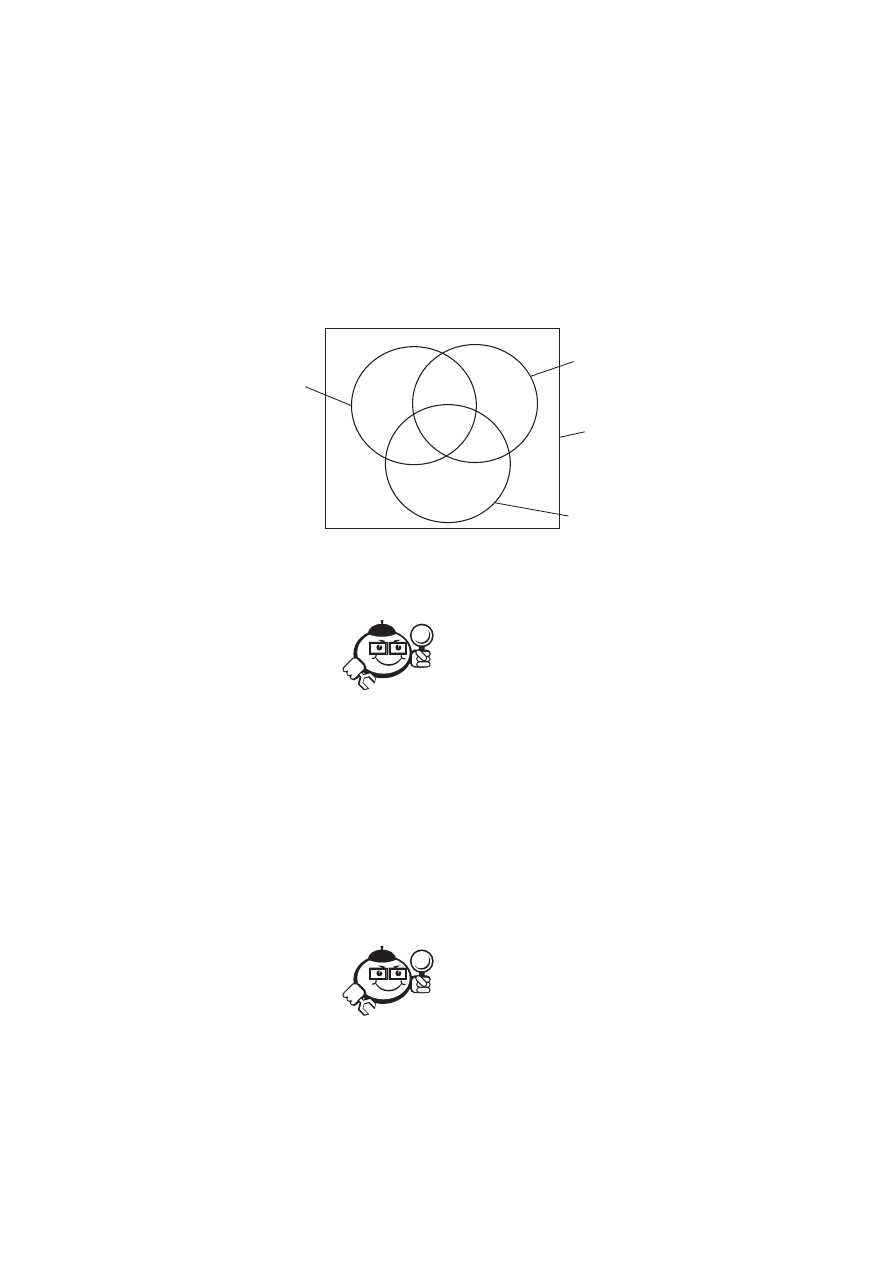
моугольниками. На рисунке 1.1 приведена диаграмма Венна для множеств вида
A = {2, 4, 6, 8}; B = {1, 2, 3, 6, 9}.
Рис. 1.1
Универсальное множества на рисунке 1.1 представлено десятичными
цифрами. Из диаграммы видно, что пересечение множеств A и B образует два
элемента. Это цифры 2 и 6:
A
∩
B = {2, 6}.
Они находятся в той части диаграммы, где круги пересекаются.
Элементы, входящие в объединение множеств, расположены в области,
ограниченной обоими кругами, следовательно:
A
∪
B = {1, 2, 3, 4, 6, 8, 9}.
Элементы 4 и 8 относятся к множеству A, но не принадлежат множес-
тву B. Следовательно, эти две цифры являются элементами разности множеств:
A \ B = {4, 8}.
1
2
3
4
6
7
8
9
5
0
A
B
U
19
Аналогично находим разность вида
B \ A = {1, 3, 9}.
Симметрическая разность определяется точно так же:
A
⊕ B = (A \ B)
∪
(B \ A) = {4, 8}
∪
{1, 3, 9} = {1, 3, 4, 8, 9}.
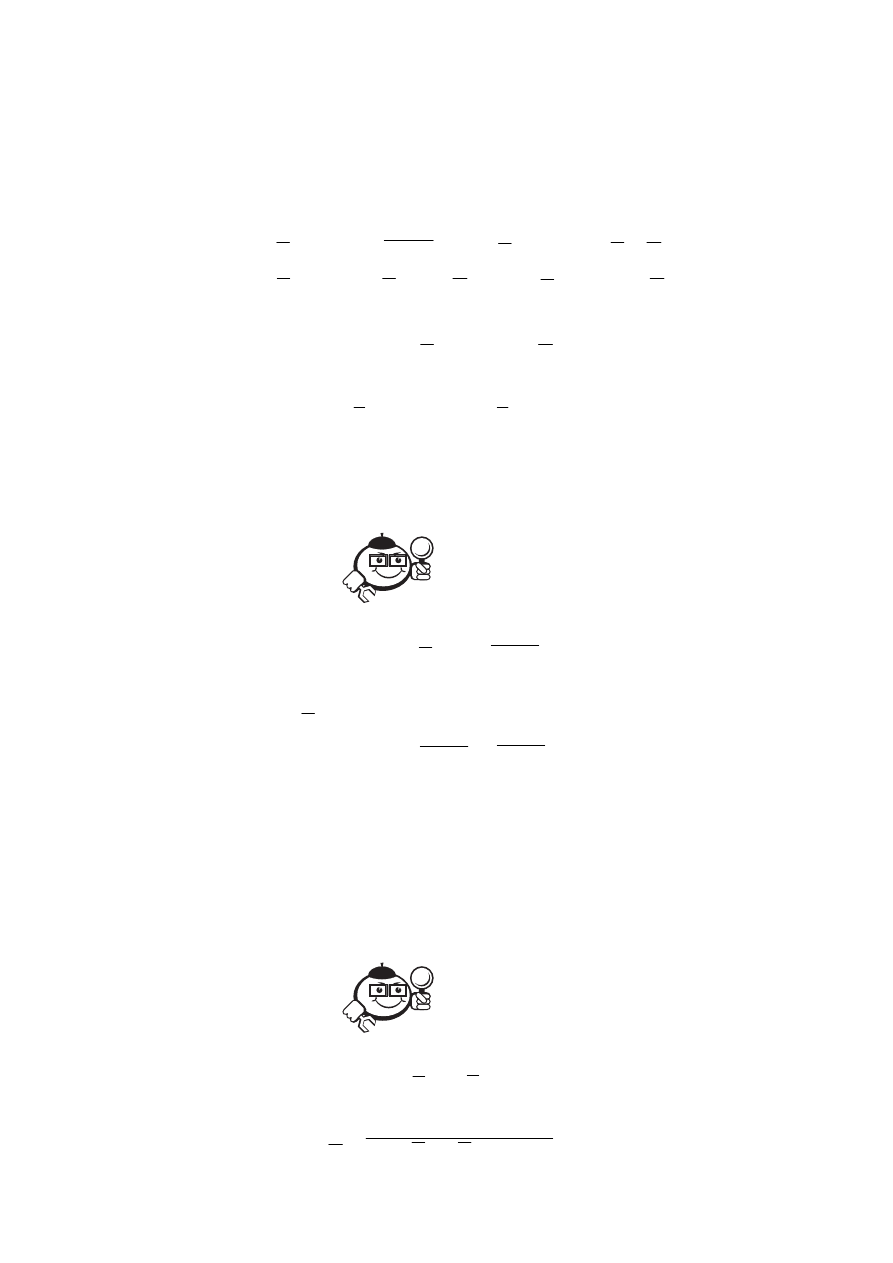
На рисунке 1.2 представлена диаграмма Венна для множеств A, B и С:
A = {0, 3, 5}; B = {0, 1, 2, 3, 7}; C = {3, 6, 7, 9},
(1.4)
для которых универсальным является множество десятичных цифр.
Рис. 1.2
Рассмотрим несколько примеров на основе множеств (1.4).
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 1.1
· · · · · · · · · · · · · · · · · · · · · · ·
Найдём элементы множества D, заданного формулой
D = A
∩
B
∪
A
∩
C.
Находим на диаграмме (рис. 1.2) области A
∩
B и A
∩
C и записываем
находящиеся в них элементы:
A
∩
B = {0, 3}; A
∩
C = {3}.
Следовательно,
D = {0, 3}
∪
{3} = {0, 3}.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 1.2
· · · · · · · · · · · · · · · · · · · · · · ·
Найти элементы множества
D = (A \ B)
∩
C
∪
[A \ (A
∩
C)].
Элементы множества D можно найти и без диаграммы, если для каждого
множества и соответствующего дополнения указать, из каких они состоят эле-
ментов. Например, сначала можно найти элементы множества (A \ B). Для этого
1
2
3
4
6
7
8
9
5
0
A
B
U
C
20
достаточно записать множество A и удалить из него элементы множества B.
Получится множество вида {5}. В множестве C элемента 5 нет, следовательно,
пересечение (A \ B)
∩
C пусто, и т. д. Однако при помощи диаграммы Венна вы-
полнить эти операции можно с гораздо меньшими трудозатратами. Сначала за-
данное выражение упростим:
D =
C
A
A
C
B
A
∩
∩
∪
∩
∩
=
)
(
C
A
A
C
B
A
∪
∩
∪
∩
∩
=
=
)
C
A
A
A
C
B
A
∩
∪
∩
∪
∩
∩
=
.
C
A
C
B
A
∩
∪
∩
∩
Затем переходим к диаграмме. Согласно последней формуле отыскиваем
на диаграмме (рис. 1.2) области
C
B
A
∩
∩
и
C
A ∩
и записываем принадлежа-
щие им элементы:
{ }
;
0,5 .
= ∅
=
∩
∩
∩
A
B
C
A
C
Таким образом, искомое множество D имеет вид:
D =
∅ ∪
{0, 5} = {0, 5}.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 1.3
· · · · · · · · · · · · · · · · · · · · · · ·
Найти элементы множества
D = A
∩ B ∩
C
∪
B
A∩
.
В предыдущем примере показано, что на диаграмме область, описывае-
мая формулой вида
A ∩ B ∩ C
, пуста. Тогда
D
=
∅ ∪
B
A ∩
=
B
A ∩
.
Множество
A ∩ B
на диаграмме (рис. 1.2) содержит элементы 0 и 3. Сле-
довательно, его дополнение образуют все элементы универсального множества,
за исключением цифр 0 и 3.
Таким образом, искомое множество имеет вид
D
= {1, 2, 4, 5, 6, 7, 8, 9}.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 1.4
· · · · · · · · · · · · · · · · · · · · · · ·
Найти элементы дополнения множества
D
= (
A ∪ B
)
∩
(
А ∪
B ∪ C
).
Сначала находим дополнение по теореме де Моргана:
D
=
∪
∩
∪
∪
)
(
)
(
C
B
A
B
A
=