ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7082
Скачиваний: 35

66
Глава 4. Переключательные функции
Количество вершин в каждом ярусе можно подсчитать по формуле (4.1)
1
:
∑
i
⎛
⎝
n
j
! ⋅
( ∏
∑ l
i
=2
n
(l
i
)!)
−1
⎞
⎠
j
.
(4.1)
Так, количество вершин во втором ярусе равно: n
j
— количество разрядов, в ко-
торых могут встречаться символы 1,1; n
j
= 3, n
(l
i
) = 2 (так как «1» встречается
сразу в двух разрядах). Символ «2» может встречаться только в одном разряде —
n
j
= 1, n
(l
i
) = 1 (n(l
i
) — количество символов). Отсюда имеем:
3! ⋅
(2!)
−1
+
1! ⋅
(1!)
−1
= 3 + 1 = 4.
Рассчитаем количество вершин в первом ярусе. Первому ярусу соответствуют
вершины, которые взвешены значениями функции f
(x
1
, x
2
, x
3
) = {3,1,2}.
Выпишем из таблицы 4.1 вектора, соответствующие этим значениям:
f
(x
1
, x
2
, x
3
) = 3 {(000), (001), (101), (211)}
f
(x
1
, x
2
, x
3
) = 1 {(010), (111), (200), (201)}
f
(x
1
, x
2
, x
3
) = 2 {(100)}
Применяя формулу (4.1), учитываем, что вектора вершин смежных должны от-
личаться только в одном разряде и всего на «1» и сумма фаз переменных векторов
равна i (i — номер фазы; фаза — это значение переменной).
Определяем данные для формулы (4.1):
∑
i
⎛
⎝
n
j
!
(∏n(l
i
)!)
−1
⎞
⎠
,
i
= 1, n
j
= 3 (так как кортеж имеет длину l = 3 — количество разрядов, в которых
встречается «1»); каждый разряд содержит только «1», которая может повторяться
n
(l
i
) раз; n(l
i
) = 2 («1» только в одном разряде).
Будем размещать символы 0,0 в n
j
= 3 разрядах. Тогда n
(l
i
) = 2. Теперь количе-
ство вершин определяется по формуле:
∑
i
(n
j
!
(∏n(l
i
)!)
−1
) =
⎛
⎝
n
j
!
(∏n(l
i
)!)
−1
⎞
⎠
= 3! ⋅
(2!)
−1
= 3,
так как i
= 1, то число вершин первого яруса равно 3 (i = 1, так как рассматриваем
только одну комбинацию символов: «0,0»).
Количество вершин третьего яруса:
• символ «2» — в одном разряде, n
j
= 1, n
(l
i
) = 1;
• символ «0,1» — в двух разрядах, n
j
= 2, n
(l
i
) = 2;
• символ «1,1,1» — один раз;
•
∑
i
=3
(n
2
!
(n(l
i
)!)
−1
) = 1! ⋅ (1!)
−1
+
2! ⋅
(2!)
−1
+
1
= 3.
1
Количество размещений из n по l элементов с повторениями.
4.2 Булевы функции (БФ)
67
Задание переключательной функции графом Кёнига.
Для задания ПФ графом Кёнига используется таблица Вейча (табл. 4.2).
Каждая вершина яруса взаимно однозначно сопоставляется вектору, определя-
емому соответствующими переменными.
Ребро, соединяющее вершину одного яруса с вершиной другого, соответству-
ет вектору X
=
(x
1
, x
2
, . . ., x
n
), который определяет значение функции f (x
1
, x
2
, . . ., x
n
).
Для геометрического отображения значения функции f
(x
1
, x
2
, . . ., x
n
) каждому реб-
ру поставим в соответствие число-значение, которое принимает f
(x
1
, x
2
, . . ., x
n
) на
соответствующем наборе значений переменных.
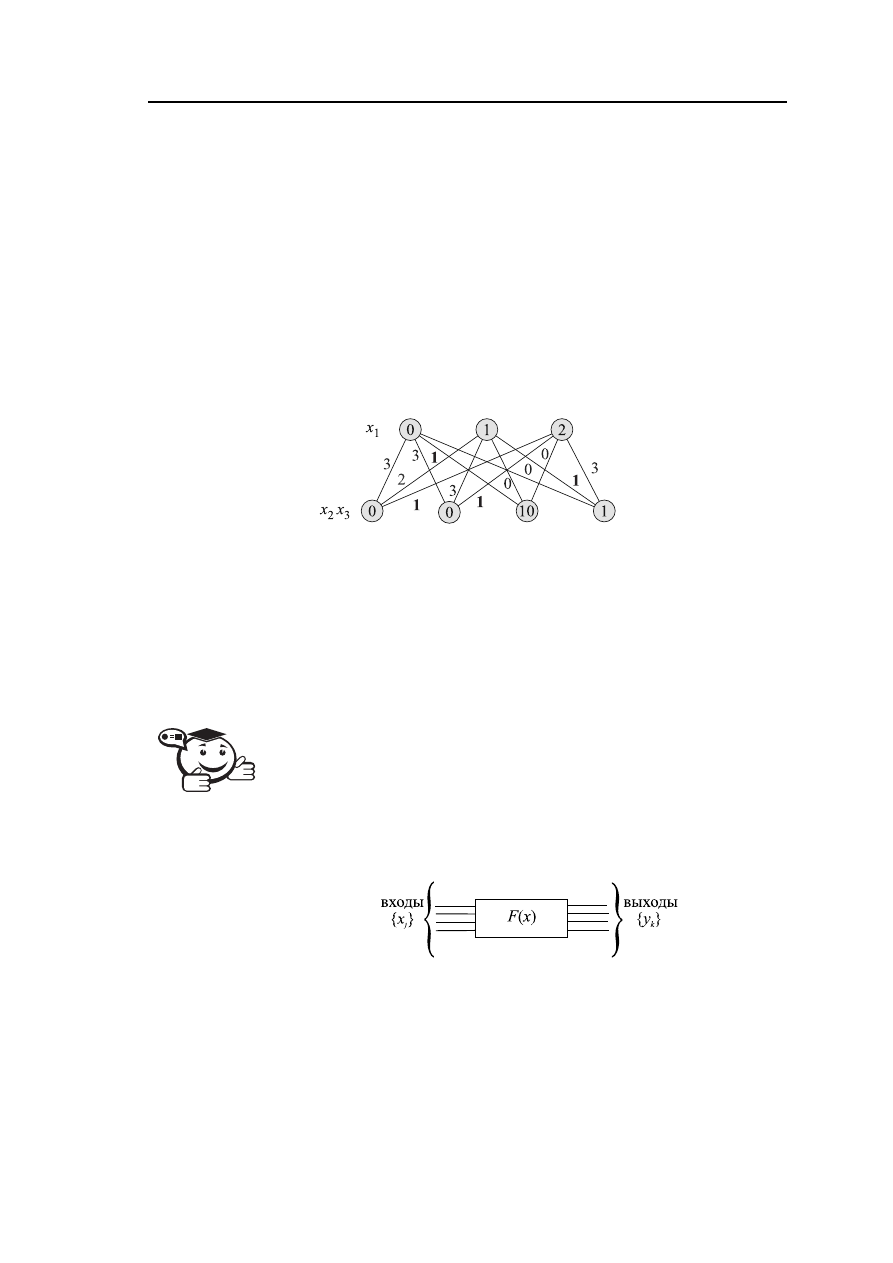
Для рассматриваемой функции f
(x
1
, x
2
, x
3
) граф Кёнига представлен на рисун-
ке 4.4.
Рис. 4.4 – Граф Кёнига
4.2 Булевы функции (БФ)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Булева функция — это функция, аргументы которой и сама
функция принимают значения на множестве B
=
{0,1}, элемен-
тами которого являются формальные символы 1 и 0, интерпрети-
руемые как «да» и «нет».
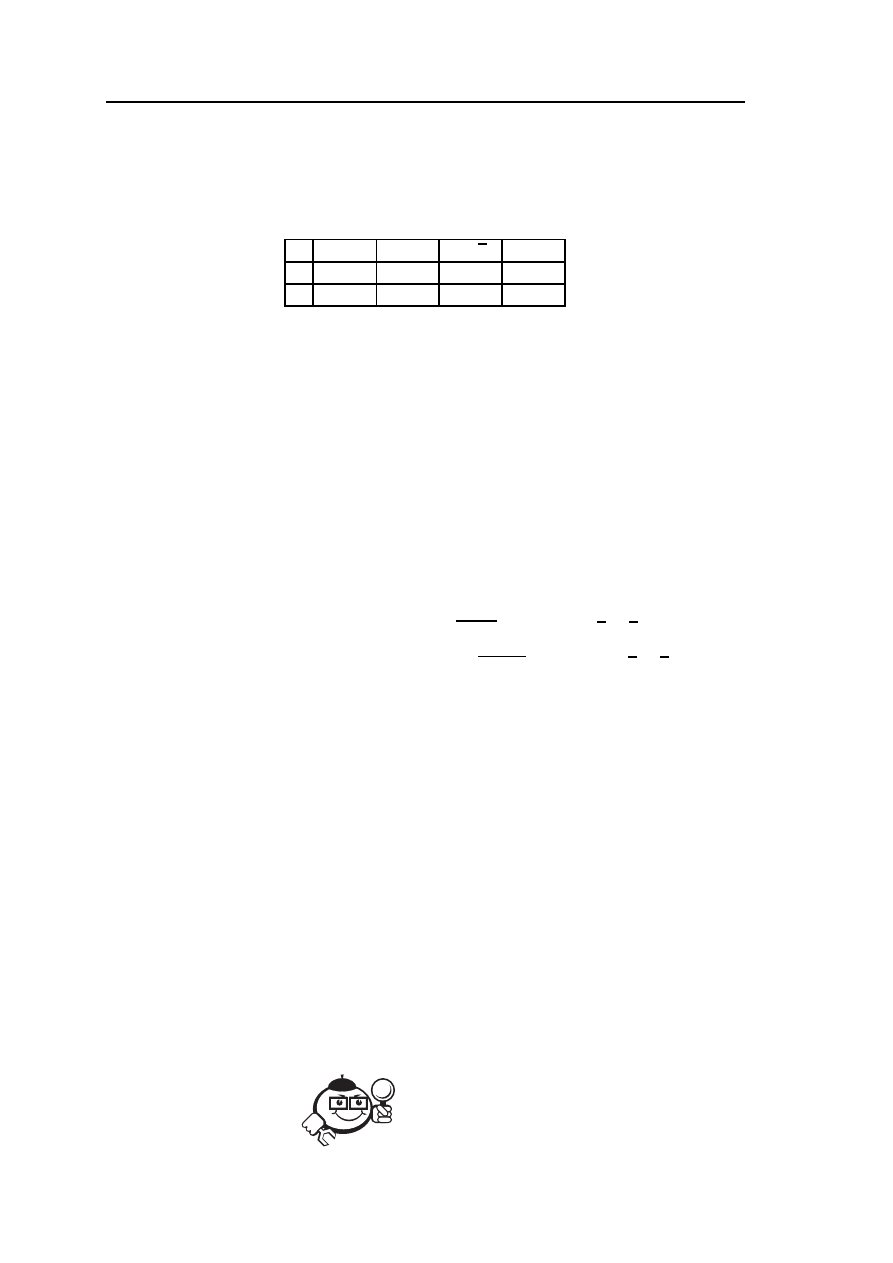
2. Булева функция — это математическая модель дискретных
устройств переработки информации:
• На вход устройства подаётся одна комбинация, которой
закодирована некоторая информация, на выходе получают
другую комбинацию.
• Количество наборов комбинаций переменных — 2
n
, где n —
число переменных.
• Количество различных БФ — 2
2
n
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
Глава 4. Переключательные функции
Множество всех булевых функций одной переменной представлено в табли-
це 4.3.
Таблица 4.3 – Булевы функции одного аргумента
x
БФ(0)
БФ(x)
БФ(x)
БФ(1)
0
0
0
1
1
1
0
1
0
1
f
0
f
1
f
2
f
3
Булева функция иначе называется логической функцией или переключательной
функцией. БФ можно задавать теми же способами, что и любую переключательную
функцию.
4.3 Аналитическое представление булевых функций
Логическая функция может быть задана формулой, содержащей символы пе-
ременных, знаки операций и скобки, либо суперпозицией, содержащей вместо пе-
ременных функции, определяющие их.
Логическая функция может быть задана эквивалентными формулами.
Например:
f
8
∶
x
1
↓ x
2
(функция Пирса),
f
8
= x
1
∨
x
2
или
f
8
= x
1
∧
x
2
;
f
14
∶
x
1
∣x
2
(функция Шеффера), или f
14
= x
1
∧
x
2
x
1
или f
14
= x
1
∨
x
2
.
Рассмотрим способы получения эквивалентных формул для представления бу-
левых функций.
Переключательная функция называется монотонной, если при любом возрас-
тании набора значения этой функции не убывают (наборы 0; 1 и 1; 0 несравнимы).
f
2
— немонотонна, так как на (1; 0) она равна «1», а на (1; 1) — «0»; f
3
— моно-
тонна; f
5
— монотонна.
Пусть дано множество исходных функций (конечное или бесконечное)
∑{f
1
, f
2
, . . ., f
m
}.
Символы переменных будем считать формулами глубины «0». Формула F име-
ет глубину k + 1, если F имеет вид
f
i
(F
1
, F
2
, . . ., F
n
i
),
где f
i
∈
∑, n
i
— число аргументов f
i
, а F
1
, F
2
, . . ., F
n
i
— формулы, максимальная из
глубин которых равна k. F
1
, F
2
, . . ., F
n
i
— подформулы F, f
i
— внешняя или главная
операция формулы F. Все подформулы формул F
1
, F
2
, . . ., F
n
i
также называются
подформулами F.
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.4
. . . . . . . . . . . . . . . . . . . . .

4.3 Аналитическое представление булевых функций
69
1. f
2
(x
1
, x
2
, x
3
) — формула глубины 1,
2. f
3
(f
1
(x
3
, x
1
),f
2
(x
1
, f
3
(x
1
, x
2
))) — формула глубины 3, так как она содержит од-
ну подформулу глубины 2 — f
2
(x
1
, f
3
(x
1
, x
2
)) — и две — глубины 1 — f
1
(x
3
, x
1
)
и f
3
(x
1
, x
2
).
Пусть: f
1
— дизъюнкция, f
2
— конъюнкция, f
3
— сложение по модулю 2.
Тогда f
3
(f
1
(x
3
, x
1
),f
2
(x
1
, f
3
(x
1
, x
2
))) запишется: (x
3
∨
x
1
) ⊕ (x
1
∧
(x
1
⊕
x
2
)).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Правила подстановки формулы вместо переменной.
При подстановке формулы F вместо переменной x все вхождения переменной x
в исходное соотношение должны быть заменены одновременно формулой F.
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.5
. . . . . . . . . . . . . . . . . . . . .
Сделаем подстановку в формулу x ∨ x
= 1, подставив в неё вместо переменной x
формулу F.
Соотношение F ∨ F
= 1 получено по правилу подстановки и верно для любых F.
Соотношение F ∨ x
= 1 получено с нарушением правила подстановки и для
некоторых F может быть неверным.
Правило подстановки позволяет получать из исходных соотношений новые эк-
вивалентные соотношения.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Во всякой алгебре, в том числе и в булевой алгебре, равенство F
1
= F
2
означа-
ет, что формулы F
1
и F
2
описывают один и тот же элемент алгебры, то есть одну
и ту же логическую функцию. Если какая-либо формула F содержит подформу-
лу F
1
, то замена F
1
на F
2
не изменяет элемента булевой алгебры f , над которым
производится операция в формуле F.
Формула F
′′
, полученная такой заменой, эквивалентна F. Это утверждение
представляет собой правило замены подформул. Оно позволяет получать форму-
лы, эквивалентные данной.
Рассмотрим разницу между правилами подстановки и замены.
При подстановке:
• переменная заменяется на формулу;
• формула может быть любой, но требуется её одновременная подстановка
во все вхождения переменной.
При замене:
• любая подформула может быть заменена, но не на любую другую, а только
на эквивалентную. При этом замена всех вхождений исходной подформулы
не обязательна.

70
Глава 4. Переключательные функции
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.6
. . . . . . . . . . . . . . . . . . . . .
Пусть имеется эквивалентность F
1
= F
2
, где F
1
и F
2
содержат переменную x.
Если вместо всех вхождений x в F
1
и F
2
подставить произвольную формулу F,
то получаются новые формулы F
′
1
и F
′
2
, причём не обязательно F
1
= F
′
1
; F
2
= F
′
2
,
однако между собой F
′
1
и F
′
2
будут эквивалентны.
Возьмём:
x
1
x
2
°
F
1
= x
1
∨
x
2
´¹¹¹¹¸¹¹¹¹¶
F
2
.
(4.2)
Подставим x
1
x
3
вместо x
1
.
Получим:
x
1
x
3
x
2
²
F
′
1
= x
1
x
3
∨
x
2
´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶
F
′
2
.
(4.3)
Причём F
1
не эквивалентна F
′
1
;
F
2
не эквивалентна F
′
2
;
однако F
′
1
эквивалентна F
′
2
.
Если в правой части (4.3) x
1
x
3
заменить формулой x
1
∨
x
3
, эквивалентной ей
в силу
(x
1
x
2
= x
1
∨
x
2
), а в полученной подформуле x
1
заменить на эквивалент-
ную формулу x
1
(в силу x
= x), то все формулы в построенной цепи преобразо-
ваний — x
1
x
3
x
2
⇒ x
1
x
3
∨
x
2
⇒ x
1
∨
x
3
∨
x
2
⇒ x
1
∨
x
3
∨
x
2
эквивалентны. Это и есть
эквивалентные преобразования.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Эквивалентные преобразования при доказательстве эквивалентности формул
более эффективны, нежели их вычисления на наборах значений аргументов (пере-
менных).
Основные правила эквивалентных преобразований.
В булевой алгебре принято опускать скобки в случаях:
1) при последовательном выполнении нескольких «∧» или «∨» (например,
вместо x
1
(x
2
x
3
) пишут x
1
x
2
x
3
);
2) если они являются внешними скобками у «∨»-и. Например, вместо
(x
1
(x
2
∨
∨
x
3
) ∨ (x
4
x
5
)) пишут x
1
(x
2
∨
x
3
) ∨ x
4
x
5
.
Упрощение формул (получение эквивалентных формул, содержащих мень-
шее число символов).
Рассмотрим основные законы, определяющие эти операции:
1. Закон поглощения
x ∨ xy
= x; x
(x ∨ y) = x.
Доказательство:
а) x ∨ xy
= x & 1 ∨ xy = x
(1 ∨ y) = x & 1 = x,
б) x
(x ∨ y) = xx ∨ xy = x ∨ xy = x.