ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7085
Скачиваний: 35
56
Глава 3. Экстремальные задачи на графах
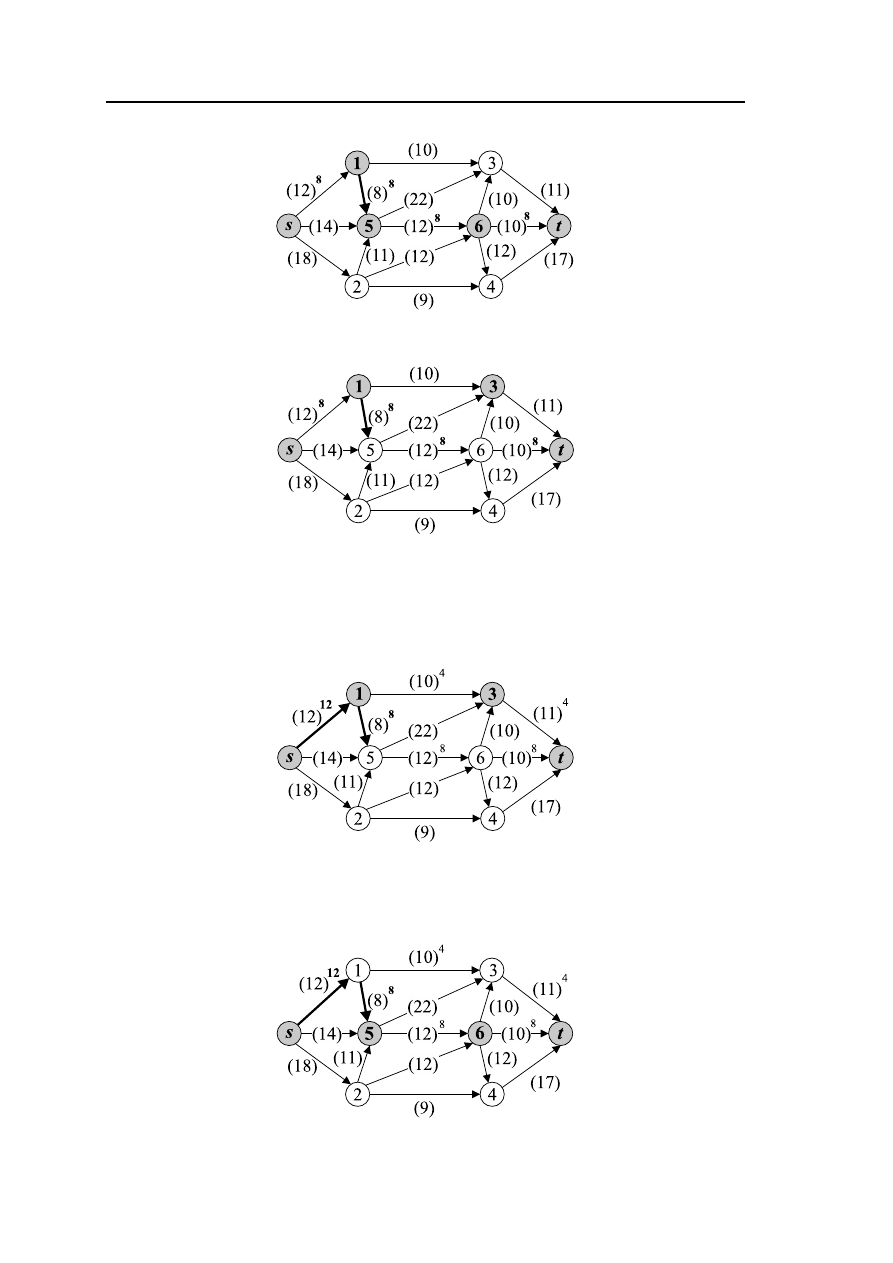
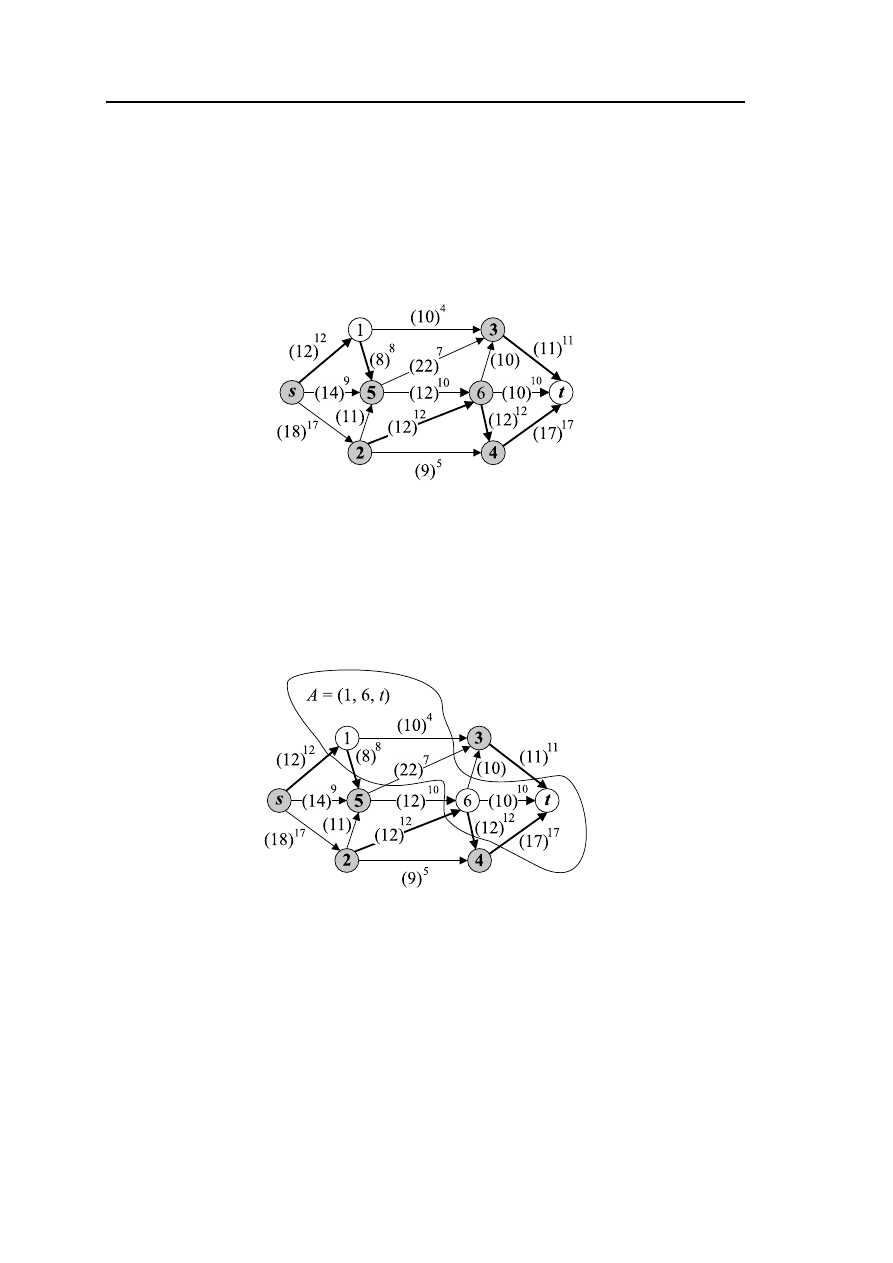
Рис. 3.5 – Сеть G
Рис. 3.6 – Сеть G
Увеличиваем величину потока на каждой дуге пути s
→ 1 → 3 → t на 4.
Отмечаем насыщенную дугу
(s,1) (рис. 3.7).
Рис. 3.7 – Сеть G
5. Выбираем следующий путь, ведущий из s в t: s
→ 5 → 6 → t (рис. 3.8).
Рис. 3.8 – Сеть G
3.3 Оптимальные потоки в транспортных/информационных сетях
57
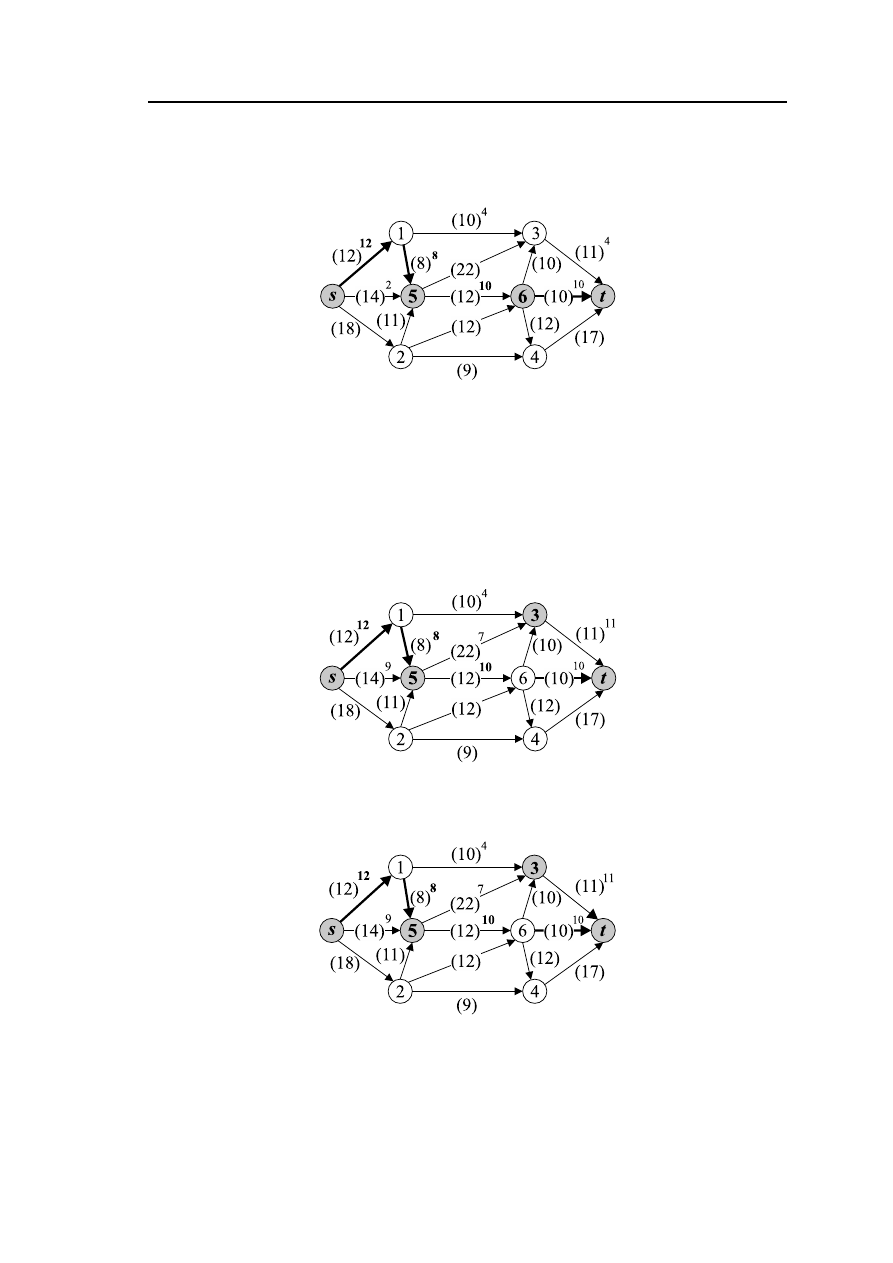
Увеличиваем величину потока на каждой дуге пути s
→ 5 → 6 → t.
Насыщенной становится дуга
(6,t) (рис. 3.9).
Рис. 3.9 – Сеть G
6. Дальнейшие аналогичные действия, связанные с увеличением потока на се-
ти, отражены на рисунках 3.10–3.18. Все оставшиеся вычисления и выкладки пред-
лагается провести самостоятельно в качестве упражнения.
Для однозначности, отметим лишь последовательность рассматриваемых путей:
s
→ 5 → 3 → t (рис. 3.10–3.12); s → 2 → 6 → 4 → t (рис. 3.13–3.14); s → 2 → 4 → t
(рис. 3.15–3.18).
Рис. 3.10 – Сеть G
Рис. 3.11 – Сеть G
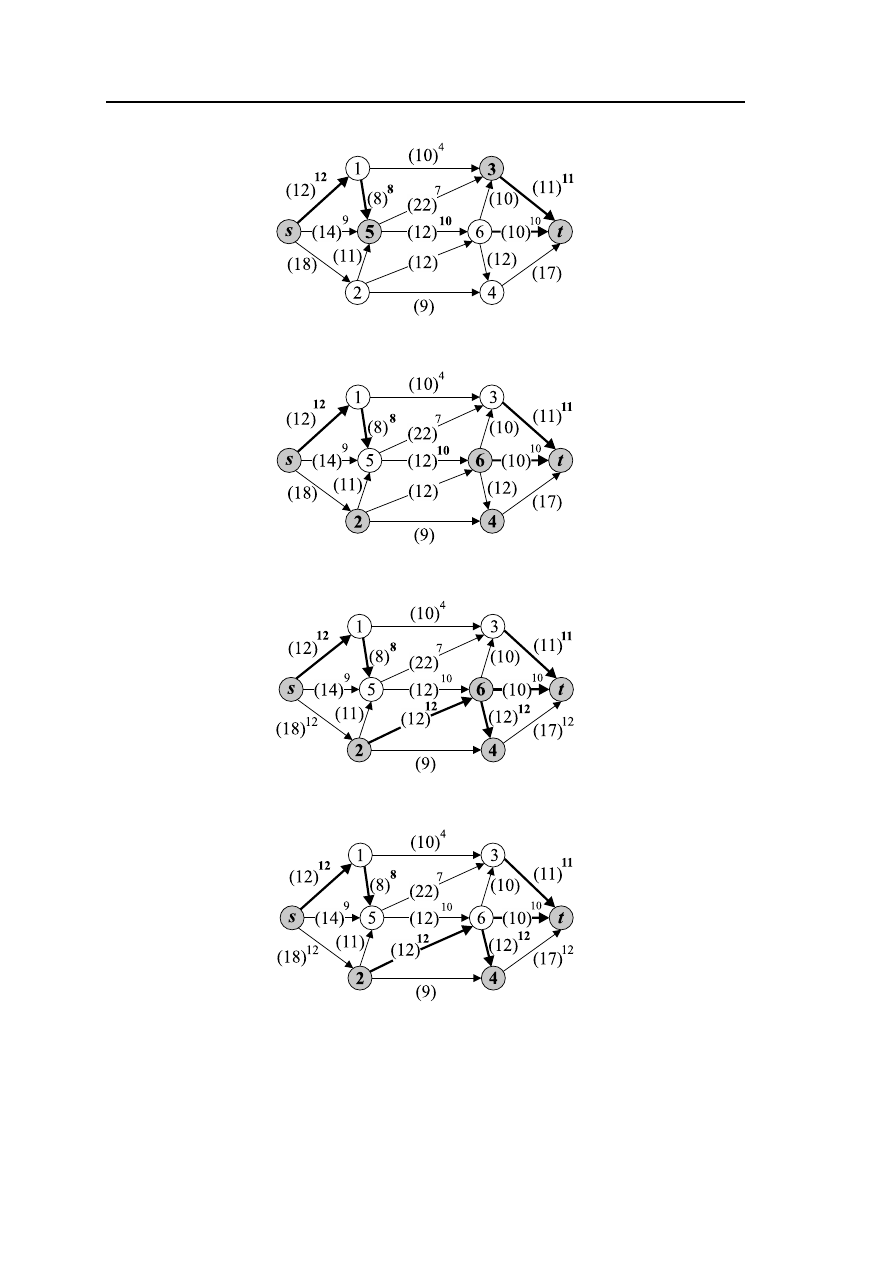
Путь s
→ 2 → 6 → 4 → t (рис. 3.13–3.14).
Путь s
→ 2 → 4 → t (рис. 3.15–3.18).
58
Глава 3. Экстремальные задачи на графах
Рис. 3.12 – Сеть G
Рис. 3.13 – Сеть G
Рис. 3.14 – Сеть G
Рис. 3.15 – Сеть G
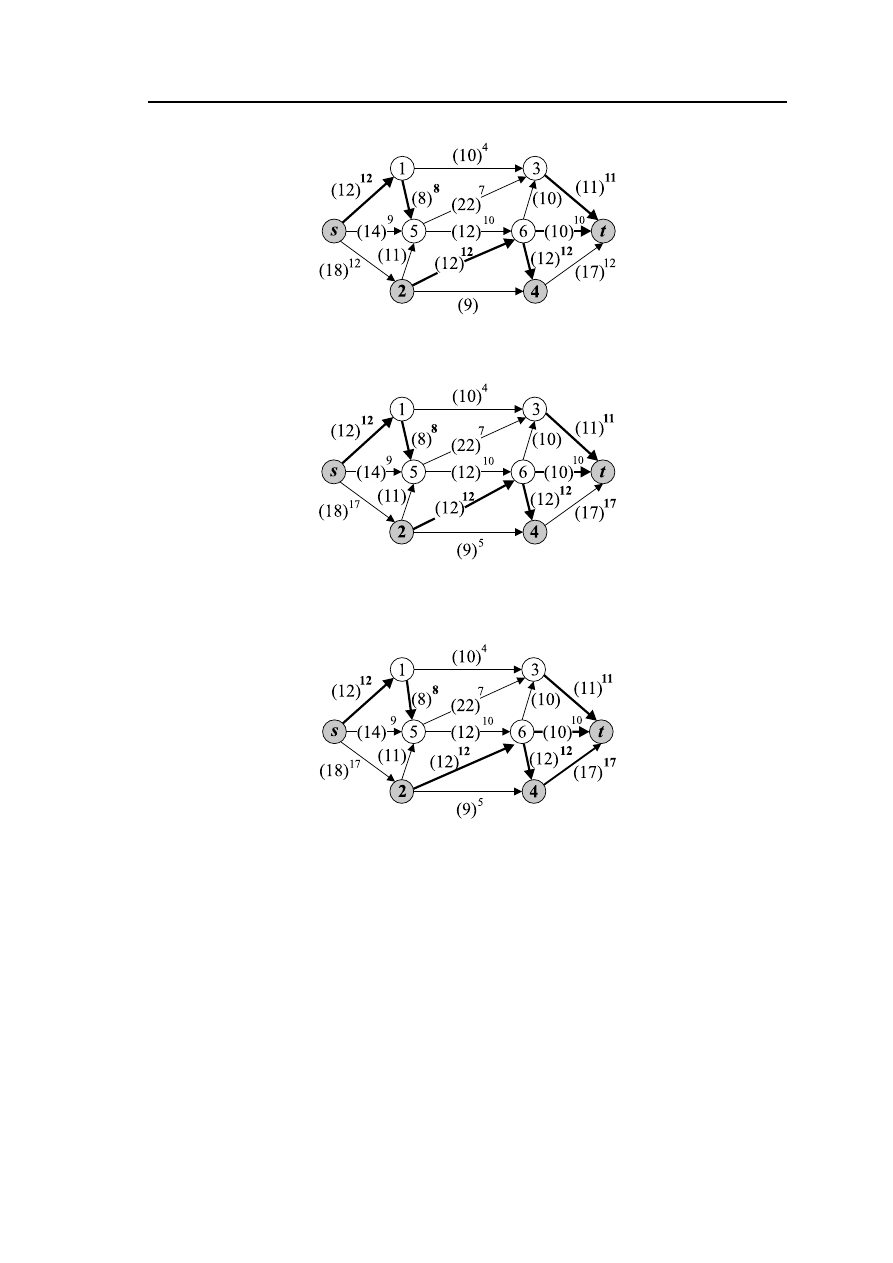
7. Выполнив действия, связанные с увеличением допустимого потока в сети от
вершины s к вершине t, переходим к построению минимального разреза сети T.
3.3 Оптимальные потоки в транспортных/информационных сетях
59
Рис. 3.16 – Сеть G
Рис. 3.17 – Сеть G
Рис. 3.18 – Сеть G
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Алгоритм нахождения минимального разреза сети.
Процедура «пометок вершин».
Начальное состояние: все вершины не имеют пометок.
Вершине s приписывается пометка.
Всем вершинам x
i
∈
{Г
s
}, для которых дуга (s,x
i
) не насыщена: c
si
> 3
si
при-
сваиваются пометки.
Всем вершинам x
k
∈
{Г
xi
}, для которых дуга (x
i
, x
k
) не насыщена: c
ij
> 3
ij
присваиваются пометки.
В ходе присвоения пометок вершинам сети возможны две ситуации:
1. Удалось присвоить пометку вершине t, из чего следует, что в сети есть путь
от вершины s к вершине t, все дуги которого не насыщены. Следовательно,
60
Глава 3. Экстремальные задачи на графах
поток на сети может быть увеличен за счёт его увеличения на пути s, . . ., t
(с помощью рассмотренного выше алгоритма).
2. Не удалось присвоить пометку вершине t. Следовательно, на сети получен
максимальный поток и для его вычисления возможно построить минималь-
ный разрез.
На рисунке 3.19 приведён результат пометок вершин для рассматриваемой сети:
Рис. 3.19 – Сеть G
Определение дуг минимального разреза.
По результату алгоритма пометок, когда невозможно пометить вершину t (сток),
определяем дуги минимального разреза: это дуги, начала которых находятся в по-
меченных вершинах, а концы — в непомеченных вершинах.
В нашем примере это дуги u
s,1
; u
5,6
; u
2,6
; u
3,t
; u
4,t
(см. рис. 3.20).
Рис. 3.20 – Сеть G
Таким образом, минимальный разрез данной сети T
=
(u
s,1
; u
5,6
; u
2,6
; u
3,t
; u
4,t
).
Вычисление величины максимального потока Ф
max
:
Ф
max
= c
s,1
+
c
5,6
+
c
4,t
+
c
2,6
+
c
3,t
= 12 + 10 + 17 + 12 + 11 = 62.
Допустимый поток максимальной величины на заданной сети G — найден.