ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7086
Скачиваний: 35

Контрольные вопросы по главе 3
61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Контрольные вопросы по главе 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Определение двудольного графа.
2. Определение бихроматического графа.
3. Какой граф называется «паросочетанием»?
4. Свойства бихроматических графов.
5. Какие графы являются 1-хроматическими?
6. Определение транспортной сети.
7. Что является ограничением потока в транспортной сети?
8. Чему равна величина максимального потока в транспортной сети?

Глава 4
ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
4.1 Переключательные функции. Способы задания
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Переключательной функцией (ПФ) f
(x
1
, x
2
, . . ., x
n
) называется од-
нозначное отображение вектора X
=
(x
1
, x
2
, . . ., x
n
), каждая пере-
менная x
i
(x
i
∈ X
) которого принимает значение из множества
{0,1,...,k
i
−
1
}, i = 1,2,...,n в множество f , f ∈ {0,1,...,k
f
−
1
}.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
В случае если k
1
= k
2
= . . . = k
i
= . . . = k
n
= k
f
= k, получаем определение
k-значной функции; в пределе, когда k
= 2 — определение булевой функции.
ПФ можно задавать:
• табличным способом;
• теоретико-графовым;
• аналитическим способом.
Табличными способами являются одномерные и двумерные таблицы. Одно-
мерная таблица, определяющая функцию f
(x
1
, x
2
, . . ., x
n
), имеет размеры:
n
∏
i
=1
k
i
×
(n + 1),
где
n
∏
i
=1
k
i
— количество строк, которые взаимно однозначно соответствуют векторам
X
=
(x
1
, x
2
, . . ., x
n
);(n + 1) — количество столбцов; из них n столбцов взаимно од-
нозначно соответствуют предметным переменным x
1
, x
2
, . . ., x
n
,
(n + 1)-й столбец —
функциональной переменной f .
4.1 Переключательные функции. Способы задания
63
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.1
. . . . . . . . . . . . . . . . . . . . .
Пусть x
1
∈
{0,1,2}; x
2
∈
{0,1}; x
3
∈
{0,1}; f ∈ {0,1,2,3}. Определим переклю-
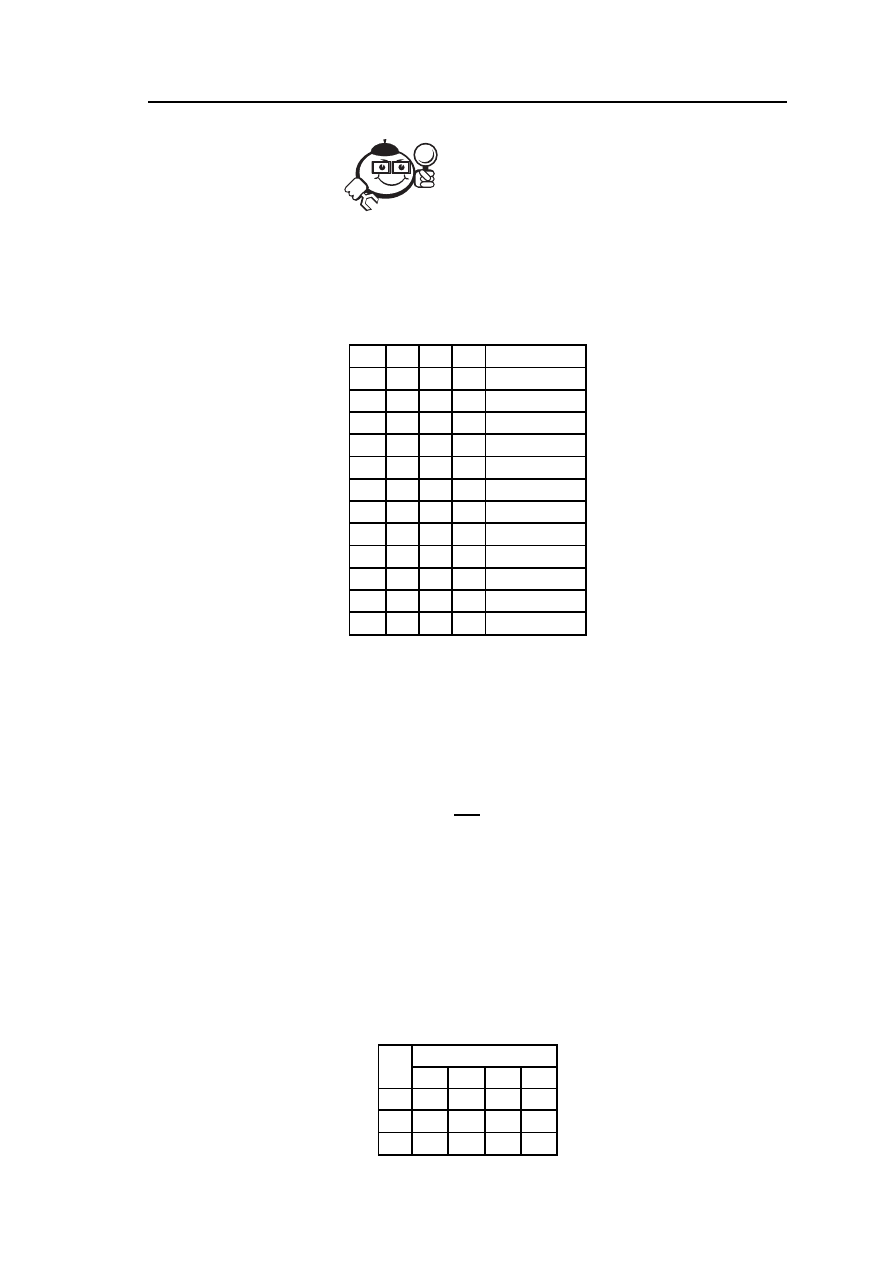
чательную функцию с помощью одномерной таблицы 4.1.
Таблица 4.1 – ПФ — f
(x
1
, x
2
, x
3
)
x
1
x
2
x
3
f
(x
1
, x
2
, x
3
)
1
0
0
0
3
2
0
0
1
3
3
0
1
0
1
4
0
1
1
0
5
1
0
0
2
6
1
0
1
3
7
1
1
0
0
8
1
1
1
1
9
2
0
0
1
10
2
0
1
1
11
2
1
0
0
12
2
1
1
3
Мощность P
(x
1
, x
2
, . . ., x
n
, f
) переключательных функций f (x
1
, x
2
, . . ., x
n
) равна:
P
(x
1
, x
2
, . . ., x
n
, f
) = K
n
∏
i=1
k
i
f
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пусть: если ∀x
i
∈
{0,1} — то для i = 1,2 количество наборов: 2
2
= 4, количество
(мощность) функций: 2
2
2
= 16.
Двумерная таблица, определяющая переключательную функцию f
(x
1
, x
2
, . . ., x
n
),
строится в результате разбиения переменных X
=
(x
1
, x
2
, . . ., x
n
) на два подмноже-
ства: подмножество строчных переменных X
a
и подмножество столбцевых пере-
менных X
b
; в клетке
(i,j) записывается соответствующее значение функции f (x
1
,
x
2
, . . ., x
n
). Такие таблицы называют таблицами Вейча.
Для примера 4.1 таблица Вейча для функции f имеет вид (табл. 4.2):
Таблица 4.2 – Таблица Вейча для ПФ f
(x
1
, x
2
, x
3
)
x
1
x
2
x
3
00
01
10
11
0
3
3
1
0
1
2
3
0
1
2
1
1
0
3

64
Глава 4. Переключательные функции
При теоретико-графовом задании переключательной функции используются
категории (классы):
• мографа G
M
(f ) (модельный граф),
• гиперграфа H
B
(f ),
• графа Кёнига K
(f ),
• гиперкуба H
(f ).
Рассмотрим их.
Задание переключательной функции мографом.
Задание переключательной функции мографом G
M
(f ) связано с одномерной
таблицей (см. табл. 4.1).
Каждая вершина v
i
мографа взаимно однозначно соответствует первичному
терму v
i
↔ x
σ
i
,
σ
i
= 0, 1; f
σ
j
,
σ
j
= 0, 1, 2.
Взаимно однозначно идентифицируем строки одномерной таблицы 0. . .00, 0. . .01, . . .
как 1, 2, 3, . . ., 12.
Вершина f
k
соединяется с вершиной x
k
i
, если f
k
и x
k
i
входят в одинаковые
наборы.
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.2
. . . . . . . . . . . . . . . . . . . . .
Задание переключательной функции f
(x
1
, x
2
, x
3
) мографом (рис. 4.1):
Рис. 4.1 – Мограф переключательной функции f
(x
1
, x
2
, x
3
)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Задание переключательной функции гиперграфом.
Гиперграф H
B
(f ), задающий функцию f (x
1
, x
2
, . . ., x
n
), по существу является
диаграммой Эйлера.
4.1 Переключательные функции. Способы задания
65
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.3
. . . . . . . . . . . . . . . . . . . . .
Фрагмент гиперграфа H
B
(f ), определяющий первые два значения рассмотрен-
ной выше функции f
(x
1
, x
2
, x
3
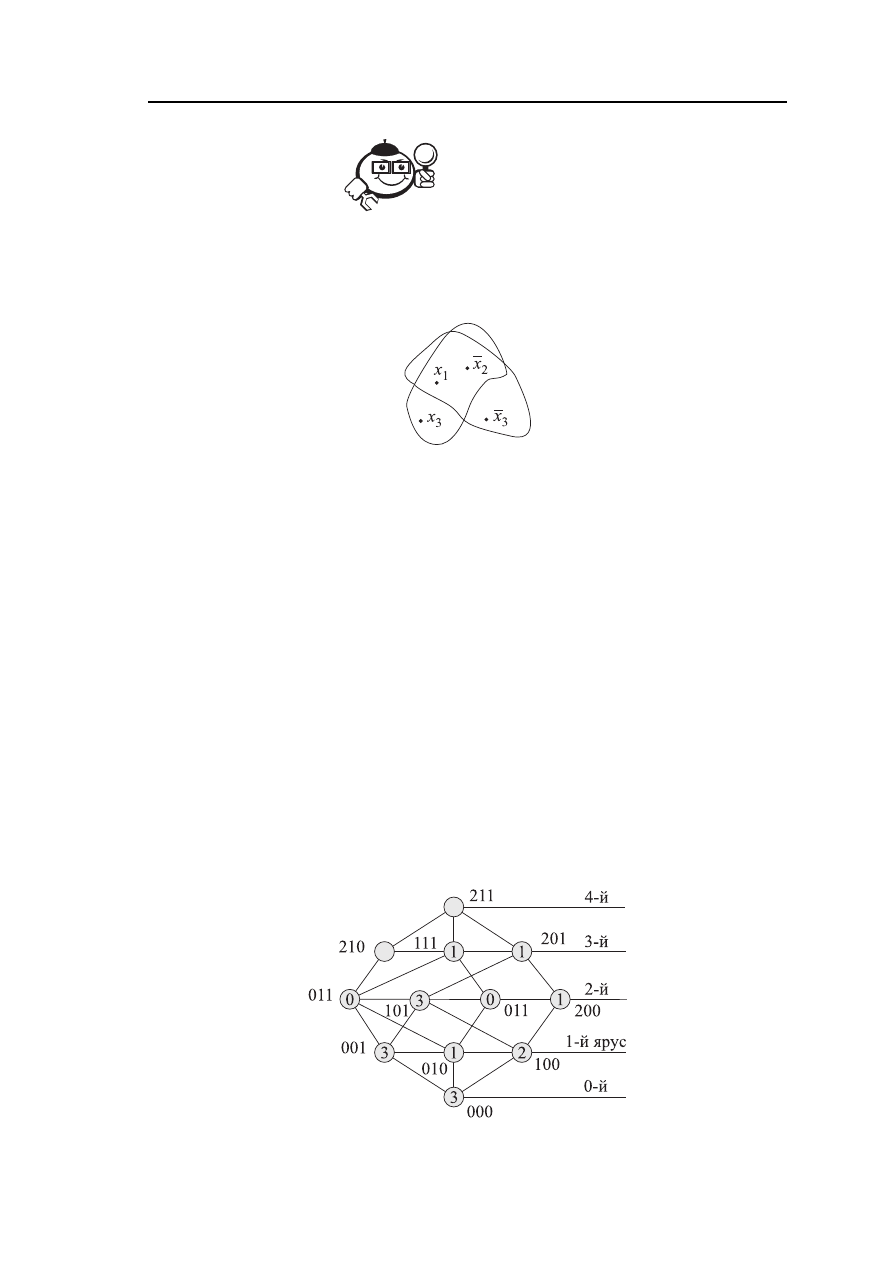
) (табл. 4.1), представлен на рисунке 4.2.
Рис. 4.2 – Фрагмент гиперграфа H
B
(f )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Очевидно, что при большом числе строк соответствующей одномерной табли-
цы геометрическое представление гиперграфа функции не обеспечивает должной
наглядности. В этом случае его целесообразнее представлять модифицированной
матрицей инциденций.
Задание переключательной функции гиперкубом.
Гиперкуб H
(f ) — каждый вектор X функции f (x) взаимно однозначно сопо-
ставляется вершине гиперкуба, и две вершины смежны, если соответствующие
им векторы отличаются в одном и только одном разряде ровно на 1.
Значение переменной называют фазой.
Каждая вершина гиперкуба взвешена значением функции f
(x
1
, x
2
, . . ., x
n
).
В i-м ярусе, если счёт начинать с «0», будут векторы, сумма фаз переменных
которых равна i. Для рассматриваемой функции f
(x
1
, x
2
, x
3
) гиперкуб H(f ) пред-
ставлен на рисунке 4.3.
Рис. 4.3 – Гиперграф ПФ f
(x
1
, x
2
, x
3
), таблица 4.1