Файл: Дискретная математика.pdf

1.3 Булевы выражения

11

Часто все множества на диаграмме размещают внутри квадрата, который пред-

ставляет собой универсум U и обозначается 1. Универсум — это семейство подмно-
жеств множества U .

Если элемент принадлежит более чем одному множеству, то на диаграмме об-

ласти, отвечающие таким множествам, должны перекрываться, чтобы общий эле-
мент мог одновременно находиться в соответствующих областях, как это приведе-
но на рисунках 1.2 и 1.3.

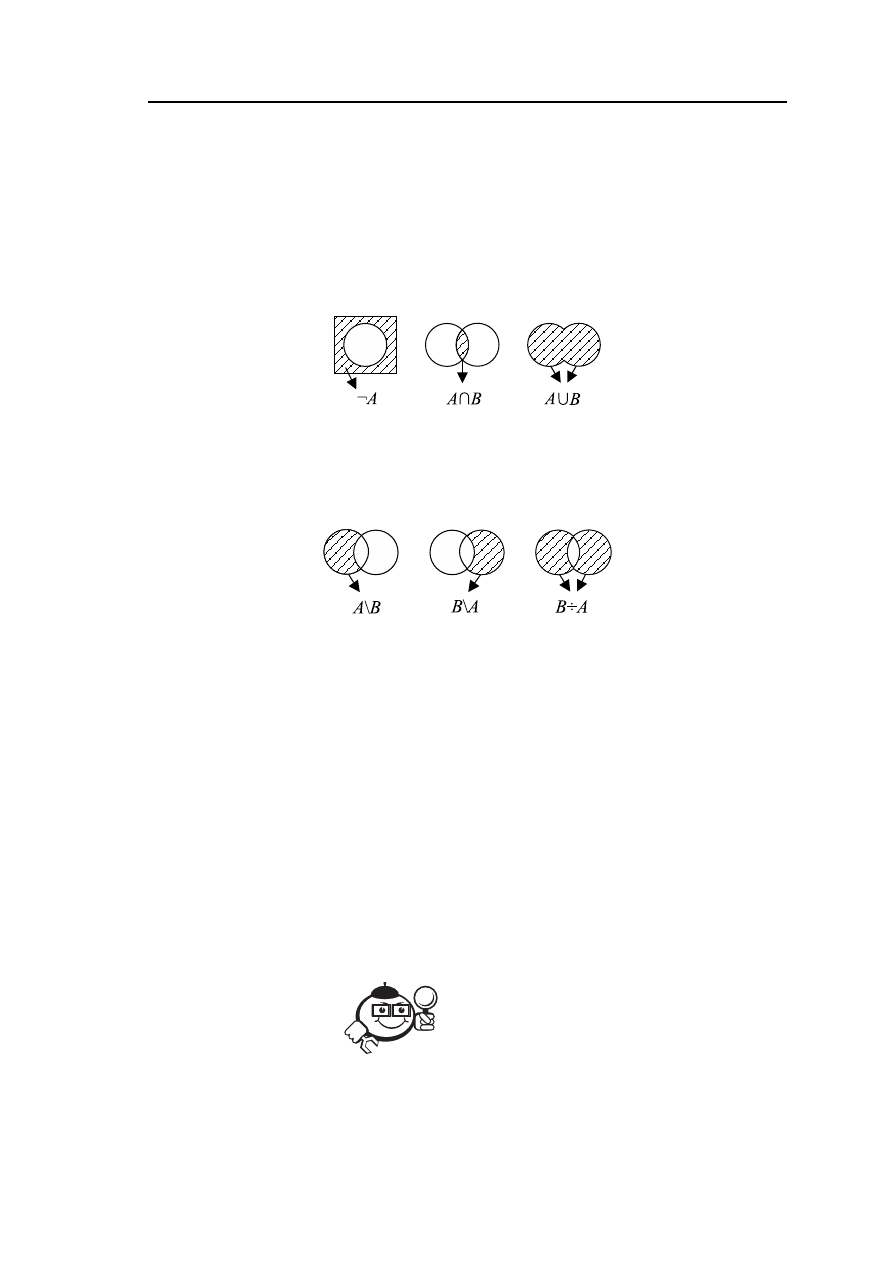
Рис. 1.2 – Диаграммы Эйлера—Венна, отображающие операции над множествами:

¬A — дополнение множества A; A ∩ B — пересечение множеств;

A

∪ B — объединение множеств

Рис. 1.3 – Диаграммы Эйлера—Венна, отображающие операции над множествами:

разность множеств — A

/B и B/A; симметрическая разность множеств — A ÷ B

Относительный размер кругов либо других замкнутых областей не имеет зна-

чения, но лишь их взаимное расположение.

Безусловно, такие диаграммы могут играть в логике лишь ту роль, что чертежи

в геометрии: они иллюстрируют, помогают представить и доказать, но сами ничего
не доказывают.

1.3 Булевы выражения

Объединение, пересечение и дополнение обычно называются булевскими опе-

рациями, составленные из множеств с их помощью выражения — булевыми вы-
ражениями, значение такого выражения — булевой комбинацией входящих в него
множеств, а равенство двух булевых выражений — булевыми тождествами.

. . . . . . . . . . . . . . . . . . . . . .

Пример 1.1

. . . . . . . . . . . . . . . . . . . . .

Примеры булевых тождеств и их представление диаграммами Эйлера—Венна

приведены на рисунках 1.4 и 1.5.

12

Глава 1. Основы теории множеств и отношений

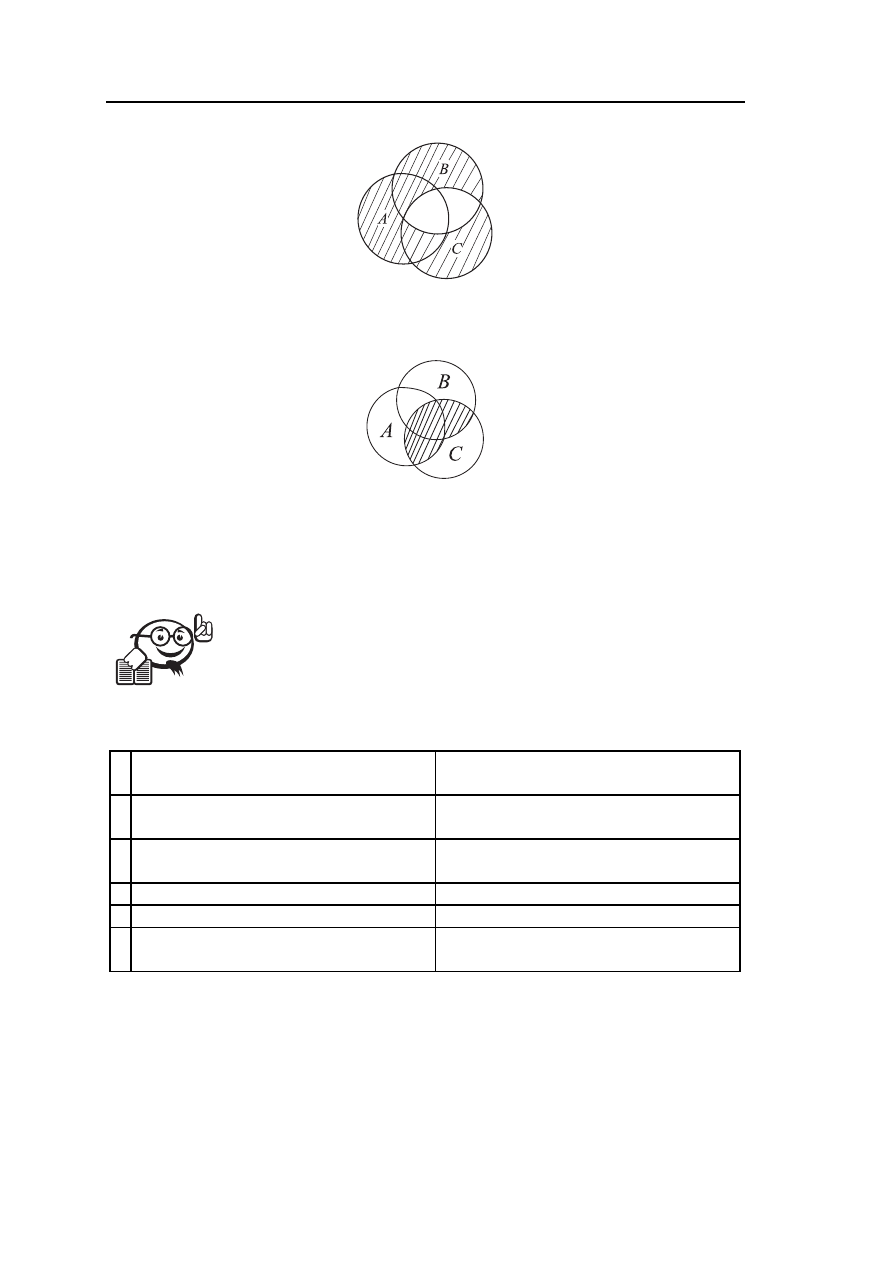
Рис. 1.4 – Булево тождество:

(A ∪ B ∪ C)/(C ∩ B) = (C ÷ B) ∪ (A/(A ∩ B ∩ C))

Рис. 1.5 – Булево тождество:

(A ∩ C) ∪ (B ∩ C) = C/¬(A ∪ B)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для любых подмножеств A, B, C и универсума U выполняются сле-
дующие основные булевские тождества (табл. 1.1):

Таблица 1.1 – Основные булевские тождества

1

A

∪ B = B ∪ A

A

∩ B = B ∩ A

(коммутативность

∪)

(коммутативность

∩)

2

A

∪ (B ∪ C) = (A ∪ B) ∪ C

A

∩ (B ∩ C) = (A ∩ B) ∩ C

(ассоциативность

∪)

(ассоциативность

∩)

3

A

∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

A

∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(дистрибутивность

∪ относительно ∩) (дистрибутивность ∩ относительно ∪)

4

A

∪ ∅ = A

A

∩ U = A

5

A

¬ ∪ A = U

A

¬ ∩ A = ∅

6

A

∪ A = A

A

∩ A = A

(идемпотентность

∪)

(идемпотентность

∩)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Контрольные вопросы по главе 1

13

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Контрольные вопросы по главе 1

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. Дайте определение множества, принадлежащее Георгу Кантору.

2. Напишите: элемент m принадлежит множеству M и элемент m не принад-

лежит множеству M.

3. Назовите операции, которые можно выполнять над множествами.

4. Что является результатом операций над множествами?

5. Для двух множеств A и B задайте операцию «разность».

6. Назовите способы задания множества, если его элементы принадлежат

двум и более множествам.

7. Если два множества не пересекаются, то что является их пересечением?

8. Для множества A

∪ (B ∩ C) запишите тождество:

«дистрибутивность

∪ относительно ∩ ».

9. Для множества A

∩ (B ∪ C) запишите тождество:

«дистрибутивность

∩ относительно ∪ ».

10. Представьте диаграммой Эйлера—Венна множество

(A ∪ B ∪ C)/(C ∩ B).

Глава 2

ТЕОРИЯ ГРАФОВ

2.1 Определение графа

Теория графов оперирует формальными моделями объектов, имеет дело со

свойствами самих графов независимо от того, какова природа объектов, описывае-
мых графами. Использование аппарата теории графов для разработки алгоритмов
конструкторского и технологического проектирования схем ЭВА приводит к повы-
шению эффективности и качества создаваемых объектов.

Понятие графа опирается на понятие множества. Графом можно назвать объ-

ект, состоящий из двух множеств: множества точек и множества линий, которые
соединяют между собой все или часть этих точек.

Множество точек графа обозначается X

= {x

1

, x

2

, . . ., x

n

} и называется множе-

ством вершин. Суммарное число n всех вершин графа называется мощностью мно-
жества X данного графа и обозначается

∣X ∣ = n.

Множество линий, соединяющих любые пары вершин

(x

i

, x

j

), принадлежащих

множеству X , называется множеством рёбер или дуг (если линии имеют направ-
ление) и обозначается:

U

= {u

1

, u

2

, . . ., u

k

, . . ., u

m

},

где u

k

— ребро или дуга графа.

Суммарное число m всех рёбер графа называется мощностью множества рёбер

графа и обозначается

∣U∣ = m.

Таким образом, графом можно считать математический объект, который обо-

значается G

= (X , U) и состоит из множества вершин X и множества рёбер или

дуг U , находящихся между собой в некотором отношении.

В общем случае множество U можно представить в виде:

U

= U ∪ U

0

∪ Ð

→

U ,

где U — подмножество неориентированных линий, для которых не существенен
порядок соединения вершин. Подмножество U называется подмножеством неори-

2.1 Определение графа

15

ентированных рёбер. Каждое ребро u

i

∈ U определяется неупорядоченной парой

вершин x, y, которые оно соединяет и записывается: u

i

= (x, y) или u

i

= (y, x).

Ð→

U — подмножество ориентированных линий, для которых существенен порядок

соединения вершин. Подмножество

Ð→

U называется подмножеством дуг. Каждая ду-

га u

i

∈

Ð→

U определяется упорядоченной парой (кортежем длины два) вершин x

k

, y

l

,

которые дуга u

i

соединяет, и записывается: u

i

= (x

k

, y

l

). Заметим, что u

i

= (x

k

, y

l

)

и u

j

= (u

l

, x

k

) — различные дуги (рёбра) в графе G. U

0

— подмножество линий, каж-

дая из которых выходит и входит в одну и ту же соответствующую этой линии
вершину. U

0

— множество рёбер-петель.

Каждая петля u

i

принадлежит множеству U

0

и определяется упорядоченной

парой вида u

i

= (x

k

, x

k

).

. . . . . . . . . . . . . . . . . . . . . . . . .

Выводы

. . . . . . . . . . . . . . . . . . . . . . . . .

Граф состоит из вершин, которые на плоскости изображаются нумерованными

кружками или точками, и рёбер, изображаемых линиями (со стрелками или без
стрелок), которые соединяют некоторые из этих вершин. Однонаправленное со-
единение ребром двух вершин называется дугой. Двунаправленные или ненаправ-
ленные рёбра называются звеньями. Рёбра, соединяющие вершину саму с собой,
называются петлями.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Рёбра, подходящие к вершине x, называются инцидентными дан-
ной вершине. Соответственно говорят, что вершина x инцидент-
на рёбрам, подходящим к ней.

Количество рёбер, инцидентных вершине x, называется степенью
вершины s

(x).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Вершина x называется изолированной, если её степень s

(x) равна нулю.

Если степени всех вершин равны k, то граф называется регулярным степени k.
Граф является конечным, если он имеет конечное число вершин и рёбер.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Бесконечным графом называется пара

(V(G), E(G)), где V(G) —

бесконечное

множество

элементов,

называемое

вершинами,

а E

(G) — бесконечное семейство неупорядоченных пар элементов

из V

(G), называемых ребрами.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Если оба множества V

(G) и E(G) — счётны, то G называется счётным гра-

фом. Заметим, что наши определения исключают те случаи, когда V

(G) — беско-

нечно, а E

(G) — конечно. Такие объекты являются всего лишь конечными графа-

ми с бесконечным множеством изолированных вершин. Когда E

(G) — бесконечно,