Файл: Дискретная математика.pdf

2.6 Определение числа маршрутов длины «L» на графе

21

Эйлеровой цепью графа называется цепь, содержащая все рёбра
графа. Каждое ребро входит в эйлеров цикл ровно один раз. Граф,
содержащий эйлерову цепь, называется полуэйлеровым графом.
Эйлеровым циклом графа называется цепь, содержащая все рёбра
графа, и каждое ребро входит в цикл ровно один раз. Граф, содер-
жащий эйлеров цикл, называется эйлеровым.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Всякий маршрут (в частности, всякая цепь) графа содержит хотя
бы одну простую цепь, соединяющую ту же пару вершин. Всякий
циклический маршрут нечетной длины содержит простой цикл
нечетной длины. Всякий цикл содержит простой цикл.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Всякий кратчайший маршрут между двумя заданными вершинами
графа есть простая цепь. Всякий цикл наименьшей длины при за-
данной вершине является простым.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.6 Определение числа маршрутов длины «L»
на графе

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Маршрутом

µ

i,j

в графе G

=

(X,U) называется конечная по-

следовательность вершин и рёбер вида —

µ

0, l

=

(x

0

, u

1

, x

1

, u

2

,

x

2

, . . ., x

l

−1

, u

k

, x

l

), где x

0

, x

l

— соответственно начальная и конечная

вершины маршрута

µ

0, l

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Очевидно, в конечном графе G

=

(X,U) можно выделить только конечное чис-

ло маршрутов. Длина маршрута

µ

i,j

равна числу рёбер, которые в него входят.

Часто требуется знать — сколько маршрутов заданной длины в графе G связы-

вает вершину x

i

с вершиной x

j

.

Для определения маршрутов длины q в графе G

=

(X,U) его матрицу смеж-

ности R возводят в степень, равную q. Тогда для каждого значения степени q

=

= 1, 2, . . ., k значение элемента

(r

i,j

)

q

матрицы R

q

определяет количество маршрутов

µ

i,j

длиной, равной значению степени q.

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.1

. . . . . . . . . . . . . . . . . . . . .

Для графа G

=

(X,U) (рис. 2.2) определить количество маршрутов длины,

равной 2.

22

Глава 2. Теория графов

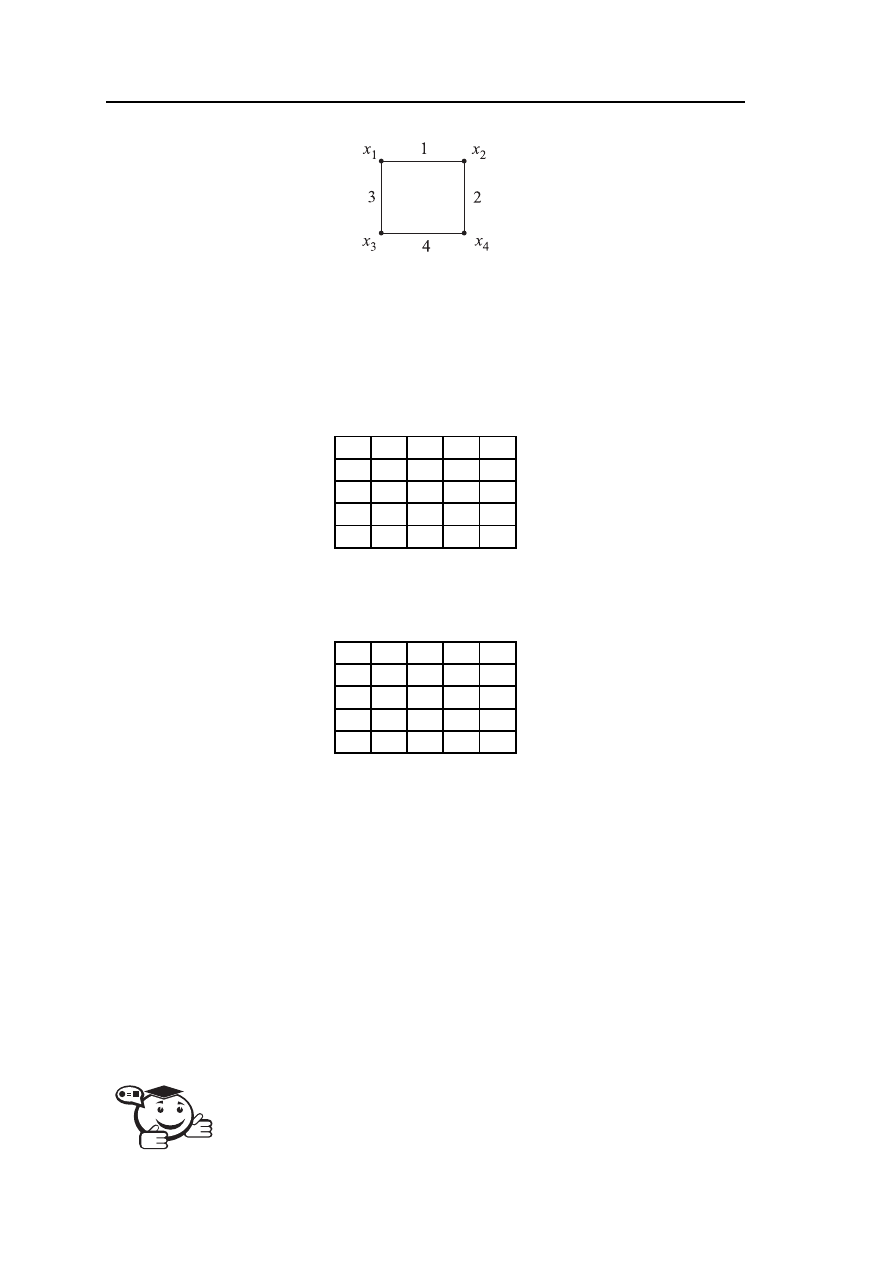
Рис. 2.2 – Граф G

=

(X,U), где X = {x

1

, x

2

, x

3

, x

4

}, U = {1,2,3,4}

Решение:
Зададим граф G его матрицей смежности R. Матрица смежности R имеет вид

таблицы 2.3:

Таблица 2.3 – Матрица смежности R графа G

R

X

1

X

2

X

3

X

4

X

1

0

1

1

0

X

2

1

0

0

1

X

3

1

0

0

1

X

4

0

1

1

0

Возведем матрицу R в степень 2 (табл. 2.4):

Таблица 2.4 – Матрица смежности R графа G в степени 2

R

2

X

1

X

2

X

3

X

4

X

1

2

0

0

2

X

2

0

2

2

0

X

3

0

2

2

0

X

4

2

0

0

2

Значение каждого элемента r

i,j

матрицы R

2

равно числу маршрутов длины 2,

ведущих из вершины x

i

в вершину x

j

.

Например, r

2
3,2

= 2 означает, что в графе имеются два маршрута длины 2, кото-

рые ведут из вершины x

3

в вершину x

2

. Запишем их:

первый маршрут

∶ µ

3,2

= x

3

, 3, x

1

, 1, x

2

;

второй маршрут

∶ µ

3,2

= x

3

, 4, x

4

, 2, x

2

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Операции на графах

Операция «удаление вершины».

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

При удалении вершины удаляются все инцидентные ей рёбра.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.6 Определение числа маршрутов длины «L» на графе

23

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.2

. . . . . . . . . . . . . . . . . . . . .

В графе G

=

(X,U) (рис. 2.3) удалить вершину x

1

.

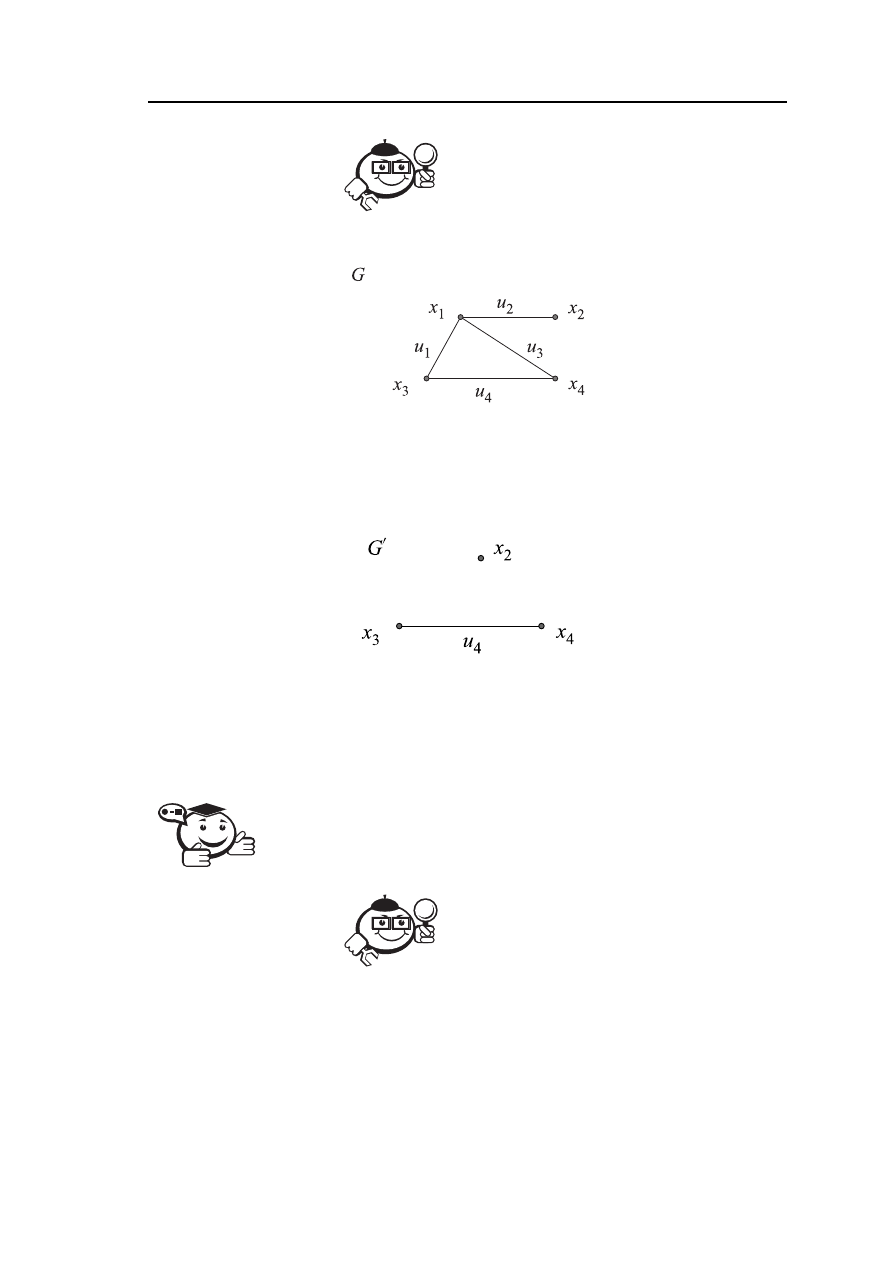
Рис. 2.3 – Граф G

=

(X,U)

Решение:
Результат выполнения данной операции приведён на рисунке 2.4.

Рис. 2.4 – Граф G

′

получен из графа G удалением вершины x

1

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Операция «удаление ребра».

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

При удалении ребра инцидентные ему вершины (концевые) не
удаляются!
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.3

. . . . . . . . . . . . . . . . . . . . .

В графе G

=

(X,U) (рис. 2.3) удалить ребро u

2

.

Решение:
Результат выполнения данной операции — граф G

′′

(рис. 2.5).

24

Глава 2. Теория графов

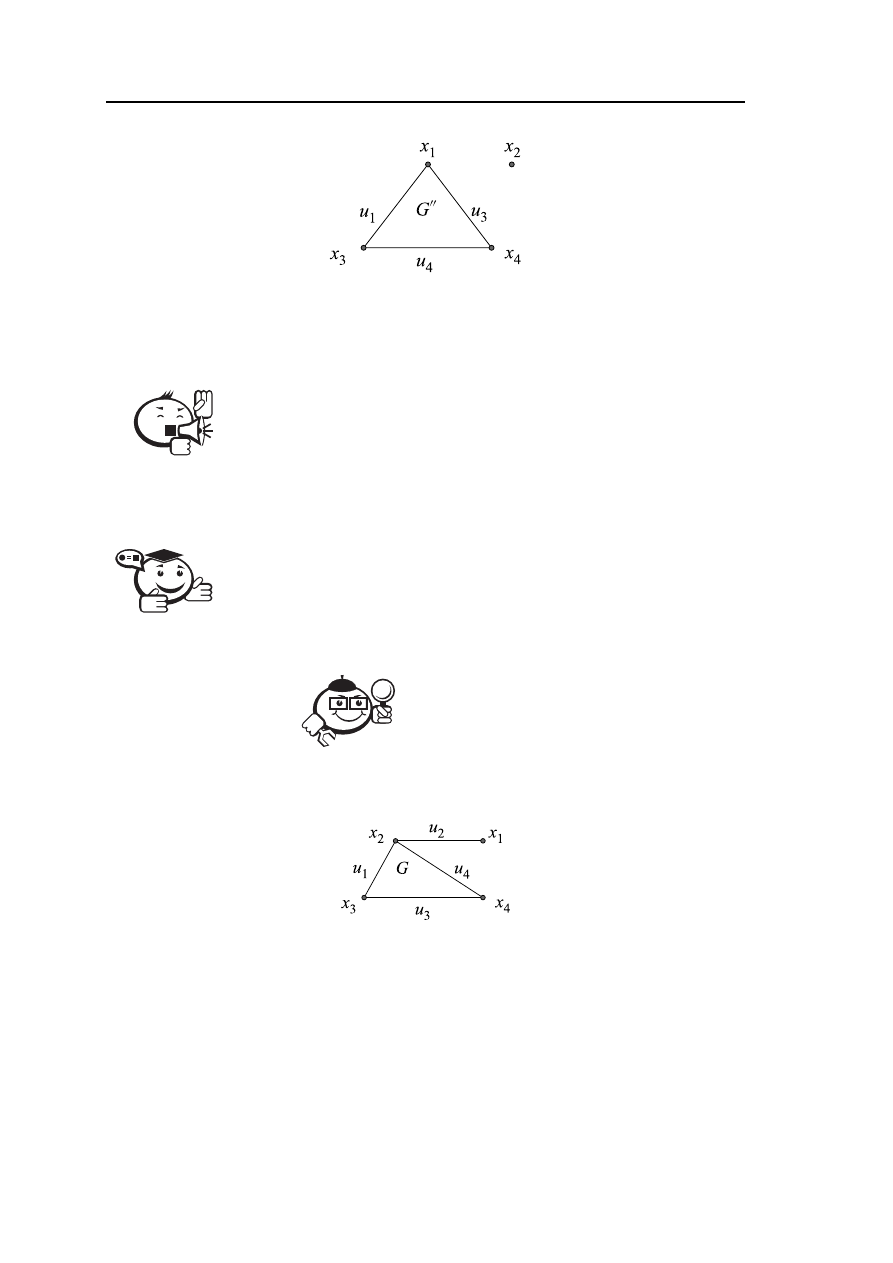
Рис. 2.5 – Граф G

′′

, полученный из графа G удалением ребра u

2

вершины x

1

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Если из графа требуется удалить некоторое множество вершин
и рёбер, то эта процедура сводится к последовательному удалению
каждой вершины отдельно и удалению отдельно каждого ребра.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Замыкание (отождествление) вершин.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для любой заданной пары вершин V

i

, V

j

операция замыкания сво-

дится к отождествлению этих вершин в новую вершину V

k

, при

этом все рёбра, инцидентные вершинам V

i

и V

j

, становятся инци-

дентными вершине V

k

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.4

. . . . . . . . . . . . . . . . . . . . .

На графе G

=

(X,U), представленном на рисунке 2.6, выполнить операцию

«замыкания» вершин x

1

и x

2

.

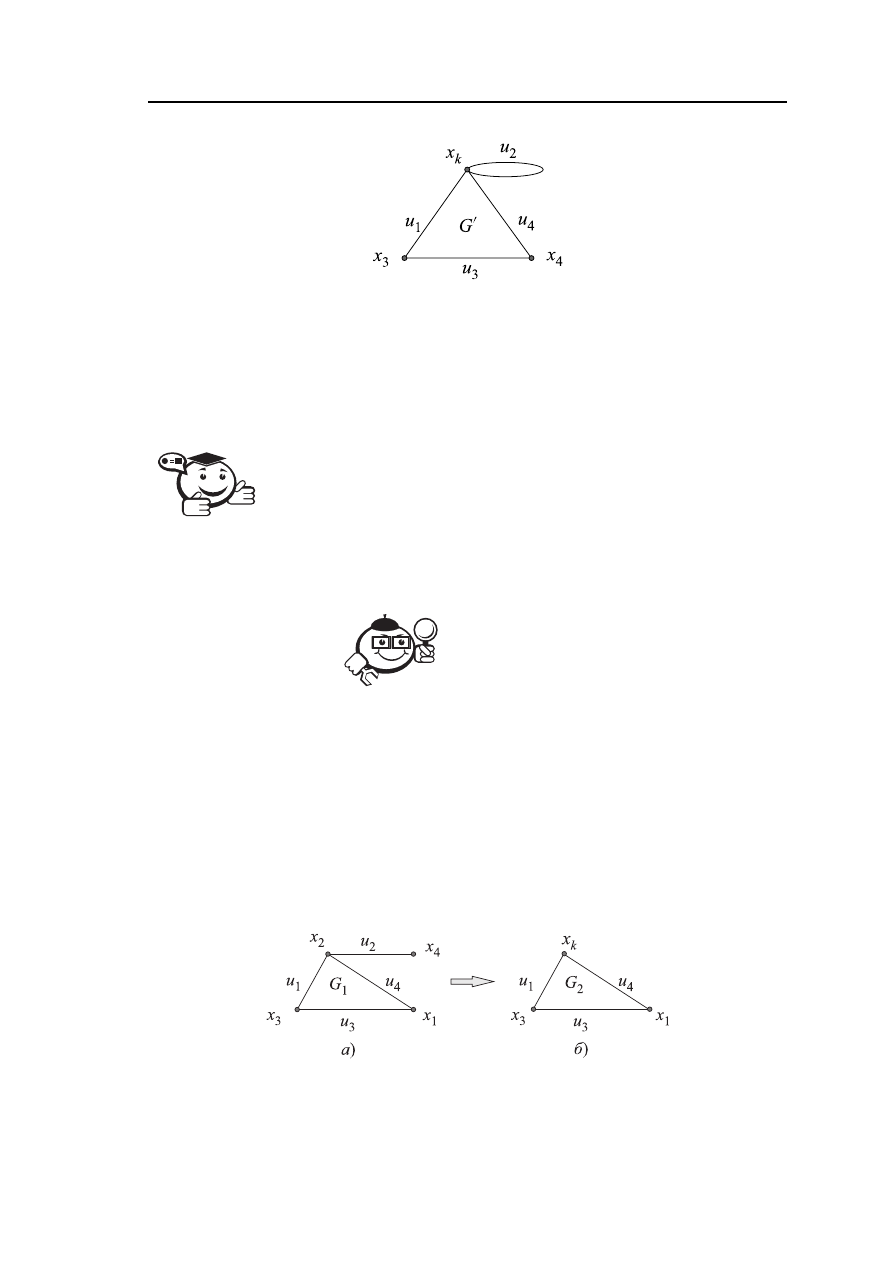
Рис. 2.6 – Граф G

=

(X,U)

Решение:
Граф G

′

, полученный из графа G после «замыкания» вершин x

1

и x

2

, представ-

лен на рисунке 2.7, где вершина x

k

=

(x

1

+ x

2

).

2.6 Определение числа маршрутов длины «L» на графе

25

Рис. 2.7 – Граф G

′

, полученный из графа G c помощью замыкания вершин x

1

и x

2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Стягивание ребра графа.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Результатом операции «стягивания ребра» u

j

в графе G являет-

ся граф G

′

, полученный из графа G удалением из него ребра u

j

и отождествлением его концевых вершин. Говорят, что граф G стя-
гивается к графу H , если граф H можно получить из графа G по-
следовательным стягиванием его рёбер.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.5

. . . . . . . . . . . . . . . . . . . . .

В графе G

=

(X,U) (рис. 2.8, a) выполнить операцию «стягивания» ребра u

2

.

Решение:

Граф G

2

(рис. 2.8, б) получен операцией стягивания ребра u

2

в графе G

1

. В гра-

фе G

2

вершина x

k

=

(x

4

+ x

2

).

Рис. 2.8 – Пример операции стягивания ребра u

2

в графе G

1

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .