ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7074
Скачиваний: 35

16
Глава 2. Теория графов
а V
(G) — конечно, такие объекты являются конечными графами с бесконечным
числом петель или кратных ребер.
Вершинами являются числа 1, 2, . . ., n, а каждое действительное число x, удо-
влетворяющее условию i
< x < i + 1, служит дугой из вершины i в вершину i + 1.
Граф содержит конечное множество вершин и континуум рёбер (дуг).
Вершинами служат все действительные числа, и при фиксированном значении
δ
> 0 вершины x и y соединены ребром (звеном или петлёй) тогда и только тогда,
когда
∣x − y∣ < δ. Каждому значению δ отвечает свой граф, у которого множества
вершин и рёбер оба континуальны.
2.2 Классы графов
Класс орграфов (ориентированных графов). Это граф G
= (X , U), у которого
множество звеньев (неориентированных рёбер) U
= ∅.
Класс неорграфов (неориентированных графов). Это граф G
= (X , U), у кото-
рого множество дуг — пусто.
Класс смешанных графов. Это граф G
= (X , U), у которого есть рёбра-дуги
и рёбра-звенья:
U
⊂ U, Ð
→
U
⊂ U и U ∪ Ð
→
U
⊆ U.
Класс мультиграфов. Мультиграф — это граф G
= (X , U), у которого имеются
параллельные (кратные) рёбра, т. е.
∃x, y ∈ X ∣ x u
k
y, x u
m
y, . . ., x u
p
y, u
k
, u
m
, . . ., u
p
∈ U.
Для некоторых классов графов естественно определяется понятие полного гра-
фа. Полный граф содержит все рёбра, возможные при принадлежности графа дан-
ному классу и при неизменном множестве вершин.
Например, в случае p-графа полнота означает, что при каждой вершине име-
ется ровно p петель (если граф при вершинах содержит петли), а каждая пара
различных вершин связана ровно p-рёбрами (среди них могут быть как звенья, так
и дуги).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Граф общего вида, в котором любые две различные вершины все-
гда смежны, называется полным.
Особо важную роль играют так называемые обыкновенные гра-
фы. Граф этого класса характеризуется следующими четырьмя
свойствами:
1) он конечен;
2) он является неориентированным, т. е. не содержит дуг;
3) он не содержит петель;
4) он не содержит «параллельных» («кратных») рёбер; ина-
че говоря, никакие две его вершины не могут соединяться
более чем одним ребром (звеном).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.3 Способы задания графов
17
Обыкновенный граф — это неориентированный униграф без петель.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Униграф — это граф, в котором смежные вершины связаны только
одним неориентированным ребром.
Дополнением графа L
= (X , U) называется граф L = (X , U
*
) с тем
же множеством вершин X и множеством рёбер U
*
—
U
*
= {x̃y/x, y ∈ X & x ≠ y}/U.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Иначе говоря, это такой граф, в котором две различные вершины смежны тогда
и только тогда, когда они не смежны в исходном графе L.
Рассмотрим ещё одно важное в теории графов понятие — скелет графа.
В случае, когда при исследовании графа L
= (X.U; P) общего вида требует-
ся не полная информация о нём, а лишь знание того, какие пары его различных
вершин смежны, то прибегают к носителю такой информации — скелету графа L,
который обозначим L
= (X , U). Граф L относится к классу обыкновенных графов
с множеством вершин таким же, что и в графе L, и новым множеством рёбер U ,
полученных по следующим правилам:
• если в графе L есть петли, то они удаляются;
• если в графе L есть дуги, то производится дезориентация дуг;
• если в графе L есть кратные рёбра, то они заменяются одним эквивалент-
ным неориентированным ребром.
Остальные рёбра также входят в множество рёбер U .
Таким образом, множество рёбер U состоит из рёбер, полученных из множе-
ства U после выполнения описанных выше правил.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Деревом называется связный ациклический граф.
Граф без циклов называется ациклическим, или лесом.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Способы задания графов
Геометрический способ задания графов
Основой геометрического способа задания графа является рисунок, дающий
визуальное изображение графа. Изображение графа в виде рисунка наглядно рас-
крывает содержательный смысл представляемого объекта. В этом способе верши-
ны графа изображаются точками (кружками), а рёбра — линиями (со стрелками или
без стрелок), концы которых подходят к вершинам графа.
Такое изображение графа ещё называют диаграммой графа.
18
Глава 2. Теория графов
Описание графа через предикат (инцидентор) P
Говорят, что задан граф G
= (X , U, P), если дано множество вершин X , множе-
ство ребер U и трёхместный предикат (инцидентор) P, определяющий, какую пару
вершин x
i
, x
j
, принадлежащих множеству вершин X , соединяет ребро u
k
= (x
i
, x
j
).
Инцидентор P удовлетворяет двум условиям:
1) инцидентор P определён на всех таких упорядоченных тройках элементов
x, u, y, для которых x, y
∈ X и u ∈ U;
2)
∀u ∃x, y {P(x, u, y) & ∀x
′
, y
′
[P(x
′
, u, y
′
) ⇒ (x = x
′
& y
= y
′
) ∨ (x = y
′
& y
= x
′
)]}.
Матричный способ представления графов
Большинство задач автоматизации конструирования схем удобно решать при
использовании матричного способа представления графов. Квадратная таблица R
=
=
∣∣r
i,j
∣∣
n
×n
называется матрицей смежности, если её строки и столбцы соответству-
ют вершинам графа, а элементы r
i,j
образуются по правилу:
• r
i,j
= 1, если вершина x
i
соединена с вершиной x
j
ребром, т. е. x
i
смежна x
j
;
• r
i,j
= 0, в противном случае.
Заметим, что для мультиграфа и смешанного графа задают:
• r
i,j
= p, если вершина x
i
соединена с вершиной x
j
p — числом рёбер;
• r
i,j
= 0, если вершина x
i
не соединена с вершиной x
j
.
Очевидно, что для неорграфов r
i,j
= r
j,i
и для их задания можно использовать
треугольную матрицу R
′
.
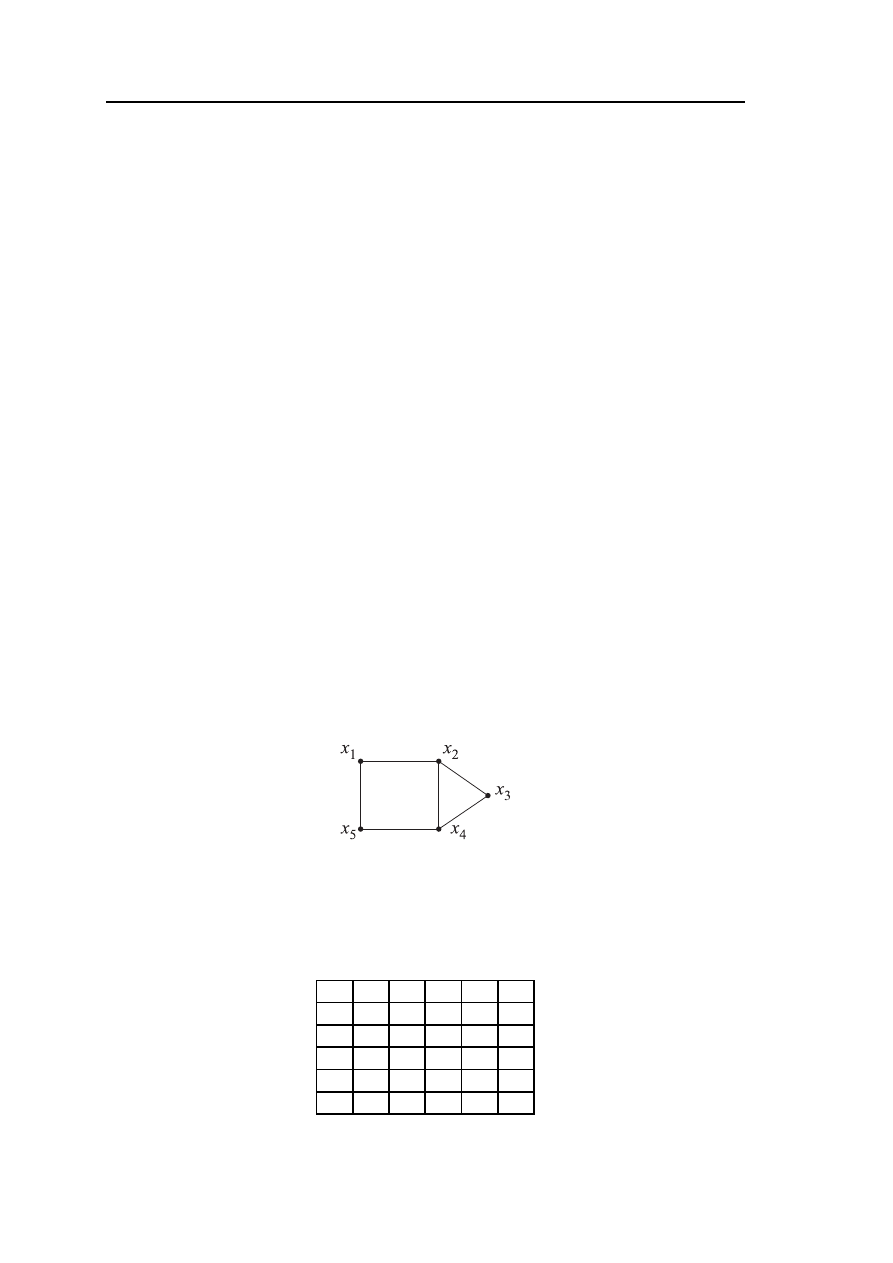
Пример задания графа G (рис. 2.1) матрицей смежности R и треугольной мат-
рицей смежности R
′
.
Рис. 2.1 – Граф G
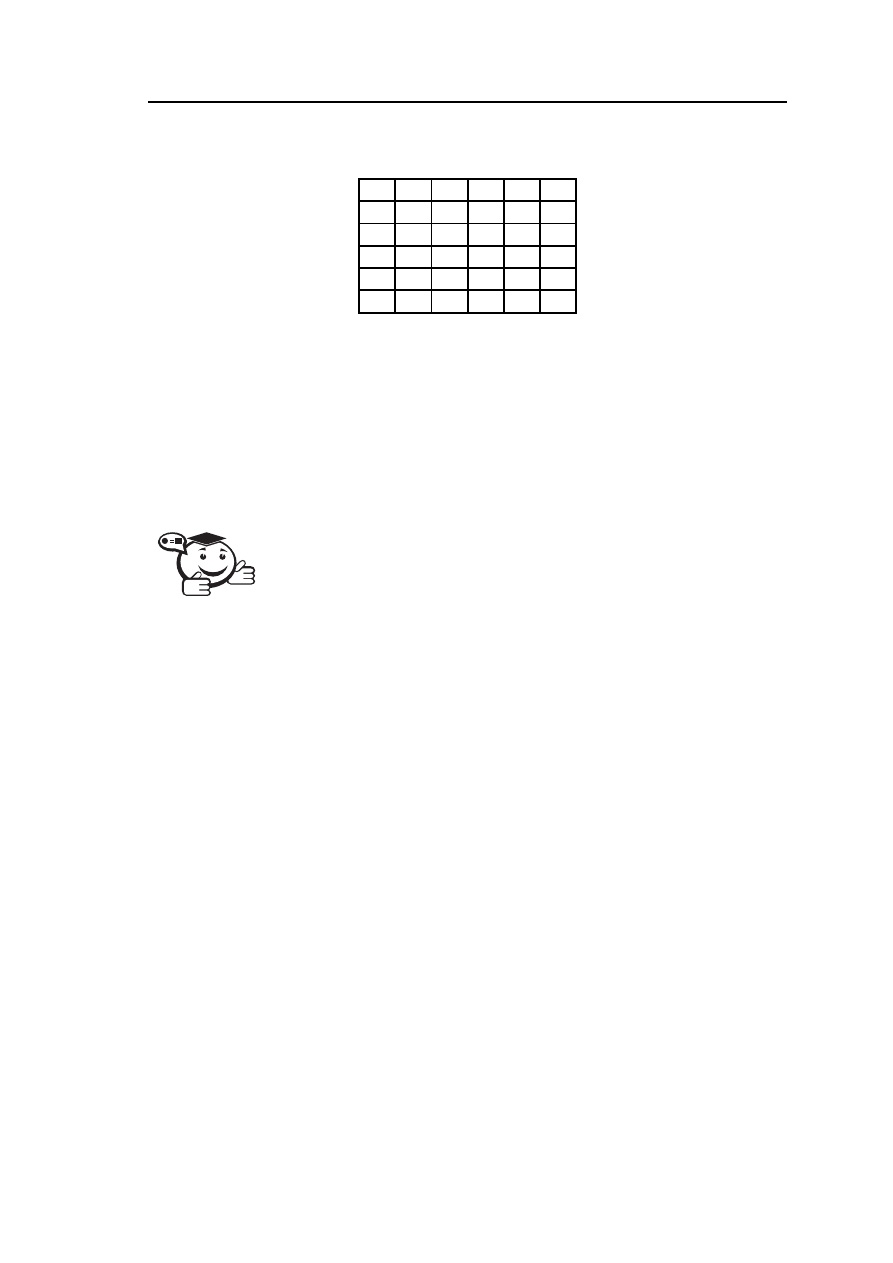
Представление графа G матрицей смежности R имеет вид таблицы 2.1.
Таблица 2.1 – Матрица смежности R графа G
R
X
1
X
2
X
3
X
4
X
5
X
1
0
1
0
0
1
X
2
1
0
1
1
0
X
3
0
1
0
1
0
X
4
0
1
1
0
1
X
5
1
0
0
1
0
Треугольная матрица смежности R
′
графа G имеет вид таблицы 2.2.
2.5 Маршруты, цепи и циклы
19
Таблица 2.2 – Треугольная матрица смежности R
′
графа G
R
′
X
1
X
2
X
3
X
4
X
5
X
1
0
1
0
0
1
X
2
0
1
1
0
X
3
0
1
0
X
4
0
1
X
5
0
Строки и столбцы матрицы R соответствуют вершинам графа. На пересечении
i-й строки и j-го столбца ставится элемент r
i,j
, соответствующий числу рёбер, со-
единяющих вершины x
i
и x
j
. Строки и столбцы матрицы R можно нумеровать чис-
лами натурального ряда, соответствующими индексам помеченных вершин. Пет-
лям в графе соответствуют элементы r
i,i
главной диагонали матрицы R. Преимуще-
ство использования матриц смежности — это простота выполнения преобразований
и операций над графами, как для конструктора, так и для ЭВМ.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Граф можно задавать также матрицей инциденций B, строки ко-
торой соответствуют вершинам графа, столбцы — рёбрам. Элемен-
ты b
i,j
матрицы B для неорграфа могут принимать значения (0 или 1):
• b
i,j
= 1, если ребро u
j
инцидентно вершине x
i
;
• b
i,j
= 0, если ребро u
j
не инцидентно вершине x
i
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Числовые характеристики вершин графа
Каждая вершина x
i
графа G
=
(X,U) имеет числовую характеристику s(x),
которая называется степенью, или валентностью, вершины. Степень вершины s
(x
i
)
это целое, положительное число, равное количеству ребер, инцидентных вершине x
i
.
Для ориентированных графов различают «полустепени исхода» и «полустепе-
ни захода». Это тоже числовые характеристики вершин, соответственно равные
количеству дуг, исходящих из вершины и входящих в вершину.
2.5 Маршруты, цепи и циклы
Рассмотрим такие свойства графов, которые не меняются при произвольной
ориентации звеньев графа, переориентации или дезориентации дуг (всех или неко-
торых).
Мы рассмотрим такие свойства графов общего вида L
=
(X,U;P), которые
полностью определяются предикатом ̃
P
(x,u,y) ⇔ P(x,u,y)∨P(y,u,x), называемым
полуинцидентором (неоринцидентором) графа L.

20
Глава 2. Теория графов
О неорграфе ̃
L
=
(X,U; ̃P) можно сказать, что он получен из L посредством
дезориентации его дуг. В свою очередь, L можно получить из ̃
L ориентацией звеньев.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Конечная последовательность M элементов графа L: M
= x
0
, u
1
,
x
1
, u
2
, x
2
, . . ., x
k
−1
, u
k
, x
k
(k ⩾ 0), для которой истинно высказывание:
P
′
(x
0
, u
1
, x
1
)& P
′
(x
1
, u
2
, x
2
)& ...& P
′
(x
k
−1
, u
k
, x
k
),
называется маршрутом из вершины x
0
в вершину x
k
, или маршру-
том, соединяющим вершину x
0
c вершиной x
k
; в случае x
0
= x
k
име-
ем циклический маршрут при вершине x
0
, или цикл. Число k носит
название длины маршрута M. Иными словами, длина маршрута
равняется числу рёбер, входящих в него.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Заметим, что маршрут — это не просто часть графа, т. к. порядок
его обхода играет существенную роль.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Так, маршрут M
1
:
M
1
= x
k
, u
k
, x
k
−1
, . . . , x
2
, u
2
, x
1
, u
1
, x
0
при k
⩾ 0
не совпадает с написанным выше маршрутом M, хотя и состоит из тех же самых
элементов и с тем же отношением инцидентности.
Виды маршрутов
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Маршрут M
= x
0
, u
1
, x
1
, u
2
, x
2
, . . ., x
k
−1
, u
k
, x
k
называется цепью, если
все рёбра u
1
, u
2
, . . ., u
k
попарно различны. Цепь в случае, если x
0
=
= x
k
, при k
⩾ 1, называется циклом.
Цепь называется простой, если все ее вершины x
p
, x
k
, . . ., x
t
по-
парно различны. В случае, когда x
p
= x
t
, имеем простой цикл,
который, будучи цепью, в то же время не есть простая цепь.
Цепь, в которой начальная и конечная вершины не совпадают, но
есть повторяющиеся вершины, называется циклической.
Гамильтоновой цепью называется простая цепь, содержащая все
вершины графа.
Гамильтоновым циклом графа называется простой цикл, содер-
жащий все вершины графа. Граф, содержащий гамильтонов цикл,
называется гамильтоновым графом.