Файл: Дискретная математика_МУ_Реш.Задач.pdf

26 

Такой же результат можно получить другим, более простым путём. 

Согласно первому условию, лампа горит при A = 0, B = D = 1. Этим 

значениям  соответствует  конъюнкция 

BD

A

,  принимающая  единичное 

значение на двух наборах 0101 и 0111, где включённому реле соответству-

ет неинверсная буква, а выключенному – инверсная. Переменная C в пер-

вом условии не упоминается, поэтому в конъюнкцию её не включаем. Та-

ким образом, получили первую конъюнкцию искомого булева выражения. 

Во втором условии сказано, что лампа горит, если A = B = 1, C = 0. 

Следовательно, конъюнкция имеет вид 

 ,

C

AB

где буквы A и B не содержат 

инверсий,  так  как  им  соответствуют  включённые  реле.  Но  над  буквой  C 

поставлен знак инверсии, поскольку реле C выключено. Это вторая конъ-

юнкция из искомых. 

Аналогично получаем ещё три конъюнкции согласно третьему, чет-

вёртому  и  пятому  условиям: 

D

C

B

A

  (реле  B  включено,  а  все  остальные 

выключены) 

C

B

A

 (реле A выключено, а B и C включены), 

C

B

A

 (реле A 

включено, а B и C выключены). 

Лампа горит, если замкнутой является хотя бы одна из контактных це-

пей, соответствующих этим пяти конъюнкциям. Следовательно, все найден-

ные конъюнкции соединяем знаками дизъюнкции. В результате получаем: 

.

C

B

A

BC

A

D

C

B

A

C

AB

BD

A

f











Нанесём  это  выражение  на  карту  Вейча  и  минимизируем.  Получим 

тот же результат, что и в случае табличного способа.  

Строим контактную схему (рис. 9). На рис. 9 инверсной буквой обо-

значен  нормально  замкнутый  контакт,  неинверсной  –  нормально  разо-

мкнутый. 

Согласно изображению схемы, она содержит два нормально замкну-

тых контакта и два – нормально разомкнутых. 

Ответ: 2, 2.  

27 

ТЕМА 8. КОМБИНАЦИОННЫЕ СХЕМЫ 

Эта  тема  похожа  на  предыдущую.  Отличие:  рассматривается  элек-

тронная  интерпретация  булевых  формул.  Для  решения  задачи  о  синтезе 

комбинационного преобразователя необходимо вникнуть в такие понятия, 

как  логические  элементы,  триггер  типа  RS,  триггерный  регистр,  весовые 

и невесовые  двоичные  коды,  таблица  истинности,  описывающая  работу 

преобразователя кода. 

В учебном пособии показан синтез комбинационного преобразовате-

ля,  на  вход  которого  поступают  четырёхразрядные  двоичные  коды, 

а на выход – пятиразрядные (п. 7.8). В данной же задаче рассматривается 

простейший случай преобразователя: он  содержит  четыре входа и  только 

один выход. Логика работы преобразователя задаётся булевой функцией f, 

представленной  в  СДНФ,  т. е. перечислением входных кодов,  на которые 

схема реагирует высоким уровнем выходного сигнала. Кроме того, приво-

дится перечень запрещённых кодов, которые не будут подаваться на вход 

схемы. Эти коды для функции f являются неопределёнными состояниями. 

Прежде чем строить логическую схему, функцию необходимо мини-

мизировать. Построение комбинационной схемы проиллюстрируем на сле-

дующем примере. 

Пример. Построить комбинационную схему на основе минимальной 

ДНФ следующей функции: 

f = (1, 4, 5, 11, 13, 14), 

[2, 3, 7, 10, 15]. 

В квадратных скобках указаны неопределённые состояния. 

Определить числа a, b и c, где 

a – число элементов И, содержащих по два входа; 

b – число элементов И, содержащих по три входа; 

c – число элементов И, содержащих по четыре входа. 

28 

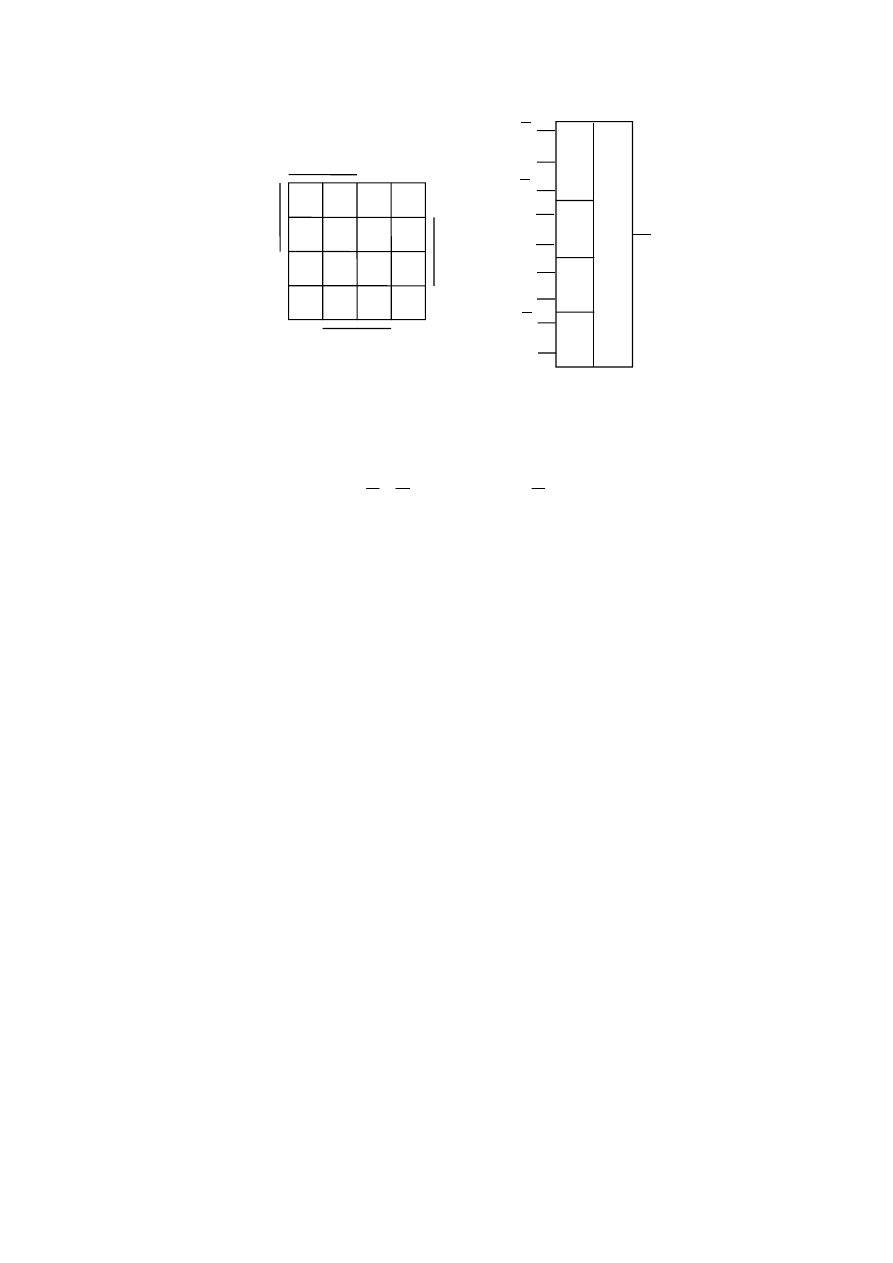
Решение. Находим минимальную ДНФ по карте Вейча (рис. 10): 

.

D

A

BD

AC

C

B

A

f









Соответствующая схема приведена на рис. 11. В этой схеме три эле-

мента  И  по  два  входа  каждый.  Следовательно, a  =  3.  Кроме  того,  схема  

содержит  один  элемент  И  с  тремя  входами.  Следовательно,  b  =  1.  Четы-

рёхвходовых элементов в схеме нет. Следовательно, c = 0. 

Ответ: 3, 1, 0. 

Рис. 11 

1 

f 

A 

B 

C 

A 
C 
B 

D 

A 

D 

& 

& 

& 

& 

Рис. 10 

A 

B 

C 

D 

1 

1 

1 

1 

× 

1 

× 

× 

× 

× 

1 

29 

ТЕМА 9. ФУНКЦИОНАЛЬНО ЗАМКНУТЫЕ КЛАССЫ 

Эти классы составляют основу теоремы Поста. В пособии (п. 8.7) она 

сформулирована следующим образом: 

Система булевых функций называется функционально полной, если 

она содержит хотя бы одну функцию: 

1) не сохраняющую константу 1; 

2) не сохраняющую константу 0;  

3) несамодвойственную;  

4) нелинейную; 

5) немонотонную. 

Прикладное  значение  теоремы  Поста  состоит  в  том,  что  она  даёт 

критерий,  позволяющий  ответить  на  вопрос:  всякую  ли  булеву  функцию 

можно  представить  в  виде  комбинационной  схемы,  используя,  например, 

только три элемента, описываемых булевыми функциями f

1

, f

2

 и f

3

. Чтобы 

ответить на этот  вопрос,  все  три функции необходимо проверить на при-

надлежность  к  замкнутым  классам.  Например,  если  все  они  сохраняют 

константу  1,  то  построить  на  их  основе  схему,  реализующую  функцию, 

не сохраняющую  единицу,  невозможно.  Если  все  они  являются  монотон-

ными, то построить схему на основе функции, являющейся немонотонной, 

не удастся. То же самое относится и к остальным трём классам. 

При определении функциональной полноты по Посту главным явля-

ется  выявление  принадлежности  исследуемых  функций  замечательным 

классам: монотонным, линейным, самодвойственным, сохраняющим нуль, 

сохраняющим  единицу.  После  выполнения  этих  операций  остаётся  один 

шаг  –  определить  по  теореме  Поста,  является  ли  функционально  полной 

исследуемая система булевых функций.  

Но в данной работе контрольная задача представлена в упрошённом 

виде.  Во-первых,  исследуемая  система  состоит  лишь  из  одной  функции, 

30 

а во-вторых, её требуется исследовать только на принадлежность к функ-

ционально замкнутым классам. 

Чтобы правильно решить контрольную задачу данной темы, необхо-

димо ознакомиться со всеми подразделами девятой главы учебного посо-

бия,  обратив  особое  внимание  на  признаки  функциональной  замкнутости 

булевых функций. 

Как  решать  задачу  на  тему  «Функционально  замкнутые  классы», 

проиллюстрируем на примере. 

Пример. 

Является ли функция 

f = (2, 3, 4, 5, 6, 7, 8, 9, 10, 11) 

1) монотонной? 

2) линейной? 

3) самодвойственной? 

4) сохраняющей нуль? 

5) сохраняющей единицу? 

Решение. Условимся обозначать ответ «да» единицей, а «нет» – ну-

лём. Тогда результат решения данной задачи представится упорядоченной 

последовательностью пяти двоичных знаков. Решаем задачу: 

1)  нанесём  функцию  на  карту  Вейча  (здесь  она  не  приводится) 

и найдём минимальную ДНФ: 

.

C

A

B

A

B

A

f







Так как в минимальной ДНФ содержатся инверсии, то функция не вхо-

дит  в  класс  монотонных.  Ответ  относительно  монотонности:  0  (т.  е.  «нет», 

что обозначает: заданная функция не является монотонной);