Файл: Дискретная математика_МУ_Реш.Задач.pdf

21 

Решение. Строим карту Вейча (рис. 5). По карте находим минималь-

ную ДНФ: 

.

CD

C

A

D

B

A

f







Находим числа a, b и c: 

1) в минимальной ДНФ 7 вхождений переменных (т. е. общее число 

букв), следовательно, a = 7;  

2) в минимальной ДНФ три слагаемых, следовательно, b = 3; 

3)  так  как  слагаемых  3,  то  знаков  дизъюнкции  2,  следовательно,            

c = 2. 

Ответ: 7, 3, 2. 

Рис. 5 

A 

B 

C 

D 

× 

1 

× 

1  1 

× 

1 

1  × 

× 

1 

22 

ТЕМА 6. МИНИМИЗАЦИЯ КОНЪЮНКТИВНЫХ 

НОРМАЛЬНЫХ ФОРМ 

Минимизация  КНФ  на  основе  исходной  ДНФ  осуществляется  в  ос-

новном так же, как и в случае ДНФ. Отличие состоит лишь в том, что до-

бавляются  две  операции  инвертирования:  первая  из  них  осуществляется 

при помощи карты Вейча, а вторая – с применением теоремы де Моргана. 

Если  процедуру  минимизации  КНФ  представить  в  виде  последова-

тельности действий, то получим следующий список: 

1) заданную функцию f наносим на карту Вейча; 

2) карту Вейча, на которую нанесена заданная функция f, инвертиру-

ем: т. е. заменяем на ней все единицы нулями, а все нули единицами, при 

этом  неопределённости  оставляем неизменными,  так  как  неопределённые 

состояния не инвертируются. В результате получим функцию 

f

; 

3) находим минимальную ДНФ функции 

f

; 

4) по теореме де Моргана инвертируем минимальное выражение 

f

. 

Получим минимальную КНФ. 

Проиллюстрируем эти действия на следующем примере. 

Пример.  Найти  минимальную  конъюнктивную  нормальную  форму 

следующей  булевой  функции,  представленной  в  СДНФ  (в  квадратных 

скобках приведены неопределённые состояния): 

f = (2, 4, 7, 8,13), [0, 1, 3, 9, 10, 12, 14]. 

Определить числа a и b, где 

a – число букв в минимальной КНФ; 

b – число знаков дизъюнкции в минимальной КНФ. 

Решение. 

1. Наносим заданную функцию f на карту Вейча (рис. 6). 

2. Строим карту для функции 

f

 (рис. 7). 

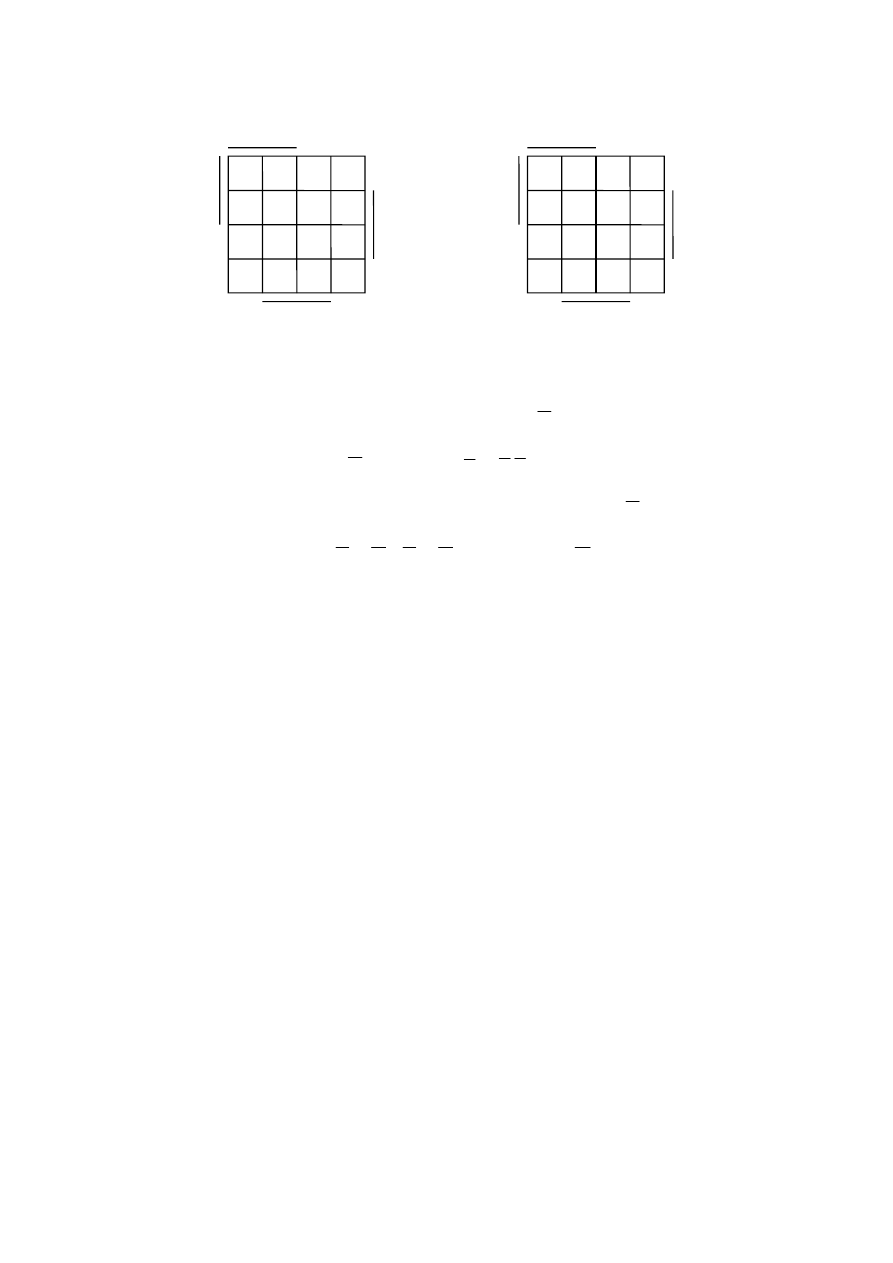
23 

3. Находим минимальную ДНФ функции 

f

: 

.

f

AC BCD ACD







4. Инвертируем по теореме де Моргана выражение 

f

: 

.)

)(

)(

(

D

C

A

D

C

B

C

A

f













Получили минимальную КНФ. Находим числа a и b. Всего в мини-

мальной  КНФ  8  букв,  следовательно,  a  =  8.  В  скобочных  выражениях 

имеются знаки дизъюнкции. Всего их 5, следовательно, b = 5. 

Ответ: 8, 5. 

Рис. 6 

A 

B 

C 

D 

× 

1 

1 

1 

1 

× 

1 

× 

× 

× 

× 

× 

Рис. 7 

A 

B 

C 

D 

× 

1 

1 

1 

× 

× 

× 

× 

× 

× 

1 

24 

ТЕМА 7. КОНТАКТНЫЕ СТРУКТУРЫ 

С математической точки зрения эта тема относится к прикладной ал-

гебре  логики.  Её  основу  составляет  контактная  интерпретация  булевых 

формул. 

Суть задачи на тему «Контактные структуры» состоит в следующем. 

Требуется  построить  схему,  состоящую  из  четырёх  реле,  для  управления 

осветительной лампой накаливания. При этом перечисляются все условия, 

при каких состояниях реле лампа горит и при каких не горит. Схема долж-

на быть минимальной по числу реализующих её контактов. 

Решение задачи сводится к выполнению следующих действий: 

1) по словесному описанию работы схемы составить булеву функцию; 

2) найти её минимальную ДНФ; 

3) по минимальной ДНФ изобразить контактную схему; 

4) по схеме определить, сколько в ней нормально замкнутых и сколько 

нормально разомкнутых контактов; 

5)  полученные  в  предыдущем  пункте  два  числа  являются  ответом 

к задаче. 

Для решения задачи необходимо усвоить технические понятия, такие 

как «электромагнитные реле», «тумблеры», «кнопки»; «нормально замкну-

тые и нормально разомкнутые контакты»; «параллельно-последовательные 

и мостиковые контактные структуры». 

Пример. На основе минимальной ДНФ булевой функции построить 

контактную схему для управления электрической лампой при помощи че-

тырёх реле A, B, C, D. Лампа горит, если выполняется хотя бы одно из пяти 

условий: 

1) включены реле B и D, а реле A выключено; 

2) включены реле A и B, а реле C выключено; 

25 

3) включено реле B, а реле A, C и D выключены; 

4) включены реле B и C, а реле A выключено; 

5) включено реле A, а реле B и C выключены. 

Определить, сколько в контактной схеме нормально замкнутых кон-

тактов, сколько нормально разомкнутых. 

Решение.  Сначала  рассмотрим  решение 

табличным  методом.  Представим  условия 

в виде  таблицы  (табл.  1).  В  первой  строке  за-

писано 0 1 

 1, где нуль согласно условию обо-

значает, что реле A выключено, а единицы го-

ворят о том, что реле B и  D включены. Значение  C отмечено звёздочкой. 

Её можно заменить нулём или единицей. Если заменим нулём, то получим 

пятый минтерм, если единицей, то получим минтерм 7. Числа 5 и 7 запи-

сываем  в  колонке  «Минтермы»  первой  строки.  Точно  так  же  заполняем 

и остальные строки колонки «Минтермы». Дизъюнкция всех этих минтер-

мов  есть  СДНФ  искомой  функции,  описывающей  работу  контактной 

структуры: 

f = (4, 5, 6, 7, 8, 9, 12, 13).

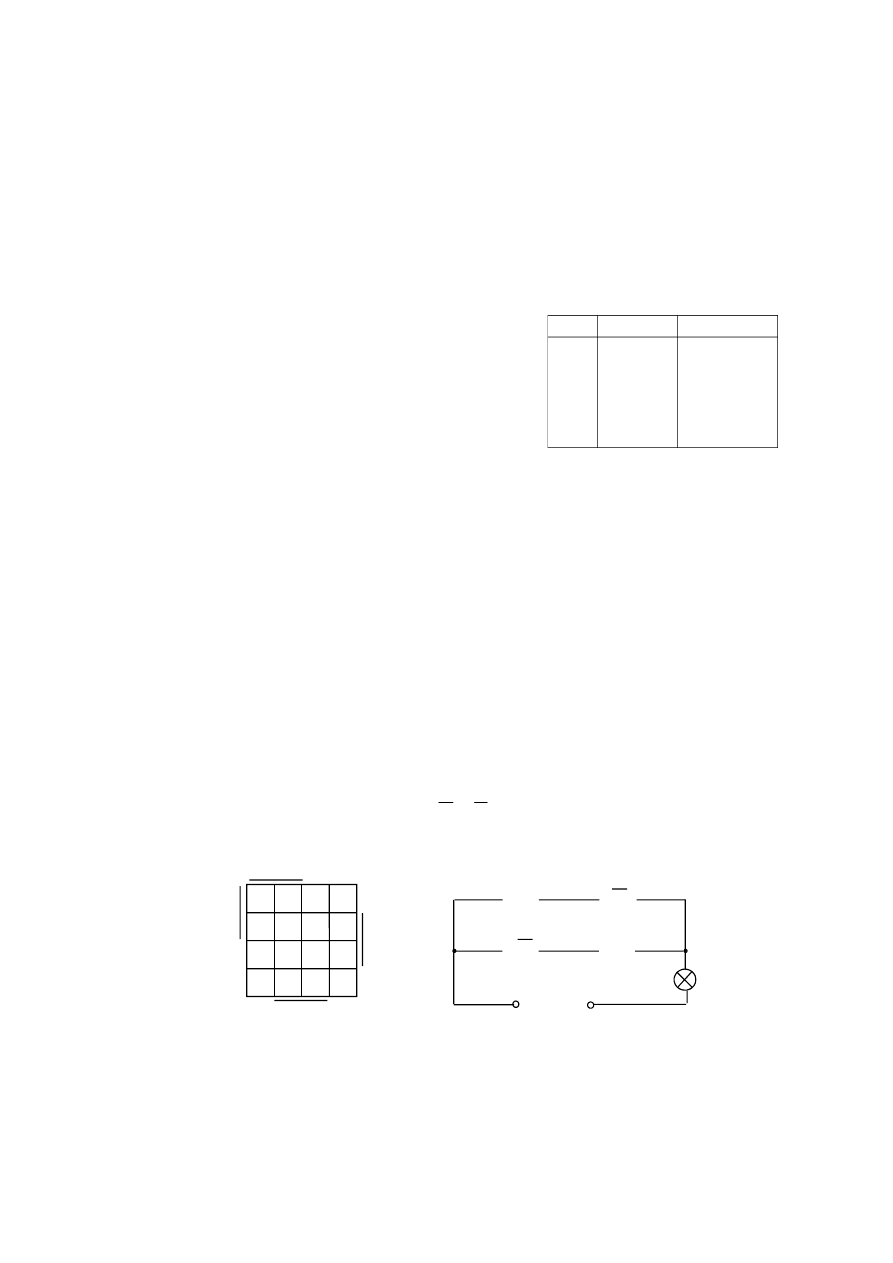
Нанесём это выражение на карту Вейча (рис. 8) и минимизируем: 

.

B

A

C

A

f





Рис. 9 

220 В 

H 

A 

C 

A 

B 

Рис. 8 

1 

1 

1 

1 

1 

1 

1 

1 

D 

A 

B 

C 

   Таблица 1 

Дес.  A B C D  Минтермы 

1 
2 
3 
4 
5 

0  1  

  1 

1  1  0  

  

0  1  0  0 
0  1  1  

 

1  0  0  

 

5, 7 

12, 13 

4 

6, 7 
8, 9