ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 3693
Скачиваний: 93
16
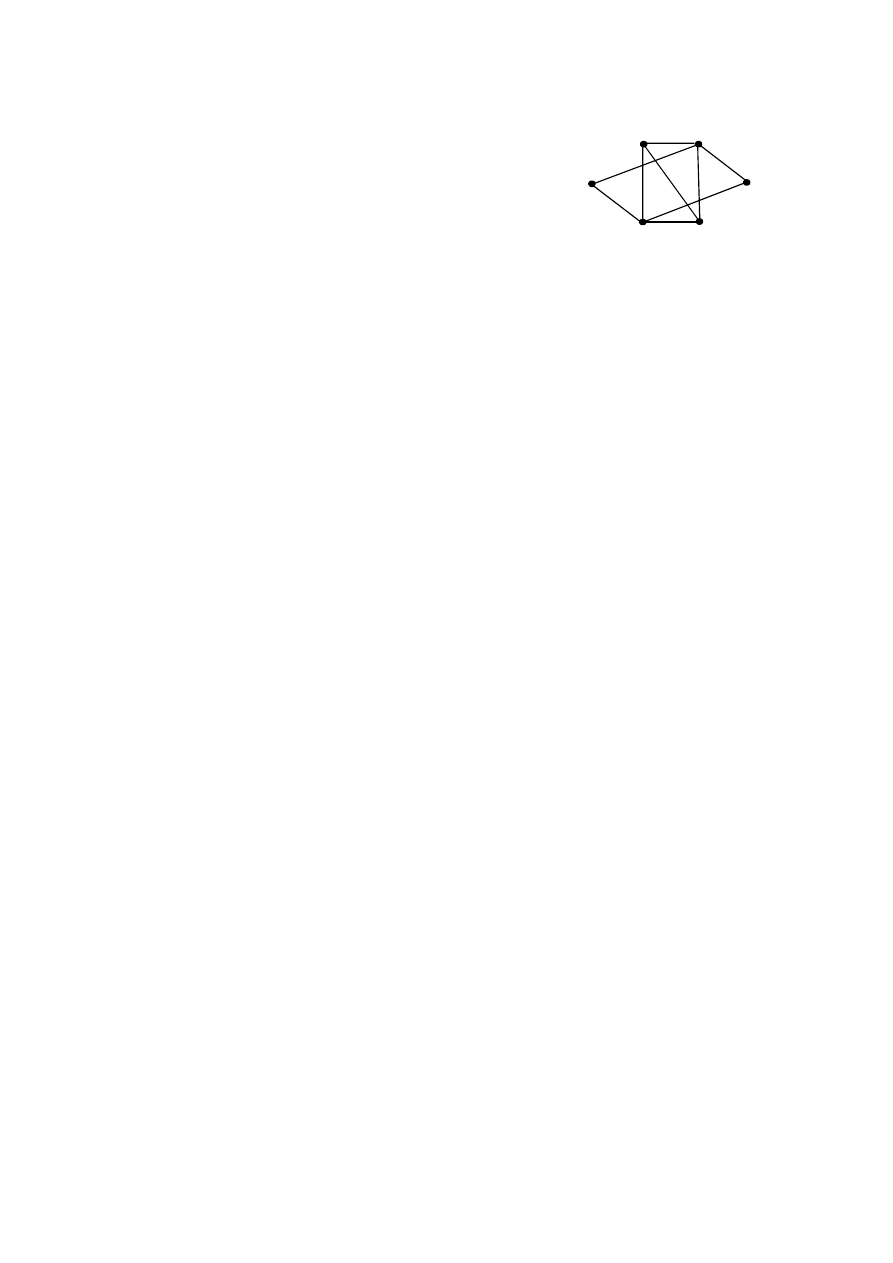
Рис. 1
1
2
3
6
5
4
Этап 1. Согласно рисунку 1, из вершины
1 можно выйти двумя вариантами: 1-3, 1-4.
На этом первый этап заканчивается.
Этап 2. Продолжаем движение по пути
1-3. Из вершины 3 существует четыре варианта
движения: 1-3-1, 1-3-2, 1-3-5, 1-3-6. Из них цепь
1-3-1 удаляем, так как в ней вершина 1 повторяется. Из оставшихся цепь
1-3-6 является искомой. Её также удаляем. Продолжаться могут только две
цепи 1-3-2 и 1-3-5. Точно такой же случай при движении по пути 1-4: цепь
1-4-1 удаляем из-за повтора вершины 1. Цепь 1-4-6 удаляем, так как она
является искомой. Продолжаться могут только две цепи: 1-4-2 и 1-4-5.
Таким образом, на втором этапе найдены две искомые простые цепи,
содержащие по два ребра: 1-3-6 и 1-4-6, а также четыре цепи, которые про-
должаются: 1-3-2, 1-3-5, 1-4-2 и 1-4-5.
Этап 3. Действуем, как и в предыдущем случае. Берём цепь 1-3-2.
Из вершины 2 можно выйти двумя путями (в вершину 3 не возвращаемся).
Получим две продолжающиеся цепи: 1-3-2-4 и 1-3-2-5. Цепь 1-3-5 также
даёт две продолжающиеся цепи: 1-3-5-2 и 1-3-5-4. То же самое относится
к цепи 1-4-2, продолжая которую получаем цепи 1-4-2-3 и 1-4-2-5, а также
к цепи 1-4-5, дающей продолжения: 1-4-5-2 и 1-4-5-3.
Таким образом, на третьем этапе получено 8 продолжающихся цепей
и ни одной из искомых:
1-3-2-4, 1-3-2-5, 1-3-5-2, 1-3-5-4, 1-4-2-3, 1-4-2-5, 1-4-5-2, 1-4-5-3.
Этап 4. Цепь 1-3-2-4 имеет продолжения: 1-3-2-4-5 и 1-3-2-4-6.
Из них вторая цепь – искомая. У цепи 1-3-2-5 только одно продолжение:
1-3-2-5-4. Далее получаем:
1-3-5-2-4, 1-3-5-4-2, 1-3-5-4-6, 1-4-2-3-5, 1-4-2-3-6, 1-4-2-5-3, 1-4-2-5-6,
1-4-5-2-3, 1-4-5-3-2, 1-4-5-3-6.

17
Таким образом, на четвёртом этапе получено 5 искомых цепей длины
4, т. е. содержащих по 4 ребра:
1-3-2-4-6, 1-3-5-4-6, 1-4-2-3-6, 1-4-2-5-6, 1-4-5-3-6,
и 8 продолжающихся
1-3-2-4-5, 1-3-2-5-4, 1-3-5-2-4, 1-3-5-4-2,
1-4-2-3-5, 1-4-2-5-3, 1-4-5-2-3, 1-4-5-3-2.
Этап 5. Четыре цепи не имеют продолжения: 1-3-2-4-5, 1-3-5-4-2,
1-4-2-3-5, 1-4-5-3-2. Удаляем их, так как они не могут привести к вершине
6. Остальные четыре цепи продолжаются. Они оканчиваются вершиной 6
и содержат по пять рёбер каждая:
1-3-2-5-4-6, 1-3-5-2-4-6, 1-4-2-5-3-6, 1-4-5-2-3-6.
Таким образом, в заданном графе (рис. 1) вершины 1 и 6 соединяют
следующие простые цепи:
1) две цепи длины 2, т. е. содержащие по два ребра;
2) ни одной цепи длины 3;
3) четыре цепи длины 4;
4) четыре цепи длины 5.
Ответ: 2, 0, 4, 4.

18
ТЕМА 4. БУЛЕВА АЛГЕБРА: СДНФ
Здесь требуется знать, какие переменные называются логическими,
что такое набор значений переменных, как формулируются теоремы
де Моргана. Необходимо иметь чёткое представление о таких понятиях,
как логические операции дизъюнкции, конъюнкции и инверсии, дизъюнк-
тивные и конъюнктивные нормальные формы, совершенные формы, мин-
термы, значения функции на заданном наборе, табличное и аналитическое
представления булевых функций, карты Вейча.
Центральным вопросом четвёртой главы пособия является представ-
ление булевой функции в виде совершенной дизъюнктивной нормальной
формы (СДНФ). Найти СДНФ можно при помощи теоремы Шеннона
о разложении булевых функций, применяя её ко всем логическим пере-
менным [22, с. 119], либо воспользоваться способом, описанным в п. 4.7
учебного пособия. Однако проще всего применить карту Вейча. Для этого
необходимо на карту нанести заданную функцию, отметив на ней едини-
цами минтермы, из которых состоят конъюнкции заданной функции,
и мысленно совместить её со стандартной картой. Единицы покажут, какие
номера на стандартной карте являются искомыми минтермами исследуе-
мой функции.
Исходная функция в контрольной задаче задана в КНФ. Следова-
тельно, сначала по теореме де Моргана находим ДНФ инверсии, наносим
её на карту Вейча, затем карту инвертируем и результат сопоставляем
со стандартной картой. Проиллюстрируем эти действия на примере.
Пример. Представить в СДНФ булеву функцию
(
)(
)(
) .
f
A C B D B C D C
19
Решение. Выполняем следующие действия:
1) так как функция представлена в КНФ, то сначала её инвертируем
по теореме де Моргана:
;
C
D
C
B
D
B
C
A
f
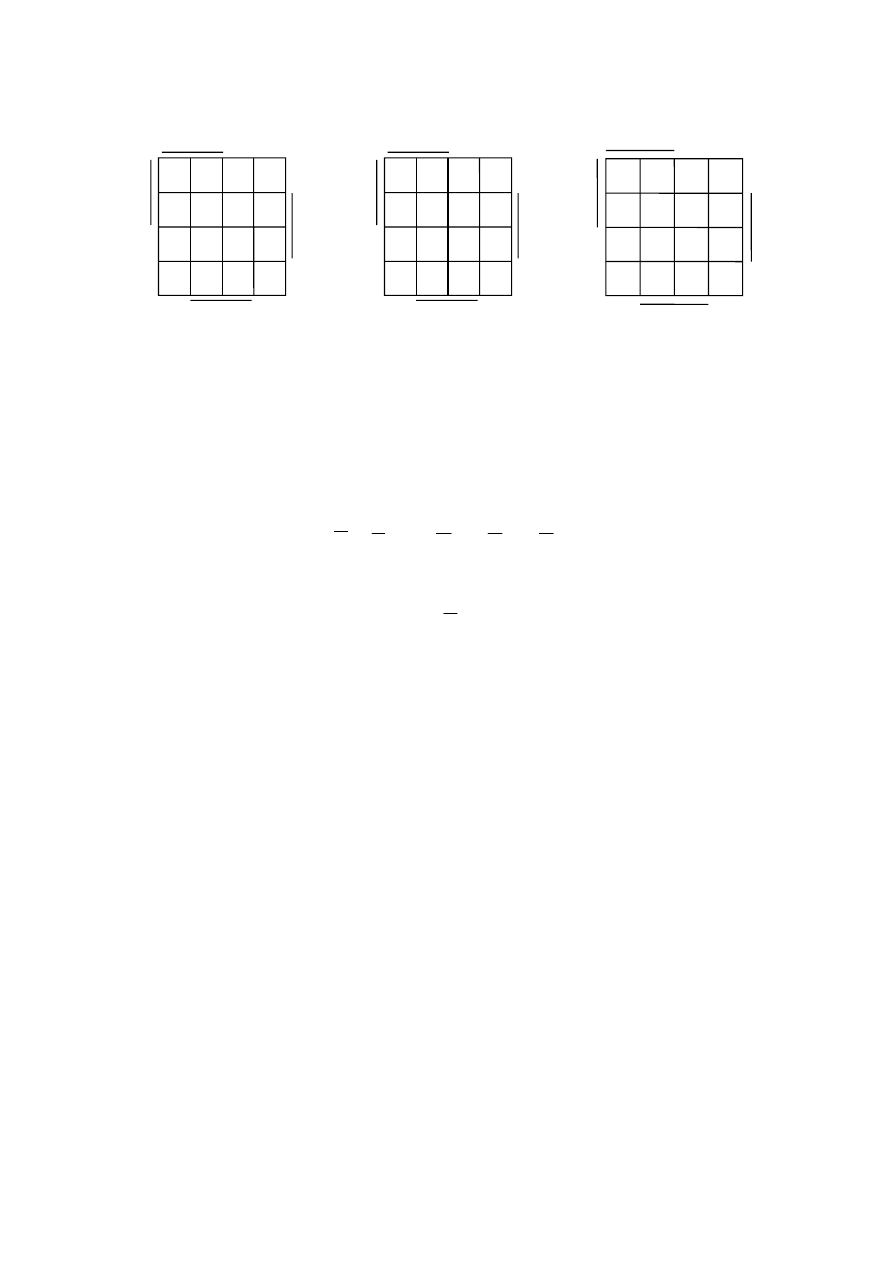
2) наносим инверсию на карту Вейча (рис. 2);
3) инверсию функции f, т. е.
f
, инвертируем. Получим карту для
прямой функции (рис. 3);
4) сопоставляем рис. 3 с рис. 4, где представлена стандартная карта
Вейча, и находим СДНФ заданной функции:
f = (10, 11, 15).
Ответ: 10, 11, 15.
Рис. 2
1
1
1
1
1
1
1
1
D
A
B
C
1
1
1
1
1
Рис. 3
D
A
B
C
1
1
1
Рис. 4
A
B
C
D
12 14 6
4
13 15 7
5
9 11 3
1
8 10 2
0

20
ТЕМА 5. МИНИМИЗАЦИЯ ДИЗЪЮНКТИВНЫХ
НОРМАЛЬНЫХ ФОРМ
Эта тема относится к важнейшим во всей прикладной алгебре логики
темам. Дополнительно к сведениям, приведённым к предыдущей задаче,
для успешной минимизации ДНФ булевых функций необходимо иметь
чёткое представление о содержание таких понятий, как упрощение буле-
вых формул, их минимизация, простая импликанта, операции склеивания
и поглощения (из предыдущей темы), число вхождений переменных, со-
кращённая форма булевой функции, неопределённые состояния.
Для успешного выполнения задания по минимизации ДНФ необхо-
димо научиться отыскивать на карте Вейча простые импликанты, стремясь
к тому, чтобы число импликант было наименьшим и на карте Вейча
не оставалось ни одной свободной единицы, т. е. каждая единица на карте
должна входить хотя бы в одну из простых импликант.
Чтобы освоить карту Вейча, необходимо выполнить ряд упражнений.
Для этого в учебном пособии «Дискретная математика» приведено не-
сколько десятков упражнений на минимизацию с учётом неопределённых
состояний. Здесь же на примере покажем, как необходимо действовать при
решении контрольного задания по минимизации ДНФ.
Пример. Найти минимальную дизъюнктивную нормальную форму
булевой функции, представленной в СДНФ (в квадратных скобках приве-
дены неопределённые состояния):
f = (2, 6, 7, 9, 11, 15), [3, 4, 5, 8, 12].
Определить числа a, b и c, где
a – общее число букв в минимальной ДНФ;
b – число простых импликант, из которых состоит минимальная ДНФ;
c – число знаков дизъюнкции, содержащихся в минимальной ДНФ.