ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.01.2019
Просмотров: 48261
Скачиваний: 391
Ф1.1.2-2
|
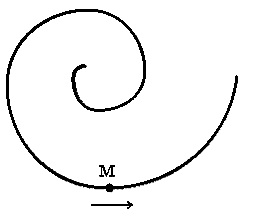
Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …
|
1: уменьшается* 2: увеличивается 3: не изменяется |
|
Нормальное
ускорение
|
|
Ф1.1.2-3
|
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
|
1: уменьшается* 2: увеличивается 3: не изменяется |
|
Нормальное
ускорение
|
|
Ф1.1.2-4
|
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
|
1: увеличивается* 2: уменьшается 3: не изменяется |
|
Нормальное
ускорение
|
|
Ф1.1.2-5
|
Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения …
|
1: уменьшается* 2: увеличивается 3: не изменяется |
|
Полное
ускорение
|
|
Ф1.1.2-6
|
Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости …
|
1: меньше нуля* 2: равна нулю 3: больше нуля |
|
Проекция
тангенциального ускорения на ось
|
|
Ф1.1.2-7
|
Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости …
|
1: больше нуля* 2: меньше нуля 3: равна нулю |
|
|
|
Ф1.1.3-1
|
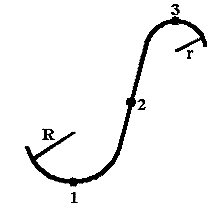
Материальная точка движется с постоянной по величине скоростью вдоль плоской кривой. Ее полное ускорение максимально …
|
1: в т. 3 траектории* 2: в т. 1 траектории 3: в т. 2 траектории |
|
Полное
ускорение
|
|
Ф1.1.3-2
|
Тело движется с постоянным нормальным ускорением по траектории, изображенной на рисунке
При движении в направлении, указанном стрелкой, величина скорости тела … |
1: уменьшается 2: не изменяется 3:увеличивается* |
|
|
|
Ф1.1.3-3
|
Тело движется с постоянной по величине скоростью по дуге окружности, переходящей в прямую, как показано на рисунке.
Величина нормального ускорения тела до точки А … |
1: увеличивается, потом остается постоянной 2: уменьшается, потом увеличивается 3: увеличивается, потом уменьшается до нуля 4: постоянна, потом уменьшается до нуля* |
|
|
|
Ф1.1.4-1
|
Если
|
1. равномерного движения по окружности 2. прямолинейного равноускоренного движения 3. равномерного криволинейного движения 4. прямолинейного равномерного движения* |
|
Поскольку
|
|
Ф1.1.4-2
|
Если
|
1: прямолинейного равноускоренного движения* 2: прямолинейного равномерного движения 3: равномерного движения по окружности 4: равномерного криволинейного движения |
|
Поскольку
|
|
Ф1.1.4-3
|
Если
|
1: равномерного движения по окружности* 2: прямолинейного равноускоренного движения 3: прямолинейного равномерного движения 4: равномерного криволинейного движения |
|
Поскольку
|
|
Ф1.1.5-1
|
Если
|
1:
2:
3:
4:
|
|
Поскольку
движение равномерное, то модуль
скорости
|
|
Ф1.1.5-2
|
Если
|
1:
2:
3:
4:
|
|
Поскольку
движение прямолинейное, то радиус
кривизны траектории ρ=∞: |
|
Ф1.1.6-1
|
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения… |
1: увеличивается* 2: уменьшается 3: не изменяется |
|
Поскольку
точка М движется по окружности, то
радиус кривизны траектории ρ=const.
По определению тангенциальное ускорение
|
|
Ф1.1.6-2
|
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения… |
1: уменьшается* 2: увеличивается 3: не изменяется |
|
Поскольку
точка М движется по окружности, то
радиус кривизны траектории ρ=const.
По определению тангенциальное ускорение
|
|
Ф1.1.7-1
|
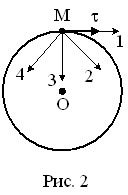
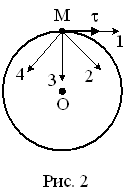
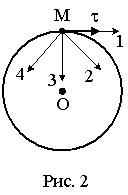
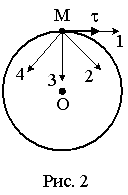
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 3* 2: 1 3: 2 4: 4 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-2
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 4* 2: 1 3: 2 4: 3 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-3
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 3* 2: 1 3: 2 4: 4 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-4
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 4* 2: 1 3: 2 4: 3 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-5
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 2* 2: 1 3: 3 4: 4 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-6
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 2* 2: 1 3: 3 4: 4 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-7
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 4* 2: 1 3: 2 4: 3 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.7-8
|
Материальная
точка М движется по окружности со
скоростью
Рис. 1 Рис. 2 |
1: 3* 2: 1 3: 2 4: 4 |
|
При
естественном способе ускорение точки
|
|
Ф1.1.8-1
|
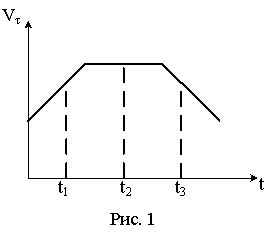
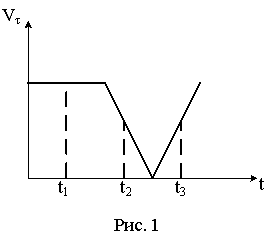
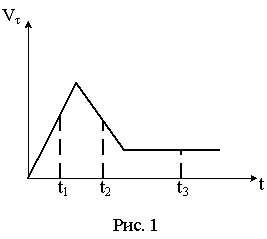
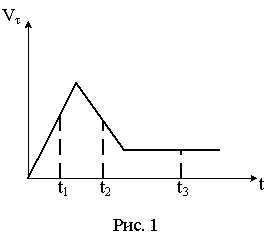
Скорость
автомобиля изменялась во времени, как
показано на графике зависимости
Направление результирующей всех сил, действующих на автомобиль в этот момент времени правильно отображает вектор … |
1. 4* 2. 1 3. 3 4. 2 |
|
Из
графика зависимости
|
|
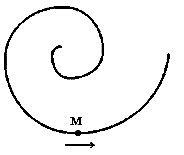
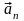 характеризует быстроту изменения
направления скорости:
характеризует быстроту изменения
направления скорости:
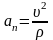 .
Т.к. при движении точки М по спирали
радиус кривизны траектории
.
Т.к. при движении точки М по спирали
радиус кривизны траектории 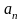 уменьшается.
уменьшается. 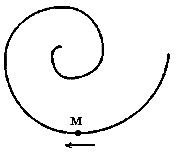
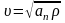
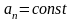 ,
из рисунка видно, что при движении
точки М по спирали радиус кривизны
траектории
,
из рисунка видно, что при движении
точки М по спирали радиус кривизны
траектории 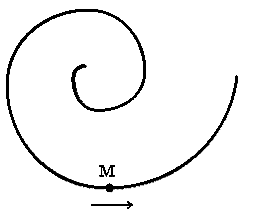
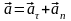 .
Тангенциальное ускорение
.
Тангенциальное ускорение
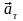 характеризует быстроту изменения
модуля скорости:
характеризует быстроту изменения
модуля скорости:
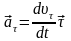 .
Так как по условию модуль скорости
постоянен и
.
Так как по условию модуль скорости
постоянен и
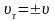 ,
то величина
,
то величина
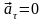 (равномерное движение). Нормальное
ускорение
(равномерное движение). Нормальное
ускорение
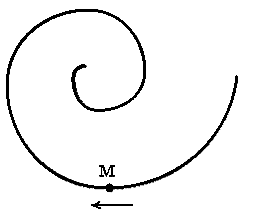
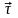
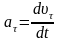
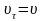
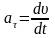 .
.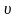 также должна уменьшаться. Следовательно
также должна уменьшаться. Следовательно
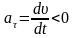
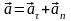 .
По условию
.
По условию
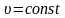
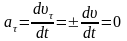 .
Следовательно
.
Следовательно
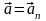 ,
,
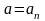 .
По определению
.
По определению
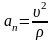 .
.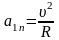
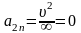
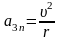
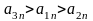
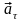 и
и
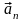 - тангенциальная и нормальная
составляющие ускорения, то соотношения:
- тангенциальная и нормальная
составляющие ускорения, то соотношения:
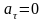 ,
,
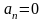 справедливы для …
справедливы для …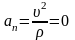 ,
то радиус кривизны траектории ρ=0:
движение прямолинейное. Так как
,
то радиус кривизны траектории ρ=0:
движение прямолинейное. Так как
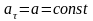 ,
,
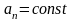 справедливы
для …
справедливы
для …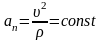 ,
то радиус кривизны траектории ρ=
,
то радиус кривизны траектории ρ=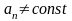
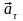 и
и
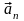 – тангенциальная
и нормальная составляющие ускорения,
то для прямолинейного равноускоренного
движения справедливы соотношения:
– тангенциальная
и нормальная составляющие ускорения,
то для прямолинейного равноускоренного
движения справедливы соотношения: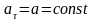 ;
;
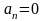 *
*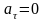 ;
;
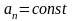
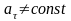 ;
;
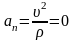 .
Так как движение равноускоренное:
.
Так как движение равноускоренное:
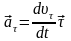 .
Так как проекция тангенциального
ускорения на направление скорости
положительна, то
.
Так как проекция тангенциального
ускорения на направление скорости
положительна, то
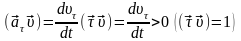 .
Следовательно:
.
Следовательно:
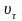 и
и
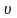 возрастают. Поэтому нормальное
ускорение
возрастают. Поэтому нормальное
ускорение
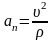 будет увеличиваться.
будет увеличиваться. 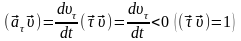 .
Следовательно:
.
Следовательно:
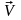
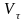 от времени (
от времени (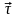 - единичный вектор положительного
направления,
- единичный вектор положительного
направления,
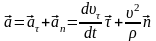 .
В момент времени
.
В момент времени 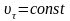 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
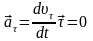 .
Нормальное ускорение
.
Нормальное ускорение
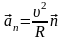
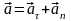 также имеет направление 3.
также имеет направление 3. 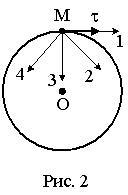
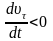 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
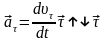
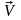
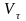 от времени (
от времени (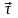 - единичный вектор положительного
направления,
- единичный вектор положительного
направления,
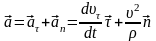 .
В момент времени
.
В момент времени 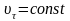 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
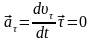 .
Нормальное ускорение
.
Нормальное ускорение
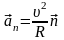
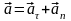 также имеет направление 3.
также имеет направление 3. 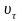
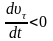 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
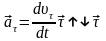
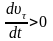 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
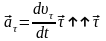
 от времени (
от времени (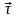 - единичный вектор положительного
направления,
- единичный вектор положительного
направления,
 .
В момент времени
.
В момент времени 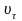
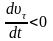 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
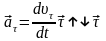
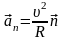
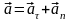 имеет направление 4.
имеет направление 4. 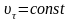 .
При этом тангенциальное ускорение
.
При этом тангенциальное ускорение
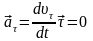 .
Нормальное ускорение
.
Нормальное ускорение
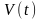 .
В момент времени
.
В момент времени 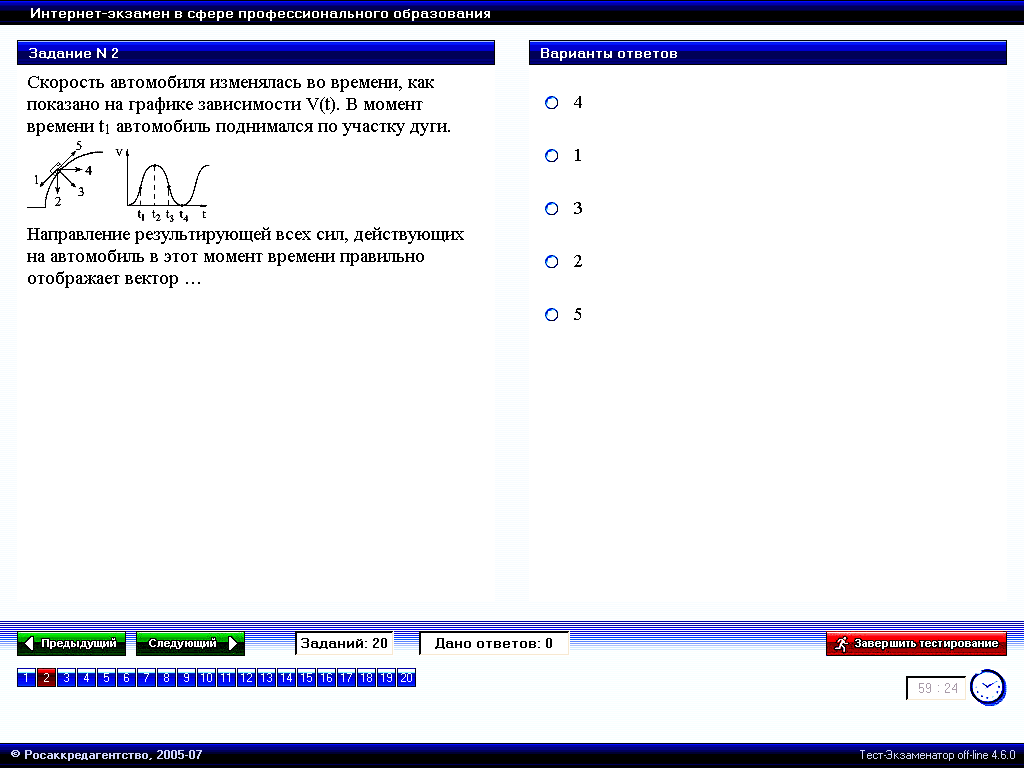
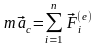 следует,
что направление результирующей всех
сил совпадает с направлением ускорения
центра масс, которое можно разложить
на тангенциальную и нормальную
составляющие:
следует,
что направление результирующей всех
сил совпадает с направлением ускорения
центра масс, которое можно разложить
на тангенциальную и нормальную
составляющие:
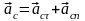 .
Выберем направление единичного вектора
.
Выберем направление единичного вектора
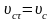 .
К
.
К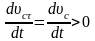
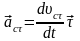 совпадает с направлением 5, указанном
на рисунке. Нормальное ускорение
совпадает с направлением 5, указанном
на рисунке. Нормальное ускорение
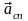 совпадает с направлением 3, указанном
на рисунке. Поэтому направление
ускорения центра масс автомобиля
совпадает с направлением 3, указанном
на рисунке. Поэтому направление
ускорения центра масс автомобиля
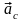 и направление результирующей всех
сил совпадает с направлением 4, указанном
на рисунке.
и направление результирующей всех
сил совпадает с направлением 4, указанном
на рисунке.