Файл: Вариационный анализ на примере группы компаний Токарнофрезерный центр.docx

1. По имеющимся данным объемом n определяют наибольшее х_mах и наименьшее x_min значение контролируемого показателя.

2. Вычисляют размах варьирования значений показателя:

.

.

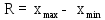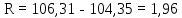3. Определяют число k интервалов группировки при n> 60:

,

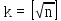Где k – целая часть числа.

k = 9.

4. Устанавливают интервальную длину (ширину) h одинаковую для всех интервалов группировки:

h = R / k.

h = 1,96 / 9 = 0,22.

5. Определяют нижнюю (левую) границу первого интервала группировки:

L₁ = x_min – ∆ / 2;

Где ∆ - наименьший значащий разряд данных.

L₁ = 104,35.

6. Определяют нижние и верхние границы остальных интервалов группировки, используя соотношения:

U₁ = L₁ + h.

U₁ = 104,35 + 0,22 = 104,57.

L_i+1 = U₁.

L₂ = 104,57.

Где I = 1, 2…k.

U₂ = 104,79; L₃ = 104,79; U₃ = 105,00; L₄ = 105,00; U₄ = 105,22; L₅ = 105,22; U₅ = 105,44; L₆ = 105,44; U₆ = 105,66; L₇ = 105,66; U₇ = 105,88; L₈ = 105,88; U₈ = 106,10; L₉ = 106,10; U₉ = 106,32.

Так как x_max 9, то границы рассчитаны верно.

7. Для каждого интервала находят центральное значение (середину интервала):

x_{ц. i} = (U_i + L_i) / 2.

Где L_i и U_i – соответственно нижняя и верхняя границы i-го интервала группировки.

x_{ц. 1} = 104,46; x_{ц. 2} = 104,68; x_{ц. 3} = 104,89; x_{ц. 4} = 105,11; x_{ц. 5} = 105,33; x_{ц. 6} = 105,55; x_{ц. 7} = 105,77; x_{ц. 8} = 105,99; x_{ц. 9} = 106,21.

8. Для каждого интервала группировки подсчитывают абсолютную (m_i) или относительную (m_i/n) частоту (частость) попаданий выборочных значений контролируемой характеристики в этот интервал. Для облегчения подсчета частот воспользовались вспомогательной таблицей (таблица 3).

Таблица 3 – Таблица для подсчета частот при группировке данных

№ п/п	Интервалы			Середина, xц.i		Частота, mi		mi / n
	Li	Ui
1	104,35	104,57	104,46		3		0,03
2	104,57	104,79	104,68		5		0,06
3	104,79	105,00	104,89		10		0,11
4	105,00	105,22	105,11		14		0,16
5	105,22	105,44	105,33		22		0,24
6	105,44	105,66	105,55		12		0,13
7	105,66	105,88	105,77		12		0,13
8	105,88	106,10	105,99		6		0,07
9	106,10	106,32	106,21		6		0,07
Итого					90		1

9. Результаты группировки, как правило, визуализируют в виде столбчатой диаграммы, называемой гистограмма (рисунок 1).


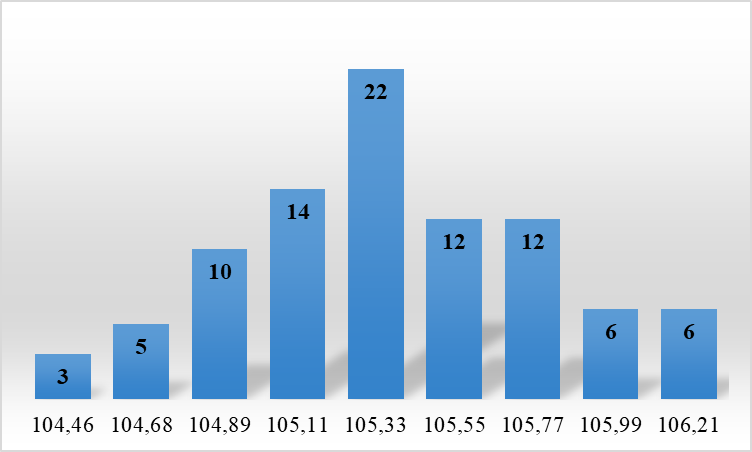
Рисунок 1 – Гистограмма частот
Полигон частот представлен на рисунке 2.



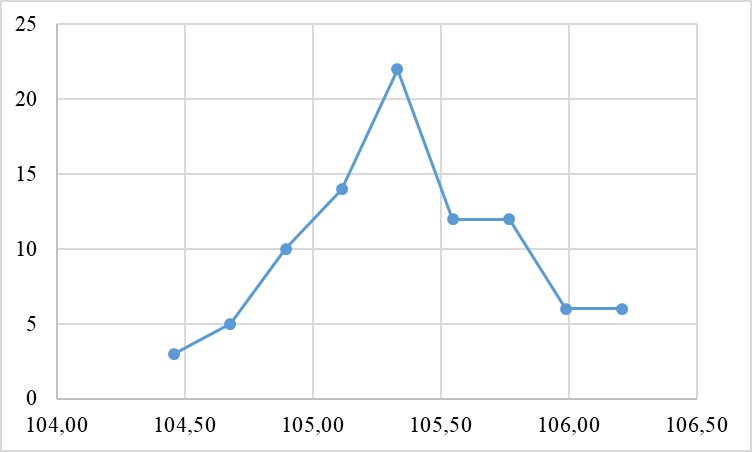
Рисунок 2 – Полигон частот
Гистограмма представляет собой ступенчатую фигуру из столбцов с основаниями равными длине интервалов, и высотами равными частотам (частостям) m_i (m_i/n) для соответствующих интервалов.

Если соединить середины верхних оснований столбцов отрезками прямой, то можно получить полигон частот (для m_i) или полигон относительных частот (для m_i/n).

10. По результатам группировки также строят график эмпирической (выборочной) функции распределения. Эмпирическая функция распределения F_n(х) по сгруппированным данным определяется выражением:

F_n(x) = P [X i] = N_i / n.

Где U_i – верхняя (правая) граница i-го интервала группировки;

N_i – накопленная частота для i-го интервала группировки.

Накопленной частотой i-го интервала группировки называется число Ni наблюдений, численное значение которых меньше или равно правой границе, т.е. удовлетворяющих условию х_j ≤ U_i. Накопленная частота N_i определяется суммированием групповых частот m_i первых i интервалов группировки, т.е. N_i = m₁ + m₂ + … + m_i. В свою очередь, отношения N_i/n представляют собой относительные накопленные частоты.

Для графического представления эмпирической функции распределения строят столбчатую диаграмму, в которой основания столбцов равны ширине интервалов группировки, а высота – относительным накопленным частотам для соответствующего интервала. После этого правые верхние углы столбцов соединяют отрезками прямой линии. Полученная ломаная называется огивой (полигоном накопленных частот) и представляет собой график эмпирической функции распределения для непрерывной случайной величины. График эмпирической (выборочной) функции распределения представлен на рисунке 3.



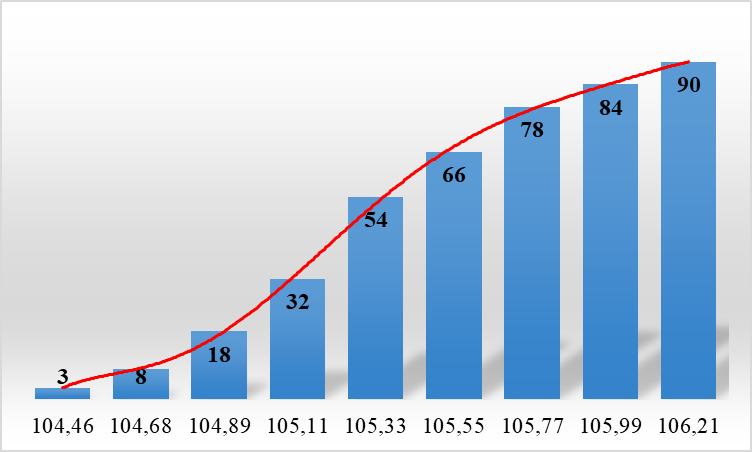
Рисунок 3 – График эмпирической (выборочной) функции распределения

---