ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 67
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- удельная смоченная (активная) поверхность насадки, м2/м3;
при ψ = 1 а = .
.
Применяя объемный коэффициент массопередачи, получаем формулу для высоты единицы переноса:
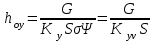 (3.4)
(3.4)
Отсюда при ψ = 1 получаем:
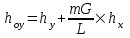
 (3.5)
(3.5)
где G – мольный расход газа , кмоль/с;
L – мольный расход жидкости, кмоль/с;
 - удельная поверхность насадки, м2/м3;
- удельная поверхность насадки, м2/м3;
 - высота единицы переноса для газовой фазы, м ;
- высота единицы переноса для газовой фазы, м ;
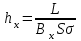 - высота единицы переноса для жидкой фазы, м.
- высота единицы переноса для жидкой фазы, м.
В критериальном уравнении коэффициент массопередачи выражен в кмоль/(м2×с×(кмоль/м3) равен м/с.
Из уравнения
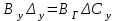 , (3.6)
, (3.6)
находим соотношение и
и 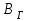 , тогда согласно таблице 6.2 на рисунке 5:
, тогда согласно таблице 6.2 на рисунке 5:
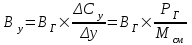 , (3.7)
, (3.7)
Далее:
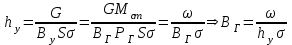 , (3.8)
, (3.8)
где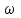 - фиктивная скорость, м/с, находим по формуле:
- фиктивная скорость, м/с, находим по формуле:
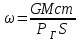 , (3.9)
, (3.9)
В выражение для диффузионного критерия Нуссельта подставим найденное значение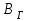 и получим:
и получим:
 , (3.10)
, (3.10)
где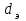 - эквивалентный диаметр, м, найденный по формуле:
- эквивалентный диаметр, м, найденный по формуле:
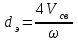 , (3.11)
, (3.11)
где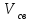 - свободный объем насадки, м3/м3;
- свободный объем насадки, м3/м3;
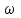 - удельная поверхность насадки, м2/м3.
- удельная поверхность насадки, м2/м3.
Далее получаем:
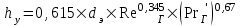
. (3.12)
4.Определить коэффициент массоотдачи для газовой фазы в насадочном абсорбере, в котором производится поглощение диоксида серы из инертного газа (азота) под атмосферным давлением. Температура в абсорбере 220С, он работает в пленочном режиме. Скорость газа в абсорбере (фиктивная) 0,5 м/с. Абсорбер заполнен кусками кокса ( = 50 м2/м3;V=0,72 м3/м3).
= 50 м2/м3;V=0,72 м3/м3).
Решение:
Из критериального уравнения Нуссельта:
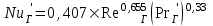 , (4.0)
, (4.0)
где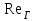 - постоянная Рейнольдса.
- постоянная Рейнольдса.
Рассчитаем постоянную Рейнольдса по формуле:
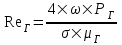 , (4.1)
, (4.1)
где - скорость газа в абсорбере (фиктивная), м/с;
- скорость газа в абсорбере (фиктивная), м/с;
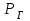 - плотность газа, кг/м3;
- плотность газа, кг/м3;
 - удельная поверхность, м2/м3;
- удельная поверхность, м2/м3;
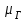 - динамический коэффициент вязкости, Па×с.(0,0175×10-3)
- динамический коэффициент вязкости, Па×с.(0,0175×10-3)
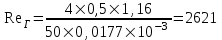
Плотность газа определяем по уравнению:
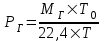 , (4.2)
, (4.2)
где Мг - молярная масса газа (N2),г/моль;
Т0 – абсолютный 00С (2730К);
Т – заданная температура,0С;
22,4 – газовая постоянная (число Авогардо).

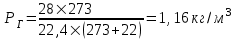 .
.
Коэффициент диффузии принимаем как в воздухе, тогда:
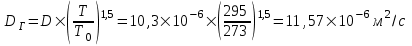 . (4.3)
. (4.3)
Далее:
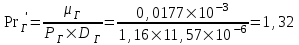
Рассчитаем диффузионный критерий Нуссельта:
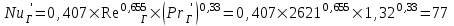 (4.4)
(4.4)
Эквивалентный диаметр рассчитываем по формуле:
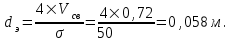 (4.5)
(4.5)
Коэффициент массоотдачи:
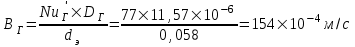 .
.
5.В массообменном аппарате, работающем под давлением
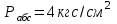 ,коэффициенты массоотдачи имеют следующие значения:
,коэффициенты массоотдачи имеют следующие значения:
 ,
,  .Равновесные составы газовой и жидкой фаз характеризуются законом Генри
.Равновесные составы газовой и жидкой фаз характеризуются законом Генри 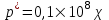 . Определить:
. Определить:
а) коэффициенты массопередачи Ку и Кх;
б) во сколько раз диффузионное сопротивление жидкой фазы отличается от диффузионного сопротивления газовой фазы.
Решение:
Из уравнения идеальной смеси газов доля компонента равняется:
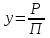 , (5.0)
, (5.0)
где р - парциальное давление компонента газовой смеси;
П – общее давление смеси газов или паров, равное сумме всех парциальных давлений компонентов.
Закон Генри, закон межфазного равновесия для идеальных газов:
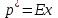 , (5.1)
, (5.1)
где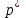 - парциальное давление компонента в газовой фазе над равновесном с газом жидкостью;
- парциальное давление компонента в газовой фазе над равновесном с газом жидкостью;
Е – коэффициент Генри, зависящий от температуры и природы газа и жидкости;
х – мольная доля компонента в жидкости.
Если подставить в уравнение (5.1) значение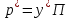 по уравнению (5.0) получим значение:
по уравнению (5.0) получим значение:
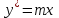 , (5.3)
, (5.3)
где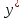 - мольная доля компонента в газовой фазе, равновесной с жидкостью;
- мольная доля компонента в газовой фазе, равновесной с жидкостью;
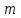 - безразмерный коэффициент, постоянный для системы газ-жидкость при t и П=const равен
- безразмерный коэффициент, постоянный для системы газ-жидкость при t и П=const равен 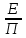 .
.
Уравнение равновесия приведём к виду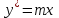 :
:
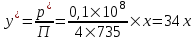 , (5.4)
, (5.4)
Далее найдём коэффициенты массопередачи по формулам:
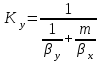 (5.5)
(5.5)
и
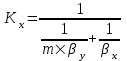 , (5.6)
, (5.6)
где
и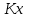 - коэффициенты массопередачи, кмоль/(м2×с);
- коэффициенты массопередачи, кмоль/(м2×с);
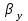 и
и 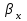 - коэффициенты массоотдачи, кмоль/(м2×с);
- коэффициенты массоотдачи, кмоль/(м2×с);
 - тангенс угла наклона линии равновесия.
- тангенс угла наклона линии равновесия.
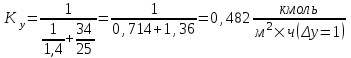 ,
,
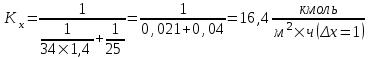 .
.
Проверим равенство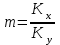 :
:
 . (5.7)
. (5.7)
При движущих силах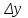 и
и  отношение диффузионных сопротивлений жидкой и газовой фаз будет:
отношение диффузионных сопротивлений жидкой и газовой фаз будет:
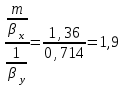 (раз). (5.8)
(раз). (5.8)
6. Воздух атмосферного давления при температуре 400С насыщен водяным паром. Определить парциальное давление воздуха, объемный и массовый % пара в воздушно-паровой смеси и его относительную массовую концентрацию, считая оба компонента смеси идеальными газами. Атмосферное давление 750 мм рт. ст. Определить также плотность воздушно – паровой смеси, сравнить её с плотностью сухого воздуха.
Решение:
Давление насыщенного пара при температуре 400С составляет 55,32 мм рт.ст. Это будет парциальное давление водяного пара в воздушно – паровой смеси, а парциальное давление воздуха будет:
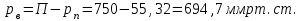 , (6.0)
, (6.0)
где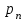 - парциальное давление водяного пара, мм рт. ст.;
- парциальное давление водяного пара, мм рт. ст.;
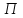 - атмосферное давление, мм рт.ст.
- атмосферное давление, мм рт.ст.
Вычислим долю водяного пара в смеси (объемную):
 . (6.1)
. (6.1)
Вычислим массовую долю пара:
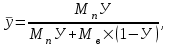 (6.2)
(6.2)
где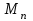 - молярная масса пара, г/моль.
- молярная масса пара, г/моль.
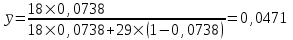 .
.
Вычислим относительную массовую концентрацию:
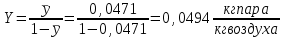
. (6.3)
Плотность воздушно-паровой смеси рассчитываем исходя из суммы плотностей всех компонентов, при своем парциальном давлении по формуле:
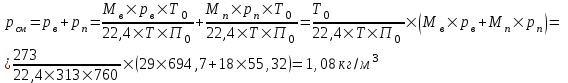 (6.4)
(6.4)
Плотность смеси при заданных температуре и давлении рассчитаем по формуле:
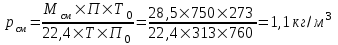 , (6.5)
, (6.5)
Плотность сухого воздуха при заданных температуре и давлении:
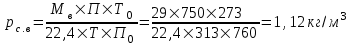 .
.
7.Жидкая смесь содержит 65% (мол.) толуола и 35% (мол.) четыреххлористого углерода (ч.х.у.). Определить относительную массовую концентрацию толуола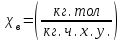 и его объемную массовую концентрацию
и его объемную массовую концентрацию 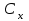 (в кг/м3).
(в кг/м3).
Решение:
Относительную массу толуола рассчитаем по формуле:
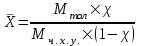 , (7.1)
, (7.1)
где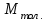 - мольная масса толуола (92 кг/моль);
- мольная масса толуола (92 кг/моль);
 - мольная масса четыреххлористого углерода (154 кг/моль);
- мольная масса четыреххлористого углерода (154 кг/моль);
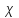 - мольная доля толуола.
- мольная доля толуола.
Тогда:
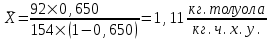 .
.
Для расчёта объемной массовой концентрации толуола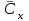 , необходимо вычислить плотность смеси
, необходимо вычислить плотность смеси 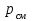 , для этого сначала найдем массовую долю толуола по формуле:
, для этого сначала найдем массовую долю толуола по формуле:
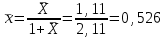 . (7.2)
. (7.2)
Плотность толуола, исходя из данных рисунка 1, составляет 870 кг/м3, плотность четыреххлористого углерода составляет 1630 кг/м3.
Изменение объема при смешении не происходит, значит, объем смеси равен объему сумме компонентов, тогда объем кг смеси составит:
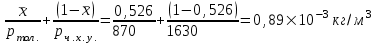 , (7.3)
, (7.3)
тогда плотность смеси:
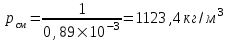 . (7.4)
. (7.4)
 Объемная массовая концентрация толуола рассчитывается по формуле:
Объемная массовая концентрация толуола рассчитывается по формуле:
при ψ = 1 а =
 .
.Применяя объемный коэффициент массопередачи, получаем формулу для высоты единицы переноса:
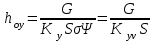 (3.4)
(3.4)Отсюда при ψ = 1 получаем:
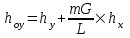
 (3.5)
(3.5)где G – мольный расход газа , кмоль/с;
L – мольный расход жидкости, кмоль/с;
 - удельная поверхность насадки, м2/м3;
- удельная поверхность насадки, м2/м3; - высота единицы переноса для газовой фазы, м ;
- высота единицы переноса для газовой фазы, м ;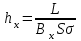 - высота единицы переноса для жидкой фазы, м.
- высота единицы переноса для жидкой фазы, м.В критериальном уравнении коэффициент массопередачи выражен в кмоль/(м2×с×(кмоль/м3) равен м/с.
Из уравнения
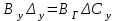 , (3.6)
, (3.6)находим соотношение
 и
и 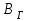 , тогда согласно таблице 6.2 на рисунке 5:
, тогда согласно таблице 6.2 на рисунке 5: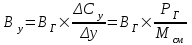 , (3.7)
, (3.7)Далее:
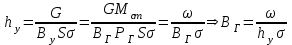 , (3.8)
, (3.8)где
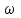 - фиктивная скорость, м/с, находим по формуле:
- фиктивная скорость, м/с, находим по формуле: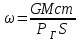 , (3.9)
, (3.9)В выражение для диффузионного критерия Нуссельта подставим найденное значение
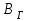 и получим:
и получим: , (3.10)
, (3.10)где
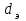 - эквивалентный диаметр, м, найденный по формуле:
- эквивалентный диаметр, м, найденный по формуле: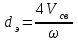 , (3.11)
, (3.11)где
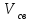 - свободный объем насадки, м3/м3;
- свободный объем насадки, м3/м3;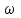 - удельная поверхность насадки, м2/м3.
- удельная поверхность насадки, м2/м3.Далее получаем:
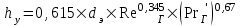
. (3.12)
4.Определить коэффициент массоотдачи для газовой фазы в насадочном абсорбере, в котором производится поглощение диоксида серы из инертного газа (азота) под атмосферным давлением. Температура в абсорбере 220С, он работает в пленочном режиме. Скорость газа в абсорбере (фиктивная) 0,5 м/с. Абсорбер заполнен кусками кокса (
 = 50 м2/м3;V=0,72 м3/м3).
= 50 м2/м3;V=0,72 м3/м3).Решение:
Из критериального уравнения Нуссельта:
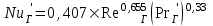 , (4.0)
, (4.0)где
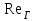 - постоянная Рейнольдса.
- постоянная Рейнольдса.Рассчитаем постоянную Рейнольдса по формуле:
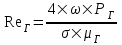 , (4.1)
, (4.1)где
 - скорость газа в абсорбере (фиктивная), м/с;
- скорость газа в абсорбере (фиктивная), м/с;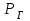 - плотность газа, кг/м3;
- плотность газа, кг/м3; - удельная поверхность, м2/м3;
- удельная поверхность, м2/м3;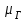 - динамический коэффициент вязкости, Па×с.(0,0175×10-3)
- динамический коэффициент вязкости, Па×с.(0,0175×10-3)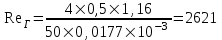
Плотность газа определяем по уравнению:
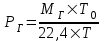 , (4.2)
, (4.2)где Мг - молярная масса газа (N2),г/моль;
Т0 – абсолютный 00С (2730К);
Т – заданная температура,0С;
22,4 – газовая постоянная (число Авогардо).

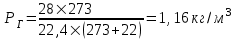 .
.Коэффициент диффузии принимаем как в воздухе, тогда:
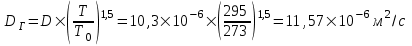 . (4.3)
. (4.3)Далее:
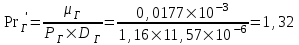
Рассчитаем диффузионный критерий Нуссельта:
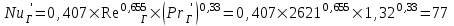 (4.4)
(4.4)Эквивалентный диаметр рассчитываем по формуле:
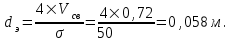 (4.5)
(4.5)Коэффициент массоотдачи:
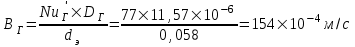 .
.5.В массообменном аппарате, работающем под давлением
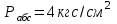 ,коэффициенты массоотдачи имеют следующие значения:
,коэффициенты массоотдачи имеют следующие значения: ,
,  .Равновесные составы газовой и жидкой фаз характеризуются законом Генри
.Равновесные составы газовой и жидкой фаз характеризуются законом Генри 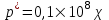 . Определить:
. Определить:а) коэффициенты массопередачи Ку и Кх;
б) во сколько раз диффузионное сопротивление жидкой фазы отличается от диффузионного сопротивления газовой фазы.
Решение:
Из уравнения идеальной смеси газов доля компонента равняется:
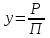 , (5.0)
, (5.0)где р - парциальное давление компонента газовой смеси;
П – общее давление смеси газов или паров, равное сумме всех парциальных давлений компонентов.
Закон Генри, закон межфазного равновесия для идеальных газов:
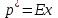 , (5.1)
, (5.1)где
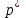 - парциальное давление компонента в газовой фазе над равновесном с газом жидкостью;
- парциальное давление компонента в газовой фазе над равновесном с газом жидкостью;Е – коэффициент Генри, зависящий от температуры и природы газа и жидкости;
х – мольная доля компонента в жидкости.
Если подставить в уравнение (5.1) значение
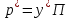 по уравнению (5.0) получим значение:
по уравнению (5.0) получим значение: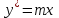 , (5.3)
, (5.3)где
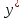 - мольная доля компонента в газовой фазе, равновесной с жидкостью;
- мольная доля компонента в газовой фазе, равновесной с жидкостью;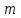 - безразмерный коэффициент, постоянный для системы газ-жидкость при t и П=const равен
- безразмерный коэффициент, постоянный для системы газ-жидкость при t и П=const равен 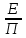 .
.Уравнение равновесия приведём к виду
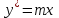 :
: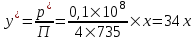 , (5.4)
, (5.4)Далее найдём коэффициенты массопередачи по формулам:
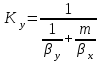 (5.5)
(5.5)и
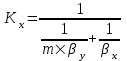 , (5.6)
, (5.6)где

и
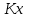 - коэффициенты массопередачи, кмоль/(м2×с);
- коэффициенты массопередачи, кмоль/(м2×с);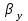 и
и 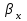 - коэффициенты массоотдачи, кмоль/(м2×с);
- коэффициенты массоотдачи, кмоль/(м2×с); - тангенс угла наклона линии равновесия.
- тангенс угла наклона линии равновесия.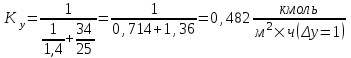 ,
,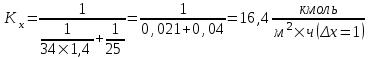 .
.Проверим равенство
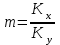 :
: . (5.7)
. (5.7)При движущих силах
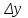 и
и  отношение диффузионных сопротивлений жидкой и газовой фаз будет:
отношение диффузионных сопротивлений жидкой и газовой фаз будет: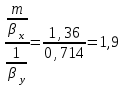 (раз). (5.8)
(раз). (5.8)6. Воздух атмосферного давления при температуре 400С насыщен водяным паром. Определить парциальное давление воздуха, объемный и массовый % пара в воздушно-паровой смеси и его относительную массовую концентрацию, считая оба компонента смеси идеальными газами. Атмосферное давление 750 мм рт. ст. Определить также плотность воздушно – паровой смеси, сравнить её с плотностью сухого воздуха.
Решение:
Давление насыщенного пара при температуре 400С составляет 55,32 мм рт.ст. Это будет парциальное давление водяного пара в воздушно – паровой смеси, а парциальное давление воздуха будет:
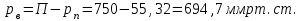 , (6.0)
, (6.0)где
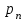 - парциальное давление водяного пара, мм рт. ст.;
- парциальное давление водяного пара, мм рт. ст.;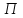 - атмосферное давление, мм рт.ст.
- атмосферное давление, мм рт.ст.Вычислим долю водяного пара в смеси (объемную):
 . (6.1)
. (6.1)Вычислим массовую долю пара:
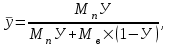 (6.2)
(6.2)где
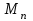 - молярная масса пара, г/моль.
- молярная масса пара, г/моль.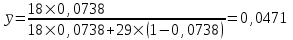 .
.Вычислим относительную массовую концентрацию:
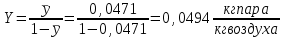
. (6.3)
Плотность воздушно-паровой смеси рассчитываем исходя из суммы плотностей всех компонентов, при своем парциальном давлении по формуле:
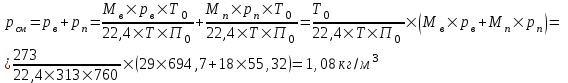 (6.4)
(6.4)Плотность смеси при заданных температуре и давлении рассчитаем по формуле:
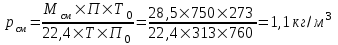 , (6.5)
, (6.5)Плотность сухого воздуха при заданных температуре и давлении:
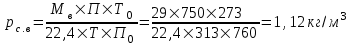 .
.7.Жидкая смесь содержит 65% (мол.) толуола и 35% (мол.) четыреххлористого углерода (ч.х.у.). Определить относительную массовую концентрацию толуола
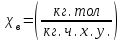 и его объемную массовую концентрацию
и его объемную массовую концентрацию 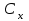 (в кг/м3).
(в кг/м3).Решение:
Относительную массу толуола рассчитаем по формуле:
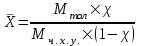 , (7.1)
, (7.1)где
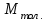 - мольная масса толуола (92 кг/моль);
- мольная масса толуола (92 кг/моль); - мольная масса четыреххлористого углерода (154 кг/моль);
- мольная масса четыреххлористого углерода (154 кг/моль);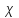 - мольная доля толуола.
- мольная доля толуола.Тогда:
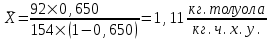 .
.
Для расчёта объемной массовой концентрации толуола
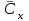 , необходимо вычислить плотность смеси
, необходимо вычислить плотность смеси 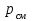 , для этого сначала найдем массовую долю толуола по формуле:
, для этого сначала найдем массовую долю толуола по формуле: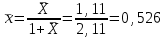 . (7.2)
. (7.2)Плотность толуола, исходя из данных рисунка 1, составляет 870 кг/м3, плотность четыреххлористого углерода составляет 1630 кг/м3.
Изменение объема при смешении не происходит, значит, объем смеси равен объему сумме компонентов, тогда объем кг смеси составит:
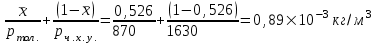 , (7.3)
, (7.3)тогда плотность смеси:
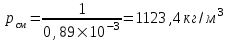 . (7.4)
. (7.4) Объемная массовая концентрация толуола рассчитывается по формуле:
Объемная массовая концентрация толуола рассчитывается по формуле: