ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Бөгеткеқарсы кодтау Мысал ретінде Х0-Х7 (6.1a-сурет) үшразрядты кодтық сөздердің толық жиынтығын қарастырайық.
 ұндағы кез келген қателік жіберілген Хi сөзін қате тануға әкеледі. Егер кодтық комбинациялар жиынтығымен шектелсек, онда жіберу кезіндегі бір қателік қажетсіз сөзді қабылдауға әкеледі және оны тауып алуға болады. Бұл шығын бағасымен жүзеге асады (мысалы, төрт символды кодтау үшін екі разряд таб жеткілікті) – 6.1 б-сурет. Егер разрядтың максималды санымен ерекшеленетін екі сөзбен ғана шектелсек, онда екіретті қатені табуға болады, ал біреуін түзетуге де болады (6.1в-сурет). Екі кодтық сөз арасындағы сәйкес келмейтін разрядтар санын d-ны кодтық арақашықтық деп атайық (100 мен 010 сөздері үшін d = 2, ал 010 мен 011кодтық сөздер үшін d = 1мәні). Кодтық сөздердің толық жинағы минималды кодтық арақашықтықпен dmin сипатталады. Шығынсыз код үшін (6.1 а-сурет) dmin = 1, 6.1б-суреттегі код үшін dmin = 2, 6.1в – суреттегі код үшін dmin = 3. Минималды кодтық арақашықтық қателікті табу мен түзету мүмкіндігін анықтайды. 6.2-суретте келесі қатынасты сипаттайды.
 (6.2)
 (6.3)(6.1) – (6.3) қа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
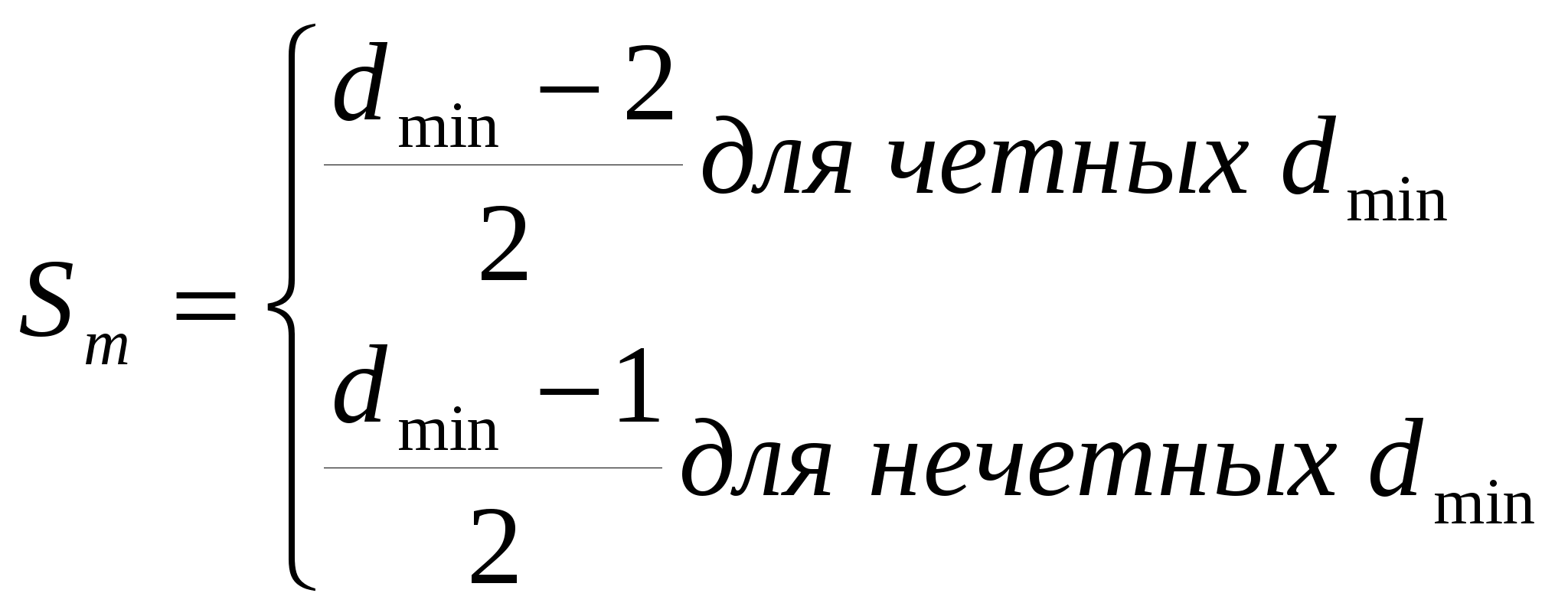) қателіктер ортасында дербес бөлінген. l >> dmin ұзындығымен қатені табатын кодтар бар.Нақтылыққа тексеретін код
Бұл код өзінің жеңілдігімен кең таралды. Мұндай кодтаудың мысалы жоғарыда қарастырылды. Жалпы түрде оны былайша сипаттауға болады:
-
кодтау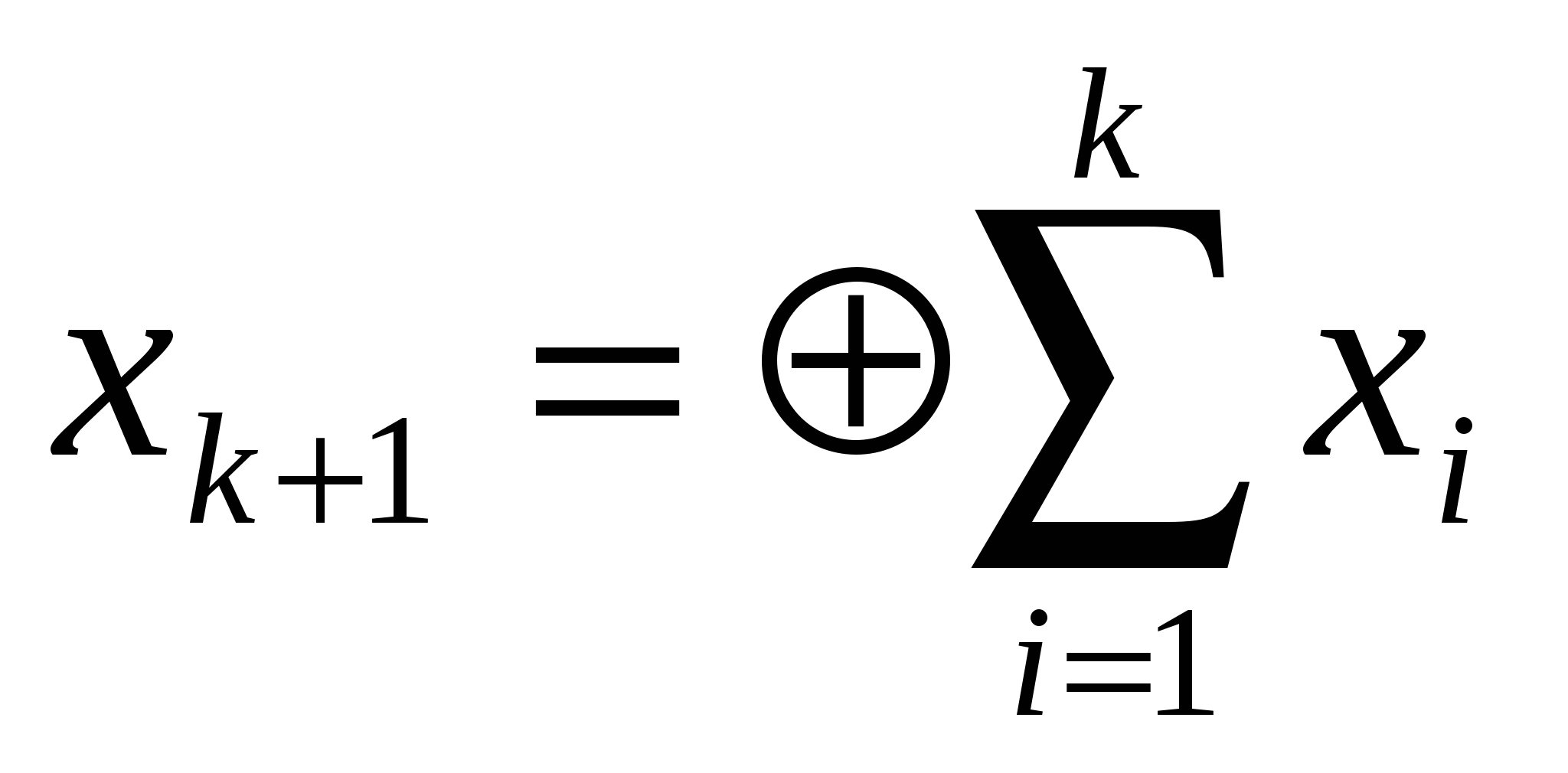
(6.4) операциясына келтіріледі, к+1 номерімен бақылаушы бит k ақпараттық разрядты нақтылыққа дейін толықтырады;
-
декодтау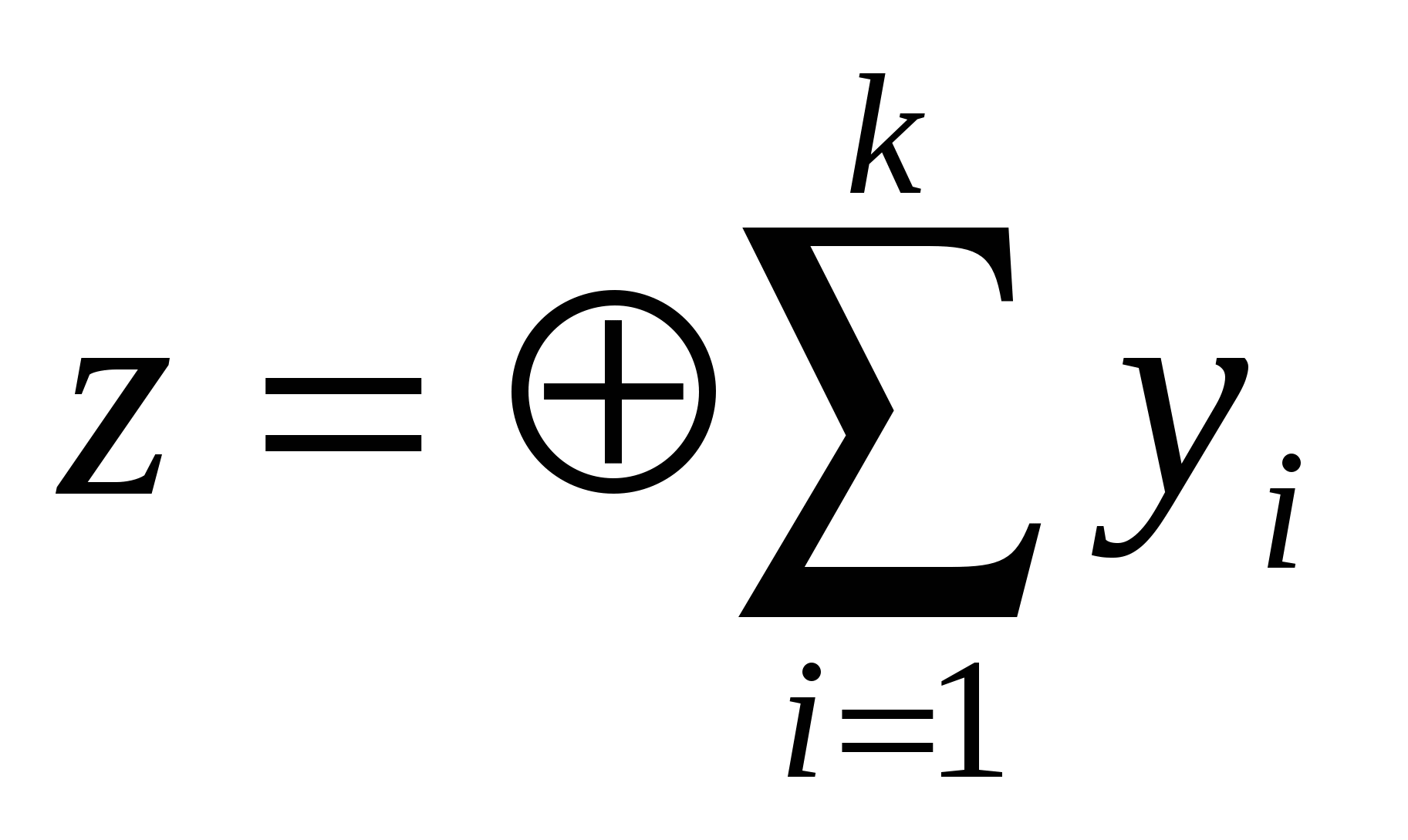
(6.5) есептеу жолымен орындалады, егер Z=0 (реттілік сақталған), берілу қатесіз өтті, Z=1 берілу қате болғанын айтады.
Мұндай кодқа dmin =2, r=1.
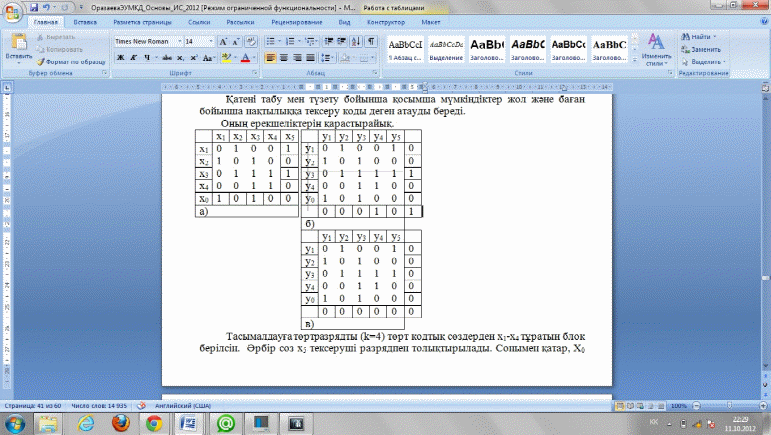
Қатені табу мен түзету бойынша қосымша мүмкіндіктер жол және баған бойынша нақтылыққа тексеру коды деген атауды береді.
Оның ерекшеліктерін қарастырайық.
| Бөгеткеқарсы кодтау Мысал ретінде Х0-Х7 (6.1a-сурет) үшразрядты кодтық сөздердің толық жиынтығын қарастырайық.
 ұндағы кез келген қателік жіберілген Хi сөзін қате тануға әкеледі. Егер кодтық комбинациялар жиынтығымен шектелсек, онда жіберу кезіндегі бір қателік қажетсіз сөзді қабылдауға әкеледі және оны тауып алуға болады. Бұл шығын бағасымен жүзеге асады (мысалы, төрт символды кодтау үшін екі разряд таб жеткілікті) – 6.1 б-сурет. Егер разрядтың максималды санымен ерекшеленетін екі сөзбен ғана шектелсек, онда екіретті қатені табуға болады, ал біреуін түзетуге де болады (6.1в-сурет). Екі кодтық сөз арасындағы сәйкес келмейтін разрядтар санын d-ны кодтық арақашықтық деп атайық (100 мен 010 сөздері үшін d = 2, ал 010 мен 011кодтық сөздер үшін d = 1мәні). Кодтық сөздердің толық жинағы минималды кодтық арақашықтықпен dmin сипатталады. Шығынсыз код үшін (6.1 а-сурет) dmin = 1, 6.1б-суреттегі код үшін dmin = 2, 6.1в – суреттегі код үшін dmin = 3. Минималды кодтық арақашықтық қателікті табу мен түзету мүмкіндігін анықтайды. 6.2-суретте келесі қатынасты сипаттайды.
 (6.2)
 (6.3)(6.1) – (6.3) қатынастары dmin анықтамасына сәйкес ең жаман жағдайға есептелген. Нақты жағдайларда қатені тауып, оны түзетуге болады. Дәріс №14. Өзін-өзі тексеру сұрақтары немесе тесттер
Дәріс №15. АҚПАРАТТЫҚ ҮРДІСТЕР – АҚПАРАТТЫҚ ЖҮЙЕЛЕРІНІҢ НЕГІЗДЕРІ. АРНАЛЫҚ ДЕҢГЕЙДЕГІ АҚПАРАТТЫҚ ҮРДІС
Аналогты-кодтық түрлендіргіштер Бөгетке қарсы кодтарға қатысты жалпы ескертулер жасайық. Біріншіден, кодтың маңызды сипаттамасы қателікке қарсы тұра алатын оның мүмкіндігі болып табылады. l ұзындықты қателікті xi – xi + l көрші разрядтар жинағы түсіндіреді, мұнда xi мен xi + l разрядтар қате, ал аралық xj (  ) қателіктер ортасында дербес бөлінген. l >> dmin ұзындығымен қатені табатын кодтар бар.Екіншіден, кодтық сөздің ұзындығы үлкен болған сайын, соншалықты аз бөлігін берілген деңгейді dmin қамтамасыз ететін шығынды разрядтар құрайды. Яғни шығынды кодтау ұзын сөздер үшін орындау тиімді. Үшіншіден, шығынды разрядтар сөздің барлық ұзындығы бойынша бөлінуі мүмкін. Бұл жағдайда кодтық сөз келесі құрылымға ие:
Кодтау процедурасы k ақпараттық бойынша хj шығынды m разрядты алуды білдіреді. Нақтылыққа тексеретін код Бұл код өзінің жеңілдігімен кең таралды. Мұндай кодтаудың мысалы жоғарыда қарастырылды. Жалпы түрде оны былайша сипаттауға болады:
Мұндай кодқа dmin =2, r=1. Қатені табу мен түзету бойынша қосымша мүмкіндіктер жол және баған бойынша нақтылыққа тексеру коды деген атауды береді. Оның ерекшеліктерін қарастырайық. 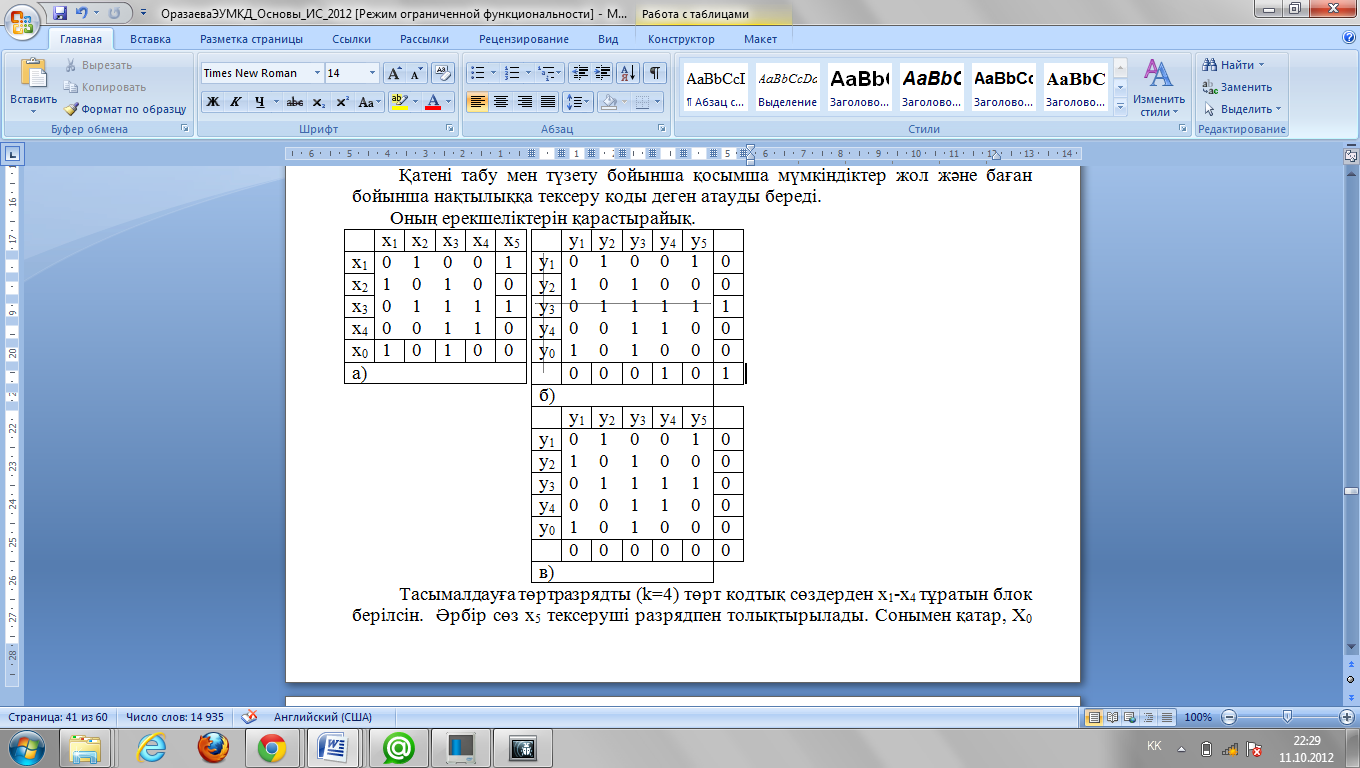 Тасымалдауға төртразрядты (k=4) төрт кодтық сөздерден х1-х4 тұратын блок берілсін. Әрбір сөз х5 тексеруші разрядпен толықтырылады. Сонымен қатар, X0 тексеруші кодтық сөз қосымша құрылады, оның барлық разрядтары блоктағы берілетін сөздердің сәйкесінше биттерінің қосындысынан алынады:  Бір қате болған кезде Yj кодтық сөздің алынған блогын тексеру үшінші сөздің төртінші қатарында қателік кеткенін көрсетеді. Координаттар нүктесімен көрсету кеткен қателікті түзетуге мүмкіндік береді. Мұндай кодтың минималды кодтық арақашықтығы жол мен баған бойынша кодтық арақашықтықтың көбейтіндісіне тең: dmin=2х2=4, демек, кодпен табылатын қателіктің максималды реттілігі r=4-1=3. Шындығында да, r=4 үшін қателік табылмайтын жағдай бар | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||