2) применение дополнительных устройств, таких как компенсаторы износа, фильтры, протекторы для защиты от пыли, съемники быстро изнашивающихся деталей, предохранители и др.;

3) улучшение характеристик материалов за счет применения высокопрочных материалов, антифрикционных материалов, упрочненных накладок, проката переменного сечения и др.;

4) улучшение смазки, в том числе обеспечение жидкостного трения, герметизация узлов трения, применение гидродинамической и аэрозольной смазки, автоматизация смазки и др.



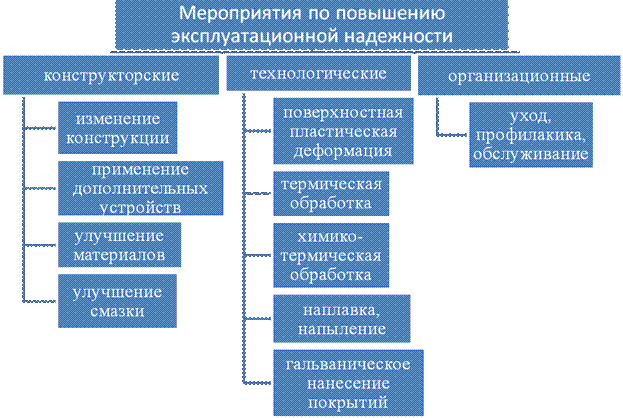
Рисунок 12 - Классификация мероприятий по повышению эксплуатационной надежности технологического оборудования

Технологические мероприятия по повышению надежности можно условно разделить на следующие группы:

1) поверхностная пластическая деформация (наклеп), основными видами которой являются дробеструйная обработка, обкатка шариками и роликами, термомеханическая обработка, электромеханическое сглаживание и др.;

2) термическая обработка, в том числе поверхностная газовая закалка, закалка в электролите, закалка токами высокой частоты, упрочнение взрывом, цементация и др.;

3) химико-термическая обработка – азотирование, хромирование, цианирование, алитирование, никелирование и др.;

4) наплавка и напыление, к которым относятся газовая, электродуговая и электрошлаковая наплавка, газовая металлизация, плазменное напыление и др.;

5) гальваническое нанесение покрытий – цинкование, хромирование, никелирование, борирование, эмалирование, фосфатирование и др.

Организационные мероприятия по повышению надежности включают работы по уходу, профилактике, обслуживанию и ремонту: контроль состояния и режимов работы оборудования, планово-предупредительный ремонт, уход за поверхностями трения, обслуживание смазочных систем, повышение квалификации и ответственности рабочих и др.

2.3. Оценка надежности методами теории вероятности и математической статистики

Надежность объектов нарушается возникающими отказами. Отказы рассматривают как случайные события. Для количественной оценки надежности используются методы теории вероятности и математической статистики. Показатели надежности могут определяться чисто аналитическим путем на основе математической модели – математического определения надежности. Показатели надежности могут определяться в результате обработки опытных данных – это статистическое определение показателя надежности.

---

Момент возникновения отказа, частота возникновения отказов – величины случайные. Поэтому базовыми методами для теории надежности являются методы теории вероятности и математической статистики. Случайное событие – событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Случайное событие характеризуется вероятностью реализации Р.

Случайная величина – величина, которая в результате опыта принимает одно, наперед неизвестное значение, зависящее от случайных причин. Случайные величины могут быть дискретными и непрерывными.

Все возможные на практике значения некоторой случайной величины образуют генеральную совокупность случайной величины.

Ряд конкретных реализаций случайной величины называют выборочной совокупностью или выборкой.

Генеральная совокупность характеризуется статистическими параметрами: математическое ожидание – среднее значение случайной величины ; дисперсия D – мера рассеивания случайной величины относительно среднего значения:

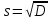(19)

где s – среднее квадратическое (стандартное) отклонение случайной величины.

На практике математическое ожидание и дисперсию случайной величины можно оценить только на основе выборки из конечного числа наблюдений (измерений) случайной величины:

– выборочное среднее арифметическое значение случайной величины

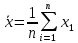(20)

где n – число наблюдений, xi – реализация случайной величины в каждом наблюдении.

– исправленное выборочное среднее квадратическое отклонение случайной величины (выборочное стандартное отклонение)

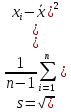(21)

где s – выборочное среднее квадратическое (стандартное) отклонение случайной величины, являющееся оценкой стандартного отклонения генеральной совокупности.

Кроме среднего арифметического для оценки математического ожидания могут использоваться медиана и мода, а для оценки дисперсии – размах.

Случайная величина характеризуется законом распределения, который связывает значения случайной величины с вероятностью их появления. Для характеристики закона распределения случайной величины используются следующие функции.

Функция распределения случайной величины – функция F(х), определяющая вероятность того, что случайная величина Х в результате испытаний примет значение меньше или равное х:

---

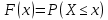(22)


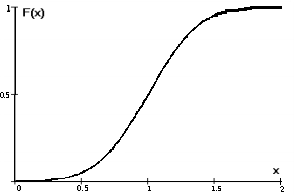
Рисунок 13 - Функция распределения случайной величины

Плотность распределения вероятностей случайной величины

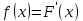(23)

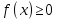(24)

Плотность вероятности характеризует вероятность того, что случайная величина примет конкретное значение x (рис. 14). Плотность вероятности и функция распределения связаны зависимостью.


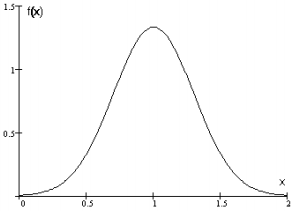
Рисунок 14 - Плотность вероятности.
Показатели надежности могут рассчитываться на основе функции распределения и плотности распределения (математическое определение), а также на основе статистических данных эксплуатации и испытаний (статистическое определение).

Экспериментальной оценкой плотности вероятности случайной величины является гистограмма распределения случайной величины (рис. 15).


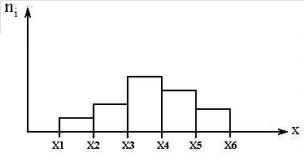
Рисунок 15 - Гистограмма распределения случайной величины

Гистограмма показывает зависимость количества наблюдаемых значений случайной величины в определенном интервале значений от границ этих интервалов. По гистограмме можно приближенно судить о плотности распределения случайной величины.

При построении гистограммы в выборке случайной величины x из n значений определяют наибольшее 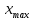и наименьшее 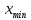значения. Диапазон изменения величины

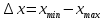(25)

разбивают на m одинаковых интервалов. Затем подсчитывают число наблюдаемых значений случайной величины ni , попадающих в каждый i-тый интервал.

2.4. Расчет оптимального натяжения ткани

Цель процесса промывки: удаление загрязнений из текстильного материала в моющий раствор (водный или органический).

При промывке ткани (рис. 16) целесообразно аналитически определить следующие технологические параметры:

• 
  скорость промывки;
  
• 
  напряжение и деформация ткани;
  
• 
  уровень воды в процессе промывки;
  
• 
  уровень давления воды, пара и воздуха в процессе;
  
• 
  натяжение ткани в процессе промывки.
  

---

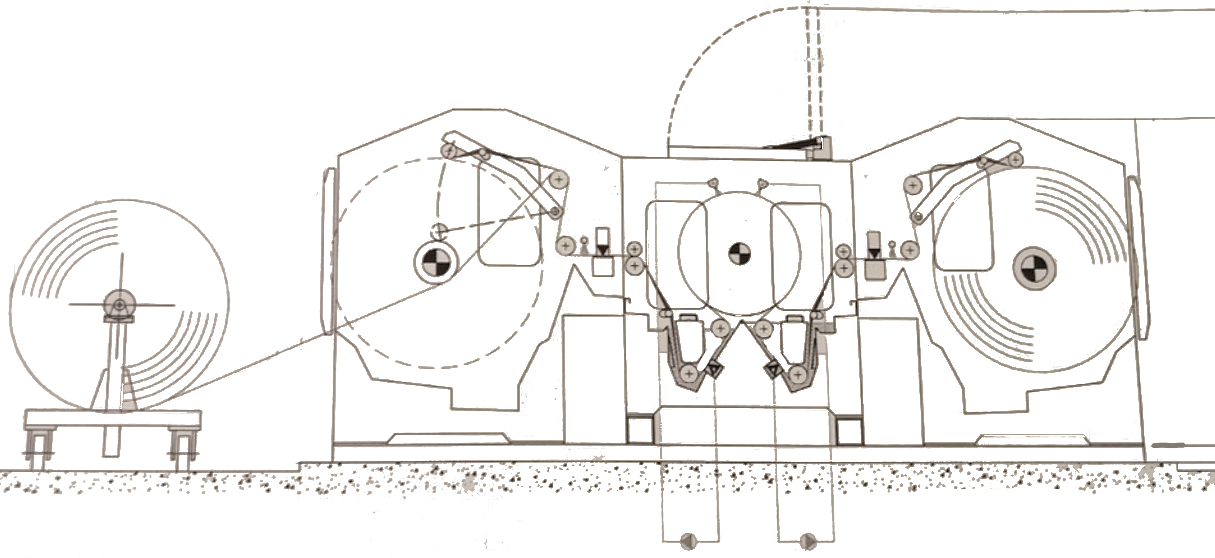
Рисунок 16 – Схема процесса промывки ткани машины периодической промывки модели «HYDRA»

Натяжение ткани должно быть одинаковым и по возможности равномерным по ширине полотна. Неправильное и неравномерное натяжение ткани приводит к снижению качества промывки.

Натяжение ткани должно быть оптимальным, чтобы обеспечить наивысшую производительность труда и оборудования, высокое качество промывки.

Значительное увеличение натяжения ткани ухудшает качество промывки ткани, т.к. происходит значительная вытяжка, вследствие этого, ткань имеет большую усадку по ширине и длине после стирки.

Таким образом, натяжение ткани должно быть оптимальным, чтобы обеспечить максимальную производительность и высокое качество промывки с минимальными затратами.

Рассчитаем оптимальное натяжение ткани на промывочной машине марки «HYDRA» методами математической статистики.

Технические данные машины периодической промывки:

1) Тип ткани – Хлопок – ПЭС;

2) Ширина ткани – 1 800 мм;

3) Ширина валов – 2000 мм;

4) Общая длинна машины – 6 610 мм;

5) Общая ширина машины – 3 214 мм;

6) Общая высота машины – 3 300 мм;

7) Диаметр цилиндров намотки – 320 мм;

8) Диаметр намотки ткани на цилиндре – 1 550 мм;

9) Минимальная скорость – 10 м/мин;

10) Максимальная скорость – 140 м/мин;

11) Натяжение ткани – от 50 до 500 Н;

12) Давление воды – 2-3 Бар;

13) Давление пара – 3 Бар;

14) Давление воздуха – 7 Бар;

15) Мощность электрожвигателя – 53 кВт.

Натяжение ткани при промывке колеблется в пределах 50-500 Н.

Определим оптимальное количество групп с равными интервалами по формуле Стреджесса:

n=1+3,322lg 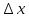(27)

где 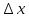– диапазон изменения величины, формула (25)

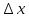=500-50=450 Н

Рассчитаем значения:

n=1+3,322lg450=9,81. Принимаем 10.

Определим величину интервала:

i=(Х_max-X_min)/n (28)

i=(500-50)/10=45

Получаем группировку данных:

50; 50+45=95; 140; 185; 230; 275; 320; 365; 410; 455; 500.

Получаем закрытый интервал, поэтому n принимаем равным 11.

---

По формуле (20) найдем выборочное среднее арифметическое значение случайной величины:



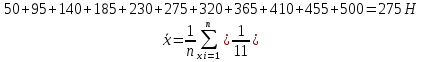
По формуле (21) найдем выборочное среднее квадратическое отклонение случайной величины (выборочное стандартное отклонение):

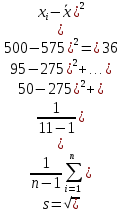Н

По формуле (19) найдем дисперсию:

D=s²= 36²= 1296

Дисперсия показывает средний квадрат отклонений каждой величины от среднего значения.

Далее определим коэффициент вариации по формуле:

V= 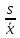100% =  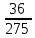100% = 13% (29)

Коэффициент вариации используется для характеристики однородности системы и адекватности расчетов.

Система считается однородной, а расчеты адекватными, если коэффициент вариации не превышает 33 %.

Таким образом, система однородна, расчеты адекватны, а оптимальное натяжение ткани равно 275 Н.

Натяжение ткани при промывке необходимо поддерживать на данном уровне, чтобы обеспечить максимальную производительность труда и оборудования и высокое качество промывки.

---

Смотрите также файлы

• 1 Предмет бизнесстатистика как науки. Статистика.doc

• Студенты это будущее каждой страны. Это молодые граждане нашего общества, полные неиссякаемой энергии и инновациооных идей, фантастических планов и благородных амбиций, надежд и мечтаний.doc

• Отчет по лабораторной работе 5 по дисциплине Информатика.docx

• Томский государственный университет систем управления и радиоэлектроники образовательный.pdf

• Страховые случаи в системе добровольного страхования.pdf