Файл: Лабораторная работа 3 по дисциплине Программные средства для анализа и синтеза систем управления Создание объектов типа lti.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 | Министерство науки и высшего образования РФ федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» (ФГБОУ ВО «СамГТУ») |
Кафедра
«Автоматика и управление в технических системах»
Лабораторная работа №3
по дисциплине
«Программные средства для анализа и синтеза систем управления»
Создание объектов типа LTI-system в Control System Toolbox (CST) Преобразование оъектов
Вариант 4
Выполнил: студенты гр. 2-ИТФ-4
Лощёнин Н.А.
Артюх М.В.
Принял:
профессор Рогачев Г.Н.
Самара 2023
Задание 1
Система sys1 имеет 2 входа и 4 выхода, sys2 - 3 входа и 2 выхода, sys3- 4 входа и 2 выхода.
Таблица 1
| sys1
sys2
sys3
|
1.1 Создать системы в zpk-форме по заданным значениям полюсов и нулей (таблица 1).
1.1 Выполнение
poles = {[-3+ 4i -3- 4i] [-2+ 4i -2- 4i];
[-2+ 4i -2- 4i] [-5+ 2i -5- 2i];
[-4+ 2i -4- 2i] [-4+ 5i -4- 5i];
[-3+ 3i -3- 3i] [-3+ 2i -3- 2i]};
zeros = {-11 -11; -10 -11; -10 -18; -7 -17};
gain = [2 3; 2 6; 2 3; 3 2];
>> sys1 = zpk(poles, zeros, gain)
sys1 =
From input 1 to output...
2 (s^2 + 6s + 25)
1: -----------------
(s+11)
2 (s^2 + 4s + 20)
2: -----------------
(s+10)
2 (s^2 + 8s + 20)
3: -----------------
(s+10)
3 (s^2 + 6s + 18)
4: -----------------
(s+7)
From input 2 to output...
3 (s^2 + 4s + 20)
1: -----------------
(s+11)
6 (s^2 + 10s + 29)
2: ------------------
(s+11)
3 (s^2 + 8s + 41)
3: -----------------
(s+18)
2 (s^2 + 6s + 13)
4: -----------------
(s+17)
Continuous-time zero/pole/gain model.
1.2 Выполнить с помощью команды series последовательное соединение sys1 и sys2, при котором выходы 1 и 3 системы sys1 соединяются с входами 2 и 3 системы sys2. Записать, какие входной и выходной векторы будет иметь результирующая система. Перечислить полюса и нули результирующей системы.
1.2 Выполнение
>> z2={-20 -10 -6; -22 -2 -9}
z2 =
2×3 cell array
{[-20]} {[-10]} {[-6]}
{[-22]} {[ -2]} {[-9]}
>> p2={[-3+2i -3-2i] [-3+3i -3-3i] [-1+1i -1-1i]; [-1+3i -1-3i] [-4+4i -4-4i] [-1+2i -1-2i]
}
p2 =
2×3 cell array
{1×2 double} {1×2 double} {1×2 double}
{1×2 double} {1×2 double} {1×2 double}
>> k2=[5 6 3;1 5 4]
k2 =
5 6 3
1 5 4
>> sys2=zpk(z2,p2,k2)
sys2 =
From input 1 to output...
5 (s+20)
1: ---------------
(s^2 + 6s + 13)
(s+22)
2: ---------------
(s^2 + 2s + 10)
From input 2 to output...
6 (s+10)
1: ---------------
(s^2 + 6s + 18)
5 (s+2)
2: ---------------
(s^2 + 8s + 32)
From input 3 to output...
3 (s+6)
1: --------------
(s^2 + 2s + 2)
4 (s+9)
2: --------------
(s^2 + 2s + 5)
Continuous-time zero/pole/gain model.
>> outs1=[2 3];
>> inputs2=[1 3];
>> sys23=series(sys1,sys2,[2 3],[1 3])
sys23 =
From input 1 to output...
16 (s+14.36) (s+10) (s^2 + 2.422s + 3.695)
(s^2 + 7.966s + 20.44)
1: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 8s + 20)
(s^2 + 4s + 20)
10 (s+10.43) (s+10) (s^2 + 1.767s + 7.421)
(s^2 + 6.204s + 24.29)
2: -----------------------------------------------
(s^2 + 2s + 5) (s^2 + 8s + 20) (s^2 + 2s + 10)
(s^2 + 4s + 20)
From input 2 to output...
39 (s+19.53) (s+10.63) (s^2 + 2.421s + 2.812)
(s^2 + 8.196s + 39.9)
1: ------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 10s + 29)
(s^2 + 8s + 41)
18 (s+19.32) (s+10.19) (s^2 + 2.303s + 7.859)
(s^2 + 8.52s + 30.93)
2: ------------------------------------------------
(s^2 + 2s + 5) (s^2 + 10s + 29) (s^2 + 2s + 10)
(s^2 + 8s + 41)
Continuous-time zero/pole/gain model.
1.3 Выполнить с помощью команды parallel параллельное соединение sys2 и sys3, при котором первые два входа системы sys2 соединяются с последними двумя входами системы sys3, а вторые выходы систем объединяются. Записать, какие входной и выходной векторы будет иметь результирующая система. Перечислить полюса и нули результирующей системы.
1.3 Выполнеие
>> z3={-11 -16 -20 -15; -17 -20 -7 -4}
z3 =
2×4 cell array
{[-11]} {[-16]} {[-20]} {[-15]}
{[-17]} {[-20]} {[ -7]} {[ -4]}
k3 =
6 4 1 1
5 3 4 1
>> p3={[-1 -4] [-6 -4] [-5 -2] [-5 -3];[-5 -3] [-4 -5] [-4 -2] [-1 -2]}
p3 =
2×4 cell array
{[-1 -4]} {[-6 -4]} {[-5 -2]} {[-5 -3]}
{[-5 -3]} {[-4 -5]} {[-4 -2]} {[-1 -2]}
>> sys3 = zpk(z3,p3,k3)
sys3 =
From input 1 to output...
6 (s+11)
1: -----------
(s+1) (s+4)
5 (s+17)
2: -----------
(s+5) (s+3)
From input 2 to output...
4 (s+16)
1: -----------
(s+6) (s+4)
3 (s+20)
2: -----------
(s+4) (s+5)
From input 3 to output...
(s+20)
1: -----------
(s+5) (s+2)
4 (s+7)
2: -----------
(s+4) (s+2)
From input 4 to output...
(s+15)
1: -----------
(s+5) (s+3)
(s+4)
2: -----------
(s+1) (s+2)
Continuous-time zero/pole/gain model.
>> parallel3=parallel(sys2,sys3, [1 2], [3 4],[2],[2])
parallel3 =
From input 1 to output...
3 (s+6)
1: --------------
(s^2 + 2s + 2)
4 (s+9)
2: --------------
(s^2 + 2s + 5)
From input 2 to output...
6 (s+20) (s+4.5) (s+2.333)
1: ---------------------------
(s+5) (s+2) (s^2 + 6s + 13)
5 (s+8.515) (s^2 + 4.285s + 10.71)
2: ----------------------------------
(s+4) (s+2) (s^2 + 2s + 10)
From input 3 to output...
7 (s+11.01) (s^2 + 7.418s + 15.18)
1: ----------------------------------
(s+5) (s+3) (s^2 + 6s + 18)
6 (s+3.15) (s^2 + 3.017s + 7.831)
2: ---------------------------------
(s+2) (s+1) (s^2 + 8s + 32)
From input 4 to output...
6 (s+11)
1: -----------
(s+1) (s+4)
5 (s+17)
2: -----------
(s+5) (s+3)
From input 5 to output...
4 (s+16)
1: -----------
(s+6) (s+4)
3 (s+20)
2: -----------
(s+4) (s+5)
Continuous-time zero/pole/gain model.
1.4 Выполнить задание 1.2 с помощью команд append и connect. Входной и выходной векторы результирующих систем должны быть такими же, как в предыдущих заданиях. Сравнить передаточные функции систем.
1.4 Выполнение
>> app4=append(sys1,sys2)
app4 =
From input 1 to output...
2 (s+11)
1: ---------------
(s^2 + 6s + 25)
2 (s+10)
2: ---------------
(s^2 + 4s + 20)
2 (s+10)
3: ---------------
(s^2 + 8s + 20)
3 (s+7)
4: ---------------
(s^2 + 6s + 18)
5: 0
6: 0
From input 2 to output...
3 (s+11)
1: ---------------
(s^2 + 4s + 20)
6 (s+11)
2: ----------------
(s^2 + 10s + 29)
3 (s+18)
3: ---------------
(s^2 + 8s + 41)
2 (s+17)
4: ---------------
(s^2 + 6s + 13)
5: 0
6: 0
From input 3 to output...
1: 0
2: 0
3: 0
4: 0
5 (s+20)
5: ---------------
(s^2 + 6s + 13)
(s+22)
6: ---------------
(s^2 + 2s + 10)
From input 4 to output...
1: 0
2: 0
3: 0
4: 0
6 (s+10)
5: ---------------
(s^2 + 6s + 18)
5 (s+2)
6: ---------------
(s^2 + 8s + 32)
From input 5 to output...
1: 0
2: 0
3: 0
4: 0
3 (s+6)
5: --------------
(s^2 + 2s + 2)
4 (s+9)
6: --------------
(s^2 + 2s + 5)
qc41=connect(app4,[3 2;5 3], [1 2], [5 6])
qc41 =
A =
x1 x2 x3 x4 x5 x6
x1 -2 4 0 0 0 0
x2 -4 -2 0 0 0 0
x3 0 0 -4 2 0 0
x4 0 0 -2 -4 0 0
x5 0 0 0 0 -5 2
x6 0 0 0 0 -2 -5
x7 0 0 0 0 0 0
x8 0 0 0 0 0 0
x9 0 0 0 0 0 0
x10 7.826 3.913 0 0 29.61 9.871
x11 0 0 0 0 0 0
x12 3.557 1.778 0 0 13.46 4.486
x13 0 0 0 0 0 0
x14 0 0 7.619 2.54 0 0
x15 0 0 0 0 0 0
x16 0 0 6.851 2.284 0 0
x7 x8 x9 x10 x11 x12
x1 0 0 0 0 0 0
x2 0 0 0 0 0 0
x3 0 0 0 0 0 0
x4 0 0 0 0 0 0
x5 0 0 0 0 0 0
x6 0 0 0 0 0 0
x7 -4 5 0 0 0 0
x8 -5 -4 0 0 0 0
x9 0 0 -3 2 0 0
x10 0 0 -2 -3 0 0
x11 0 0 0 0 -1 3
x12 0 0 0 0 -3 -1
x13 0 0 0 0 0 0
x14 11 3.929 0 0 0 0
x15 0 0 0 0 0 0
x16 9.892 3.533 0 0 0 0
x13 x14 x15 x16
x1 0 0 0 0
x2 0 0 0 0
x3 0 0 0 0
x4 0 0 0 0
x5 0 0 0 0
x6 0 0 0 0
x7 0 0 0 0
x8 0 0 0 0
x9 0 0 0 0
x10 0 0 0 0
x11 0 0 0 0
x12 0 0 0 0
x13 -1 1 0 0
x14 -1 -1 0 0
x15 0 0 -1 2
x16 0 0 -2 -1
B =
u1 u2
x1 0 0
x2 2.991 0
x3 0 0
x4 3.557 0
x5 0 0
x6 0 3.557
x7 0 0
x8 0 3.449
x9 0 0
x10 0 0
x11 0 0
x12 0 0
x13 0 0
x14 0 0
x15 0 0
x16 0 0
C =
x1 x2 x3 x4 x5 x6
y1 0 0 0 0 0 0
y2 0 0 0 0 0 0
x7 x8 x9 x10 x11 x12
y1 0 0 7.264 0.8546 0 0
y2 0 0 0 0 2.632 0.3761
x13 x14 x15 x16
y1 3.321 0.6643 0 0
y2 0 0 3.94 0.985
D =
u1 u2
y1 0 0
y2 0 0
Continuous-time state-space model.
>> bode(sys23,qc41)
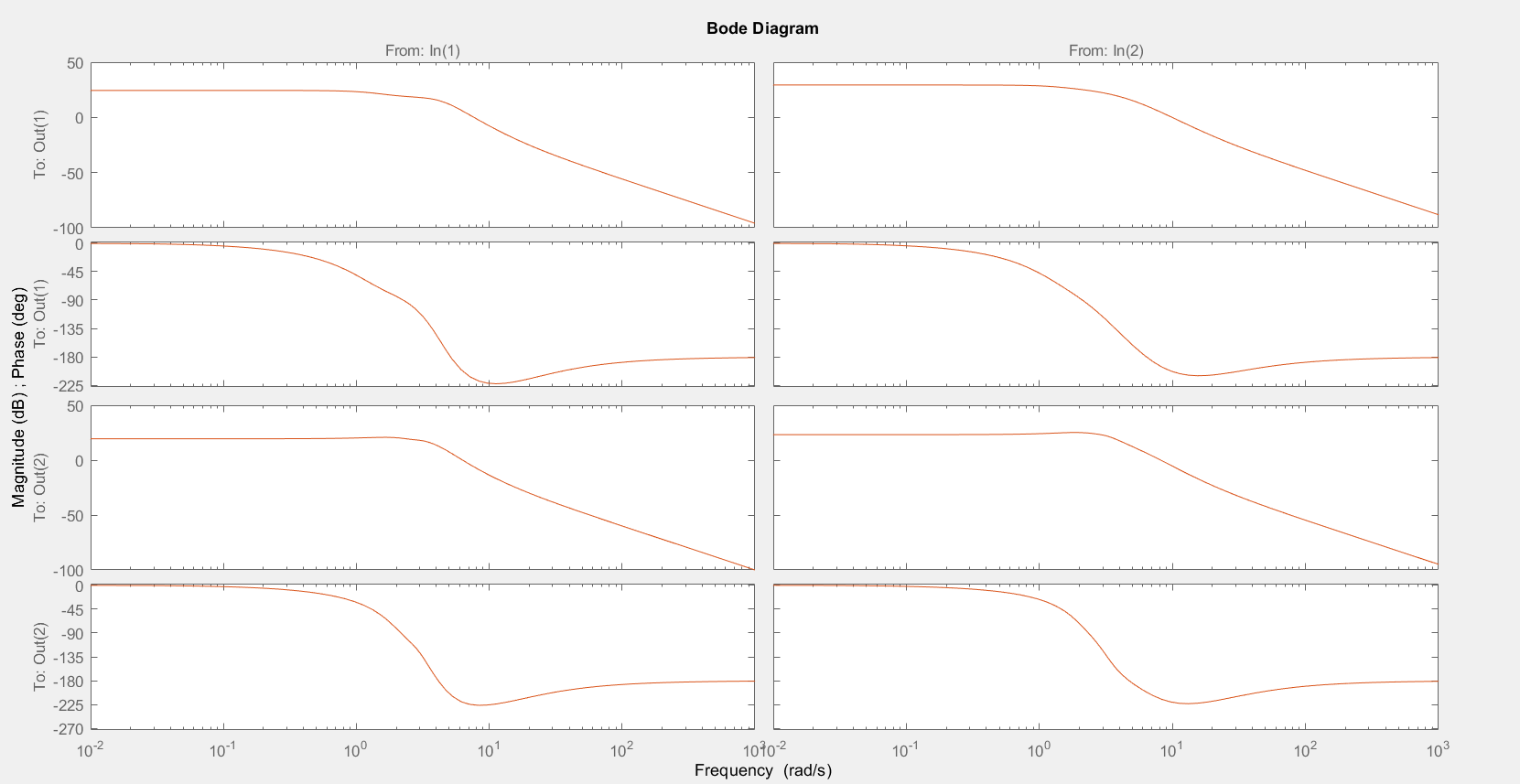
1.5 Выполнить задание 1.3 с помощью команд append и connect. Входной и выходной векторы результирующих систем должны быть такими же, как в предыдущих заданиях. Сравнить передаточные функции систем.
1.5 Выполнение
>> sys5 = tf([1]);
>> sys6 = tf([1]);
>> sys7 = tf([1]);
app51= append(sys2, sys3, sys5, sys6, sys7)
app51 =
From input 1 to output...
5 (s+20)
1: ---------------
(s^2 + 6s + 13)
(s+22)
2: ---------------
(s^2 + 2s + 10)
3: 0
4: 0
5: 0
6: 0
7: 0
From input 2 to output...
6 (s+10)
1: ---------------
(s^2 + 6s + 18)
5 (s+2)
2: ---------------
(s^2 + 8s + 32)
3: 0
4: 0
5: 0
6: 0
7: 0
From input 3 to output...
3 (s+6)
1: --------------
(s^2 + 2s + 2)
4 (s+9)
2: --------------
(s^2 + 2s + 5)
3: 0
4: 0
5: 0
6: 0
7: 0
From input 4 to output...
1: 0
2: 0
6 (s+11)
3: -----------
(s+1) (s+4)
5 (s+17)
4: -----------
(s+5) (s+3)
5: 0
6: 0
7: 0
From input 5 to output...
1: 0
2: 0
4 (s+16)
3: -----------
(s+6) (s+4)
3 (s+20)
4: -----------
(s+4) (s+5)
5: 0
6: 0
7: 0
From input 6 to output...
1: 0
2: 0
(s+20)
3: -----------
(s+5) (s+2)
4 (s+7)
4: -----------
(s+4) (s+2)
5: 0
6: 0
7: 0
From input 7 to output...
1: 0
2: 0
(s+15)
3: -----------
(s+5) (s+3)
(s+4)
4: -----------
(s+1) (s+2)
5: 0
6: 0
7: 0
From input 8 to output...
1: 0
2: 0
3: 0
4: 0
5: 1
6: 0
7: 0
From input 9 to output...
1: 0
2: 0
3: 0
4: 0
5: 0
6: 1
7: 0
From input 10 to output...
1: 0
2: 0
3: 0
4: 0
5: 0
6: 0
7: 1
>> app52=connect(app51,[1 5; 6 5; 2 6; 7 6; 10 2; 10 4],[3 6 7 4 5], [1 2 3]);
>> bode(parallel3,app52)
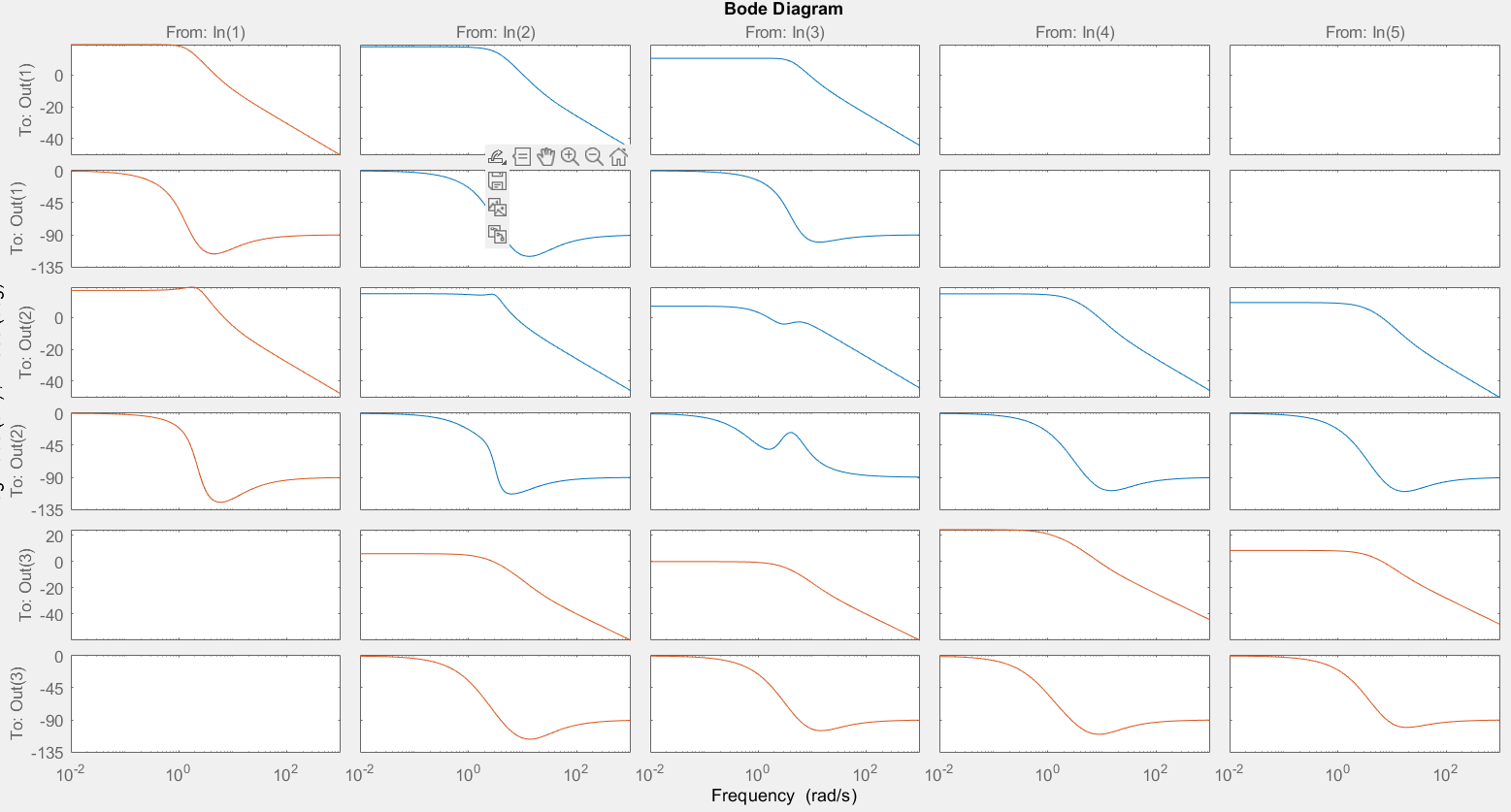
2 Преобразовать полученные в пп. 1.4 и 1.5 системы в ss-форму.
2 Выполнение
Пункт 1.5
SS5 = ss(app51)
SS5 =
A =
x1 x2 x3 x4 x5 x6 x7 x8
x1 -3 2 0 0 0 0 0 0
x2 -2 -3 0 0 0 0 0 0
x3 0 0 -1 3 0 0 0 0
x4 0 0 -3 -1 0 0 0 0
x5 0 0 0 0 -3 3 0 0
x6 0 0 0 0 -3 -3 0 0
x7 0 0 0 0 0 0 -4 4
x8 0 0 0 0 0 0 -4 -4
x9 0 0 0 0 0 0 0 0
x10 0 0 0 0 0 0 0 0
x11 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0
x17 0 0 0 0 0 0 0 0
x18 0 0 0 0 0 0 0 0
x19 0 0 0 0 0 0 0 0
x20 0 0 0 0 0 0 0 0
x21 0 0 0 0 0 0 0 0
x22 0 0 0 0 0 0 0 0
x23 0 0 0 0 0 0 0 0
x24 0 0 0 0 0 0 0 0
x25 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 0 0
x27 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 0 0
x9 x10 x11 x12 x13 x14 x15 x16
x1 0 0 0 0 0 0 0 0
x2 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0
x9 -1 1 0 0 0 0 0 0
x10 -1 -1 0 0 0 0 0 0
x11 0 0 -1 2 0 0 0 0
x12 0 0 -2 -1 0 0 0 0
x13 0 0 0 0 -1 3.162 0 0
x14 0 0 0 0 0 -4 0 0
x15 0 0 0 0 0 0 -3 3.742
x16 0 0 0 0 0 0 0 -5
x17 0 0 0 0 0 0 0 0
x18 0 0 0 0 0 0 0 0
x19 0 0 0 0 0 0 0 0
x20 0 0 0 0 0 0 0 0
x21 0 0 0 0 0 0 0 0
x22 0 0 0 0 0 0 0 0
x23 0 0 0 0 0 0 0 0
x24 0 0 0 0 0 0 0 0
x25 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 0 0
x27 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 0 0
x17 x18 x19 x20 x21 x22 x23 x24
x1 0 0 0 0 0 0 0 0
x2 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0
x9 0 0 0 0 0 0 0 0
x10 0 0 0 0 0 0 0 0
x11 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0
x17 -4 3.464 0 0 0 0 0 0
x18 0 -6 0 0 0 0 0 0
x19 0 0 -4 4 0 0 0 0
x20 0 0 0 -5 0 0 0 0
x21 0 0 0 0 -2 4.243 0 0
x22 0 0 0 0 0 -5 0 0
x23 0 0 0 0 0 0 -2 2.236
x24 0 0 0 0 0 0 0 -4
x25 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 0 0
x27 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 0 0
x25 x26 x27 x28
x1 0 0 0 0
x2 0 0 0 0
x3 0 0 0 0
x4 0 0 0 0
x5 0 0 0 0
x6 0 0 0 0
x7 0 0 0 0
x8 0 0 0 0
x9 0 0 0 0
x10 0 0 0 0
x11 0 0 0 0
x12 0 0 0 0
x13 0 0 0 0
x14 0 0 0 0
x15 0 0 0 0
x16 0 0 0 0
x17 0 0 0 0
x18 0 0 0 0
x19 0 0 0 0
x20 0 0 0 0
x21 0 0 0 0
x22 0 0 0 0
x23 0 0 0 0
x24 0 0 0 0
x25 -3 3.464 0 0
x26 0 -5 0 0
x27 0 0 -1 1.732
x28 0 0 0 -2
B =
u1 u2 u3 u4 u5 u6 u7 u8
x1 0 0 0 0 0 0 0 0
x2 5.851 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0
x4 2.659 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0
x6 0 3.187 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0
x8 0 2.115 0 0 0 0 0 0
x9 0 0 0 0 0 0 0 0
x10 0 0 4.516 0 0 0 0 0
x11 0 0 0 0 0 0 0 0
x12 0 0 4.061 0 0 0 0 0
x13 0 0 0 0 0 0 0 0
x14 0 0 0 4 0 0 0 0
x15 0 0 0 0 0 0 0 0
x16 0 0 0 4 0 0 0 0
x17 0 0 0 0 0 0 0 0
x18 0 0 0 0 4 0 0 0
x19 0 0 0 0 0 0 0 0
x20 0 0 0 0 4 0 0 0
x21 0 0 0 0 0 0 0 0
x22 0 0 0 0 0 2 0 0
x23 0 0 0 0 0 0 0 0
x24 0 0 0 0 0 4 0 0
x25 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 2 0
x27 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 2 0
u9 u10
x1 0 0
x2 0 0
x3 0 0
x4 0 0
x5 0 0
x6 0 0
x7 0 0
x8 0 0
x9 0 0
x10 0 0
x11 0 0
x12 0 0
x13 0 0
x14 0 0
x15 0 0
x16 0 0
x17 0 0
x18 0 0
x19 0 0
x20 0 0
x21 0 0
x22 0 0
x23 0 0
x24 0 0
x25 0 0
x26 0 0
x27 0 0
x28 0 0
C =
x1 x2 x3 x4 x5 x6 x7
y1 7.264 0.8546 0 0 4.393 1.883 0
y2 0 0 2.632 0.3761 0 0 -1.182
y3 0 0 0 0 0 0 0
y4 0 0 0 0 0 0 0
y5 0 0 0 0 0 0 0
y6 0 0 0 0 0 0 0
y7 0 0 0 0 0 0 0
x8 x9 x10 x11 x12 x13 x14
y1 0 3.321 0.6643 0 0 0 0
y2 2.364 0 0 3.94 0.985 0 0
y3 0 0 0 0 0 4.743 1.5
y4 0 0 0 0 0 0 0
y5 0 0 0 0 0 0 0
y6 0 0 0 0 0 0 0
y7 0 0 0 0 0 0 0
x15 x16 x17 x18 x19 x20 x21
y1 0 0 0 0 0 0 0
y2 0 0 0 0 0 0 0
y3 0 0 3.464 1 0 0 2.121
y4 4.677 1.25 0 0 3 0.75 0
y5 0 0 0 0 0 0 0
y6 0 0 0 0 0 0 0
y7 0 0 0 0 0 0 0
x22 x23 x24 x25 x26 x27 x28
y1 0 0 0 0 0 0 0
y2 0 0 0 0 0 0 0
y3 0.5 0 0 1.732 0.5 0 0
y4 0 2.236 1 0 0 0.866 0.5