Файл: Лабораторная работа 3 по дисциплине Программные средства для анализа и синтеза систем управления Создание объектов типа lti.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
y5 0 0 0 0 0 0 0
y6 0 0 0 0 0 0 0
y7 0 0 0 0 0 0 0
D =
u1 u2 u3 u4 u5 u6 u7 u8 u9 u10
y1 0 0 0 0 0 0 0 0 0 0
y2 0 0 0 0 0 0 0 0 0 0
y3 0 0 0 0 0 0 0 0 0 0
y4 0 0 0 0 0 0 0 0 0 0
y5 0 0 0 0 0 0 0 1 0 0
y6 0 0 0 0 0 0 0 0 1 0
y7 0 0 0 0 0 0 0 0 0 1
Пункт 1.4
SS4 = ss(app4)
SS4 =
A =
x1 x2 x3 x4 x5 x6 x7 x8 x9
x1 -3 4 0 0 0 0 0 0 0
x2 -4 -3 0 0 0 0 0 0 0
x3 0 0 -2 4 0 0 0 0 0
x4 0 0 -4 -2 0 0 0 0 0
x5 0 0 0 0 -4 2 0 0 0
x6 0 0 0 0 -2 -4 0 0 0
x7 0 0 0 0 0 0 -3 3 0
x8 0 0 0 0 0 0 -3 -3 0
x9 0 0 0 0 0 0 0 0 -2
x10 0 0 0 0 0 0 0 0 -4
x11 0 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0 0
x17 0 0 0 0 0 0 0 0 0
x18 0 0 0 0 0 0 0 0 0
x19 0 0 0 0 0 0 0 0 0
x20 0 0 0 0 0 0 0 0 0
x21 0 0 0 0 0 0 0 0 0
x22 0 0 0 0 0 0 0 0 0
x23 0 0 0 0 0 0 0 0 0
x24 0 0 0 0 0 0 0 0 0
x25 0 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 0 0 0
x27 0 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 0 0 0
x10 x11 x12 x13 x14 x15 x16 x17 x18
x1 0 0 0 0 0 0 0 0 0
x2 0 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0 0
x9 4 0 0 0 0 0 0 0 0
x10 -2 0 0 0 0 0 0 0 0
x11 0 -5 2 0 0 0 0 0 0
x12 0 -2 -5 0 0 0 0 0 0
x13 0 0 0 -4 5 0 0 0 0
x14 0 0 0 -5 -4 0 0 0 0
x15 0 0 0 0 0 -3 2 0 0
x16 0 0 0 0 0 -2 -3 0 0
x17 0 0 0 0 0 0 0 -3 2
x18 0 0 0 0 0 0 0 -2 -3
x19 0 0 0 0 0 0 0 0 0
x20 0 0 0 0 0 0 0 0 0
x21 0 0 0 0 0 0 0 0 0
x22 0 0 0 0 0 0 0 0 0
x23 0 0 0 0 0 0 0 0 0
x24 0 0 0 0 0 0 0 0 0
x25 0 0 0 0 0 0 0 0 0
x26 0 0 0 0 0 0 0 0 0
x27 0 0 0 0 0 0 0 0 0
x28 0 0 0 0 0 0 0 0 0
x19 x20 x21 x22 x23 x24 x25 x26 x27
x1 0 0 0 0 0 0 0 0 0
x2 0 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0 0
x9 0 0 0 0 0 0 0 0 0
x10 0 0 0 0 0 0 0 0 0
x11 0 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0 0
x17 0 0 0 0 0 0 0 0 0
x18 0 0 0 0 0 0 0 0 0
x19 -1 3 0 0 0 0 0 0 0
x20 -3 -1 0 0 0 0 0 0 0
x21 0 0 -3 3 0 0 0 0 0
x22 0 0 -3 -3 0 0 0 0 0
x23 0 0 0 0 -4 4 0 0 0
x24 0 0 0 0 -4 -4 0 0 0
x25 0 0 0 0 0 0 -1 1 0
x26 0 0 0 0 0 0 -1 -1 0
x27 0 0 0 0 0 0 0 0 -1
x28 0 0 0 0 0 0 0 0 -2
x28
x1 0
x2 0
x3 0
x4 0
x5 0
x6 0
x7 0
x8 0
x9 0
x10 0
x11 0
x12 0
x13 0
x14 0
x15 0
x16 0
x17 0
x18 0
x19 0
x20 0
x21 0
x22 0
x23 0
x24 0
x25 0
x26 0
x27 2
x28 -1
B =
u1 u2 u3 u4 u5
x1 0 0 0 0 0
x2 2.991 0 0 0 0
x3 0 0 0 0 0
x4 2.991 0 0 0 0
x5 0 0 0 0 0
x6 3.557 0 0 0 0
x7 0 0 0 0 0
x8 2.582 0 0 0 0
x9 0 0 0 0 0
x10 0 3.138 0 0 0
x11 0 0 0 0 0
x12 0 3.557 0 0 0
x13 0 0 0 0 0
x14 0 3.449 0 0 0
x15 0 0 0 0 0
x16 0 5.318 0 0 0
x17 0 0 0 0 0
x18 0 0 5.851 0 0
x19 0 0 0 0 0
x20 0 0 2.659 0 0
x21 0 0 0 0 0
x22 0 0 0 3.187 0
x23 0 0 0 0 0
x24 0 0 0 2.115 0
x25 0 0 0 0 0
x26 0 0 0 0 4.516
x27 0 0 0 0 0
x28 0 0 0 0 4.061
C =
x1 x2 x3 x4 x5 x6
y1 1.337 0.6687 0 0 0 0
y2 0 0 1.337 0.6687 0 0
y3 0 0 0 0 1.687 0.5623
y4 0 0 0 0 0 0
y5 0 0 0 0 0 0
y6 0 0 0 0 0 0
x7 x8 x9 x10 x11 x12
y1 0 0 2.151 0.9559 0 0
y2 0 0 0 0 5.061 1.687
y3 0 0 0 0 0 0
y4 1.549 1.162 0 0 0 0
y5 0 0 0 0 0 0
y6 0 0 0 0 0 0
x13 x14 x15 x16 x17 x18
y1 0 0 0 0 0 0
y2 0 0 0 0 0 0
y3 2.436 0.8699 0 0 0 0
y4 0 0 2.632 0.3761 0 0
y5 0 0 0 0 7.264 0.8546
y6 0 0 0 0 0 0
x19 x20 x21 x22 x23 x24
y1 0 0 0 0 0 0
y2 0 0 0 0 0 0
y3 0 0 0 0 0 0
y4 0 0 0 0 0 0
y5 0 0 4.393 1.883 0 0
y6 2.632 0.3761 0 0 -1.182 2.364
x25 x26 x27 x28
y1 0 0 0 0
y2 0 0 0 0
y3 0 0 0 0
y4 0 0 0 0
y5 3.321 0.6643 0 0
y6 0 0 3.94 0.985
D =
u1 u2 u3 u4 u5
y1 0 0 0 0 0
y2 0 0 0 0 0
y3 0 0 0 0 0
y4 0 0 0 0 0
y5 0 0 0 0 0
y6 0 0 0 0 0
3 Используя команду ss2ss(sys2,T) перейти к альтернативной ss-форме. Матрицы перехода Т сгенерировать генератором случайных чисел rand.
3 Выполнение
SYS2 = ss(sys2)
С помощью SYS2.A определили размерность матрицы SYS2 для перехода Т
T=rand(12);
sysT = ss2ss(SYS2,T)
sysT =
A =
x1 x2 x3 x4
x1 -17.9 6.928 11.62 -5.625
x2 -21.83 11.63 10.33 -11.23
x3 -30.4 17.74 15.02 -12.06
x4 -21.19 15.99 9.839 -7.433
x5 -8.48 9.999 0.1764 3.18
x6 -31.55 22 13.97 -13.17
x7 -3.273 5.755 1.791 4.063
x8 -28.06 20.91 13.27 -10.29
x9 -26.44 25.49 6.815 -5.005
x10 -20.9 17.08 8.573 -9.648
x11 2.613 4.498 -5.871 8.127
x12 -20.5 14.23 7.867 -5.357
x5 x6 x7 x8
x1 -8.339 0.1829 7.059 11.45
x2 -13.4 2.137 9.705 27.81
x3 -17.46 2.499 12.46 32
x4 -13.87 0.5645 9.24 22.79
x5 -6.555 -2.341 4.255 10.31
x6 -23.6 0.4077 13.89 40.54
x7 -3.704 -4.82 1.538 0.9841
x8 -19.47 2.037 12.96 33.1
x9 -18.1 -0.02729 11.34 35.79
x10 -15.86 1.619 10.41 30.16
x11 1.683 -6.43 3.441 -3.512
x12 -11.42 -0.4247 8.796 25.37
x9 x10 x11 x12
x1 0.8096 -22.14 5.416 -0.5673
x2 3.547 -40.4 7.616 -4.385
x3 3.344 -52.08 11.02 -5.4
x4 2.275 -37.93 6.869 -4.267
x5 -0.00525 -19.12 1.464 -0.139
x6 7.001 -60.99 9.42 -4.973
x7 1.135 -8.015 -1.431 1.198
x8 5.453 -56.07 9.218 -6.938
x9 2.937 -56.86 7.526 -5.706
x10 5.896 -47.08 6.424 -6.598
x11 -0.3199 3.85 -5.776 0.2528
x12 2.828 -37.2 6.241 -5.897
B =
u1 u2 u3
x1 1.077 0.9164 7.389
x2 2.266 2.772 4.19
x3 2.652 3.807 7.512
x4 5.21 3.45 3.001
x5 3.766 2.48 3.199
x6 6.074 2.723 2.02
x7 6.366 2.077 5.965
x8 1.533 4.407 5.062
x9 6.928 4.852 0.9273
x10 1.991 3.73 2.536
x11 4.749 1.518 3.478
x12 4.92 2.117 3.795
C =
x1 x2 x3 x4 x5 x6
y1 54.68 -26.94 -25.5 28.96 38.59 -6.867
y2 -25.34 17.35 8.016 -14.94 -24.89 5.26
x7 x8 x9 x10 x11 x12
y1 -23.22 -66.66 -7.334 93.1 -16.69 3.061
y2 12.49 44.63 8.353 -58.46 8.167 -4.243
D =
u1 u2 u3
y1 0 0 0
y2 0 0 0
4 Преобразовать полученные в задании 3 системы в zpk-форму. Сравнить передаточные функции систем с передаточными функциями систем, полученных в пп. 1.4 и 1.5.
4 Выполнение
SYSt = zpk(sysT)
SYSt =
From input 1 to output...
5 (s+20) (s^2 + 2s + 2) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
1: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
(s+22) (s^2 + 2s + 2) (s^2 + 6s + 13)
(s^2 + 2s + 5) (s^2 + 6s + 18)
(s^2 + 8s + 32)
2: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
From input 2 to output...
6 (s+10) (s^2 + 2s + 2) (s^2 + 6s + 13)
(s^2 + 2s + 5) (s^2 + 2s + 10)
(s^2 + 8s + 32)
1: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
5 (s+2) (s^2 + 2s + 2) (s^2 + 2s + 5)
(s^2 + 6s + 13) (s^2 + 2s + 10)
(s^2 + 6s + 18)
2: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
From input 3 to output...
3 (s+6) (s^2 + 2s + 5) (s^2 + 6s + 13)
(s^2 + 2s + 10) (s^2 + 6s + 18)
(s^2 + 8s + 32)
1: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
4 (s+9) (s^2 + 2s + 2) (s^2 + 6s + 13)
(s^2 + 2s + 10) (s^2 + 6s + 18)
(s^2 + 8s + 32)
2: -----------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5)
(s^2 + 6s + 18) (s^2 + 2s + 10)
(s^2 + 8s + 32)
>>QC41 = zpk(qc41);
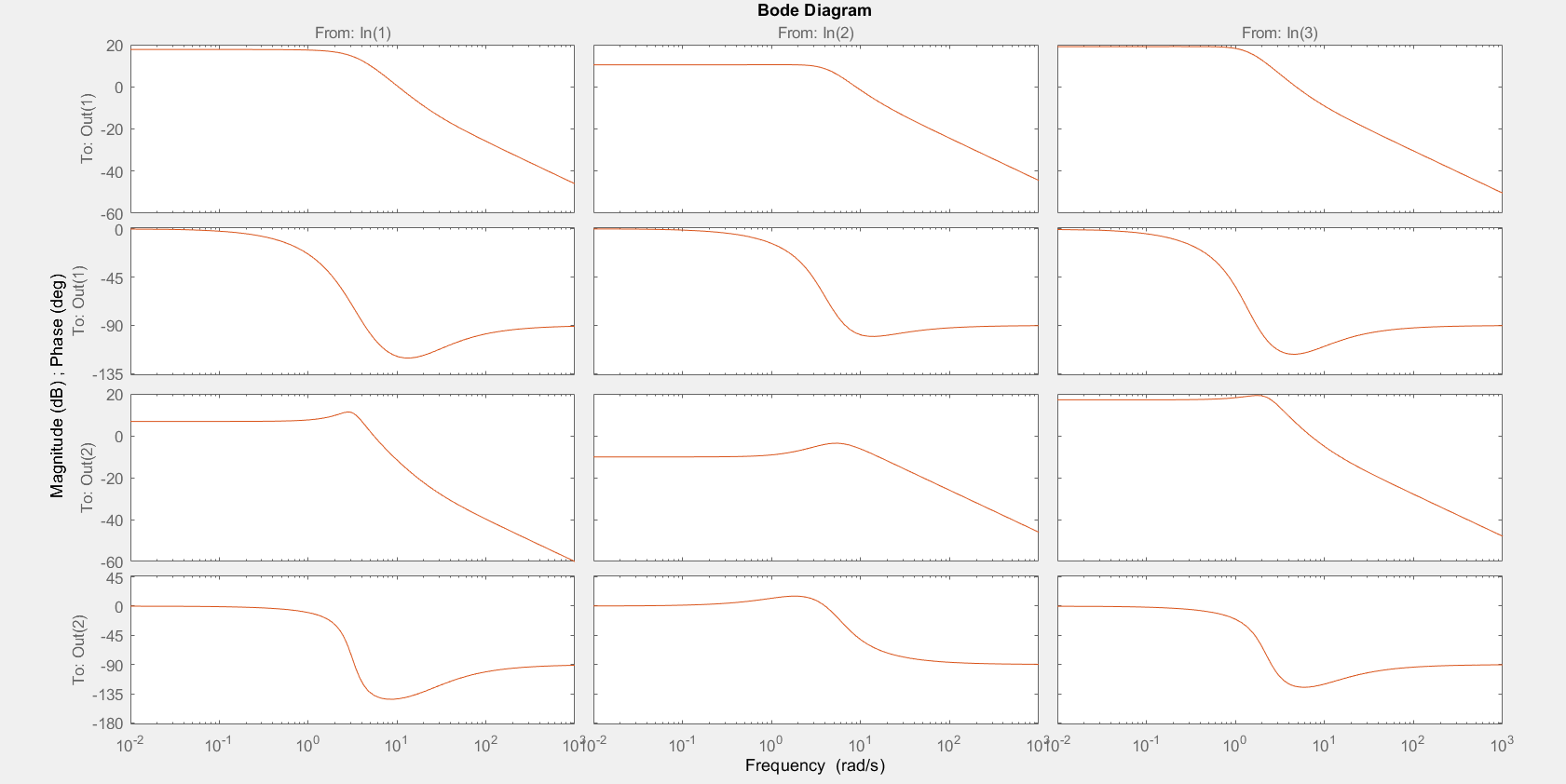
>> bode(QC41,SYSt)
>> sys2=ss(sys2);
>> sys2.A
ans =
-3 2 0 0 0 0 0 0 0 0 0 0
-2 -3 0 0 0 0 0 0 0 0 0 0
0 0 -1 3 0 0 0 0 0 0 0 0
0 0 -3 -1 0 0 0 0 0 0 0 0
0 0 0 0 -3 3 0 0 0 0 0 0
0 0 0 0 -3 -3 0 0 0 0 0 0
0 0 0 0 0 0 -4 4 0 0 0 0
0 0 0 0 0 0 -4 -4 0 0 0 0
0 0 0 0 0 0 0 0 -1 1 0 0
0 0 0 0 0 0 0 0 -1 -1 0 0
0 0 0 0 0 0 0 0 0 0 -1 2
0 0 0 0 0 0 0 0 0 0 -2 -1
>> T = rand(12);
>> sysT = ss2ss(sys2,T);
>> bode(sys2,sysT)
>> zpk(sys2)
ans =
From input 1 to output...
5 (s+20)
1: ---------------
(s^2 + 6s + 13)
(s+22)
2: ---------------
(s^2 + 2s + 10)
From input 2 to output...
6 (s+10)
1: ---------------
(s^2 + 6s + 18)
5 (s+2)
2: ---------------
(s^2 + 8s + 32)
From input 3 to output...
3 (s+6)
1: --------------
(s^2 + 2s + 2)
4 (s+9)
2: --------------
(s^2 + 2s + 5)
Continuous-time zero/pole/gain model.
>> zpk(sysT)
ans =
From input 1 to output...
5 (s+20) (s^2 + 2s + 2) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
1: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
(s+22) (s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 8s + 32)
2: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
From input 2 to output...
6 (s+10) (s^2 + 2s + 2) (s^2 + 2s + 5) (s^2 + 6s + 13) (s^2 + 2s + 10) (s^2 + 8s + 32)
1: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
5 (s+2) (s^2 + 2s + 2) (s^2 + 2s + 5) (s^2 + 6s + 13) (s^2 + 2s + 10) (s^2 + 6s + 18)
2: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
From input 3 to output...
3 (s+6) (s^2 + 2s + 5) (s^2 + 6s + 13) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
1: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
4 (s+9) (s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
2: ---------------------------------------------------------------------------------------------
(s^2 + 2s + 2) (s^2 + 6s + 13) (s^2 + 2s + 5) (s^2 + 6s + 18) (s^2 + 2s + 10) (s^2 + 8s + 32)
>> minreal(zpk(sysT))
ans =
From input 1 to output...
5 (s+20)
1: ---------------
(s^2 + 6s + 13)
(s+22)
2: ---------------
(s^2 + 2s + 10)
From input 2 to output...
6 (s+10)
1: ---------------
(s^2 + 6s + 18)
5 (s+2)
2: ---------------
(s^2 + 8s + 32)
From input 3 to output...
3 (s+6)
1: --------------
(s^2 + 2s + 2)
4 (s+9)
2: --------------
(s^2 + 2s + 5)