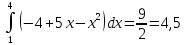Добавлен: 25.10.2023
Просмотров: 46
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В задачах 1 – 10 найти указанные пределы.
4.
а)
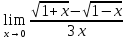
Неопределенность
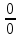
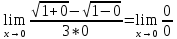
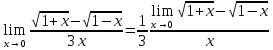
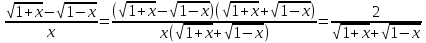
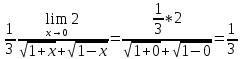
Найденный предел
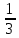
б)
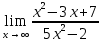
Неопределенность
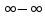
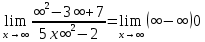
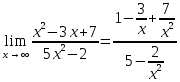
Сокращаем слагаемые
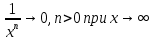
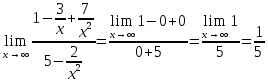
Найденный предел
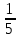
в)
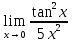
Неопределенность
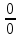
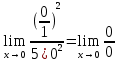
Применяем формулу
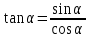
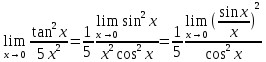
Первый замечательный предел
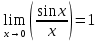
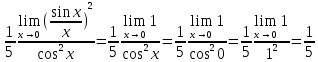
Найденный предел
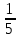
В задачах 11 – 20 для каждой из заданных функций найти точки разрыва и исследовать их характер
14.
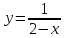
Исследуем данную функцию на непрерывность:
Найдем точки разрыва функции внутри указанной области.
Разрывы
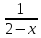являются нулями 2-xх при которых (2-х=0; х=2)
Находим переделы в точке x=2
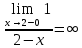
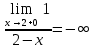
В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Ответ: Точка x1=2 является точкой разрыва II-го рода.
В задачах 21 – 30 найти производные заданных функций.
24.
а)
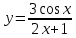
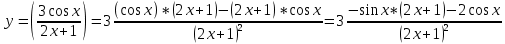
б)
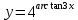
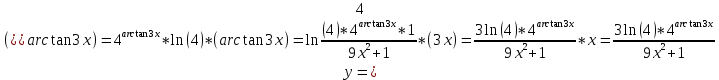
В задачах 31 – 40 исследовать данные функции методами дифференциального исчисления и построить их графики
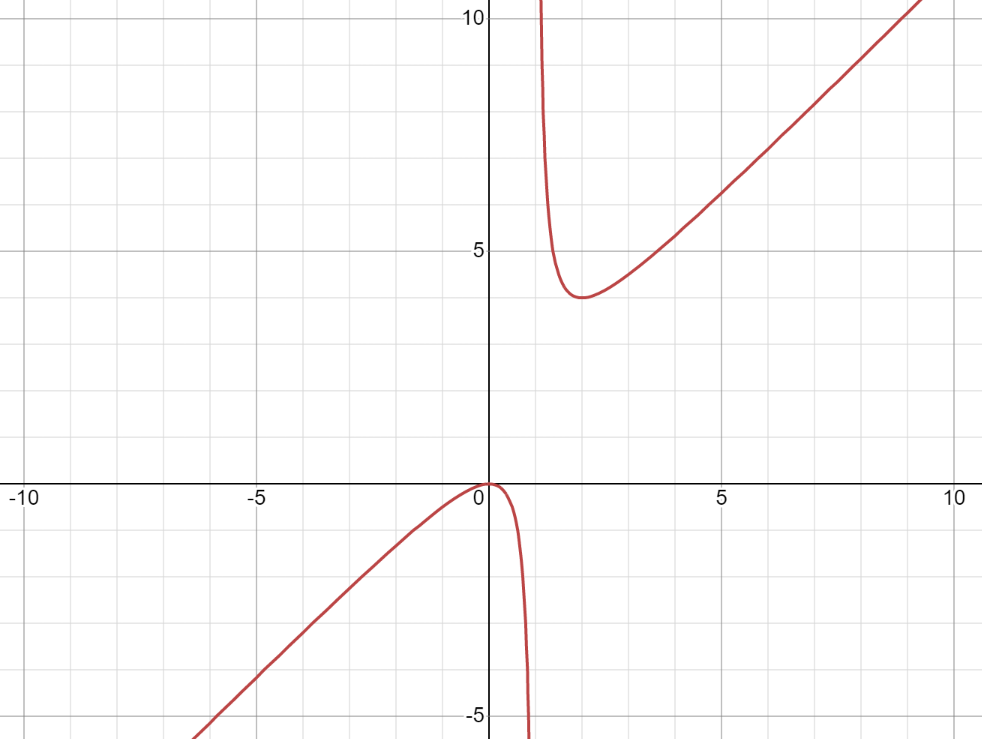
34.
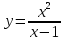
1) Область определения функции
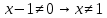
D(y)=(−∞;1) ∪ (1; +∞)
2) Множество значений
Е(х)= (0 ; ∞)
3) Проверим является ли функция четной или нечетной
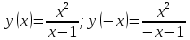
Т.к.
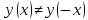и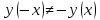 
, то функция не является ни четной ни не четной.4) Нули функции
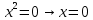
5) Промежутки знакопостоянства
    |
| 0 1 |
6) Возрастание, убывание
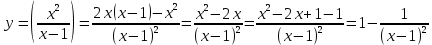
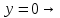
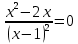
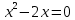
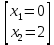
Получили 2 стационарные точки, проверим их на экстремум:
Так как на промежутках (- ∞; 0) U (2; ∞) y`>0, то на этих промежутках функция возрастает.
Так как на промежутках (0; 1] U [1; 2) у`< 0, то на этих промежутках функция убывает.
Промежутки:
       |
| 0 1 2 |
    |
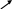Точка х=0 является точкой максимума у (0)=0
Точка х=2 является точкой минимума у (2)=4
7) Выпуклость, вогнутость и точки перегиба функции
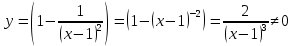
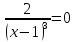, уравнение не имеет корней, следовательно, точек перегиба функция не имеет. Т.к. на промежутке (1; ∞) , y`> 0, то на этом промежутке график функции направлен выпуклостью вниз.
Т.к. на промежутке (- ∞; 1) y`< 0 то на этом промежутке график функции направлен выпуклостью вверх
| |
| 1 |
  |
8) Наклонные асимптоты
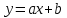
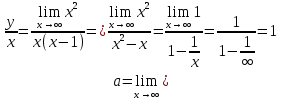
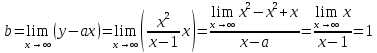
Получаем: y=x+1 – наклонная асимптота
В задачах 41 – 50 найти неопределенные интегралы.
44.
а)
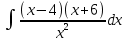
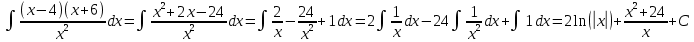
б)
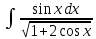
Подстановка
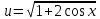
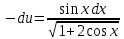
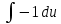
Интеграл от константы
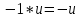
Обратная замена
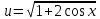
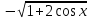
В задачах 51 – 60 вычислить определенные интегралы.
54.
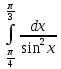
Функция непрерывна на интервале
По формуле:
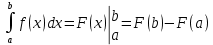
Где
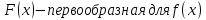
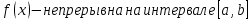
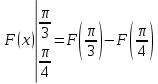
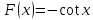
Значения
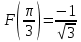
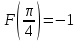
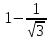
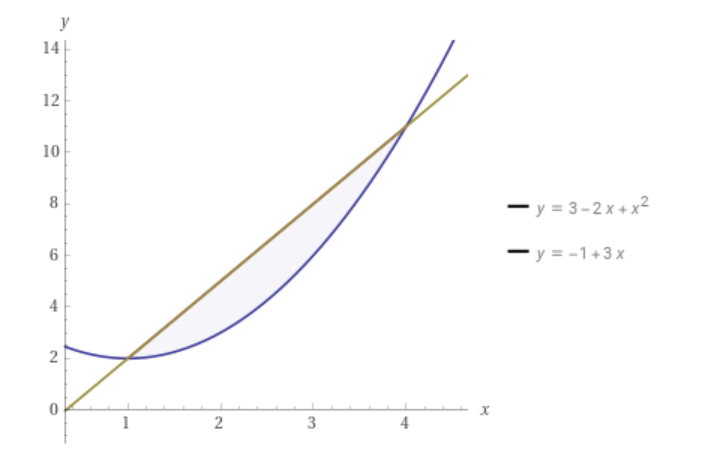
В задачах 61 – 70 найти площади фигуры, ограниченных линиями. Сделать чертеж
64.
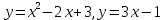
Площадь:
