Файл: Контрольная работа по дисциплине Методы и средства исследований Вариант 6 Автор Т. Н. Ильченко подпись, дата инициалы, фамилия.doc

Детали готового кроя нумеруются путем пришивания купонов на машинке, разметки краской или записи карандашом или мелом. Пучки отрезанных деталей из основной ткани и пучки отрезанной подкладки и приклада завершаются и связываются вместе. Отрез поступает на хранение на склад кроя, откуда по мере необходимости отправляется в швейные мастерские.В раскройном цехе они составляют документ для маршрута раскроя.Маршрут-лист - это документ, который сопровождает пачку отрезов всех деталей из основной ткани, подкладки и торца изделий одинакового размера из раскройного цеха на склад готовой продукции и служит отчетным документом при передаче отреза, полуфабрикатов и готовой продукции на производственные площадки (семинары). Маршрут заполняется на основании выданной карточки расчета материалов. В нем записываются все данные, характеризующие разрезанный пакет, указывается, для кого предназначен разрез, а также сообщаются все выходные данные готового продукта.Вариант 2соответствует последней цифре № зачетной книжки студента: 5,6,7,8,9При оценке фильтрационной способности пакетов одежды с ветрозащитной прокладкой были получены следующие цифры, характеризующие величину расхода воздуха: 2920; 2890; 2830; 2870; 2920; 2750; 2870; 2940; 3010; 2910 (дм³/с).Задача 1. Проверьте гипотезу об отсутствии ухода систематической погрешности (оцените, не происходит ли изменений в показаниях прибора). Уровень значимости α = 0,05%.Используем критерий инверсий ([1], с. 100, 111)Представим результаты в виде:

2920	2890	2830	2870	2920	2750	2870	2940	3010	2910
x1	x2	x3	x4	x5	x6	x7	x8	x9	x10

Полученную последовательность исследуем для каждого

---

x_i на наличие инверсий: для x₁>x₉………………………………………………………………. A₁=1;для x₂>x₉……………………………………………………………… A₂=1;для x₃>x₇; x₃>x₈; x₃>x₉……………………………………………….. A₃=3;для x₄>x₅; x₄>x₇; x₄>x₈; x₄>x₉; x₄……………. ………………… A₄=7;для x₅>x₇; x₅>x₈; x₅>x₉; x₅>x₁₀……………………………………….. A₅=4;для x₆>x₇; x₆>x₈; x₆>x₉; x₆>x₁₀; x₆…………………….. ……….. A₆=8;для x₇>x₉………………………………………………………………. A₇=1;для x₈>x₉………………………………………………………………. A₈=1;для x₉>x_γ ……………………………………………………………… A₉=0;для x₁₀>……………… ……….………………………………..... A₁₀=3;Общее число инверсий По табл. П4 (см. [1]) находим для числа измерений n=14 и критического уровня α=0,05 интервал А_нижн и А_верх, который составляет 27<А<63. Полученное значение А=31 попадает в указанный интервал, а это значит ­– нет ухода систематической погрешности.Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально распределенной величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию ,где – выборочная средняя, а₀ – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с степенями свободы.Требуется найти критическую область для нулевой гипотезы Н₀: а₀=0,05 при альтернативной гипотезе Н₁: а₁<2900. Очевидно, что другие альтернативные гипотезы (

---

и ) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.

Критическая область левосторонняя; находим из условия .

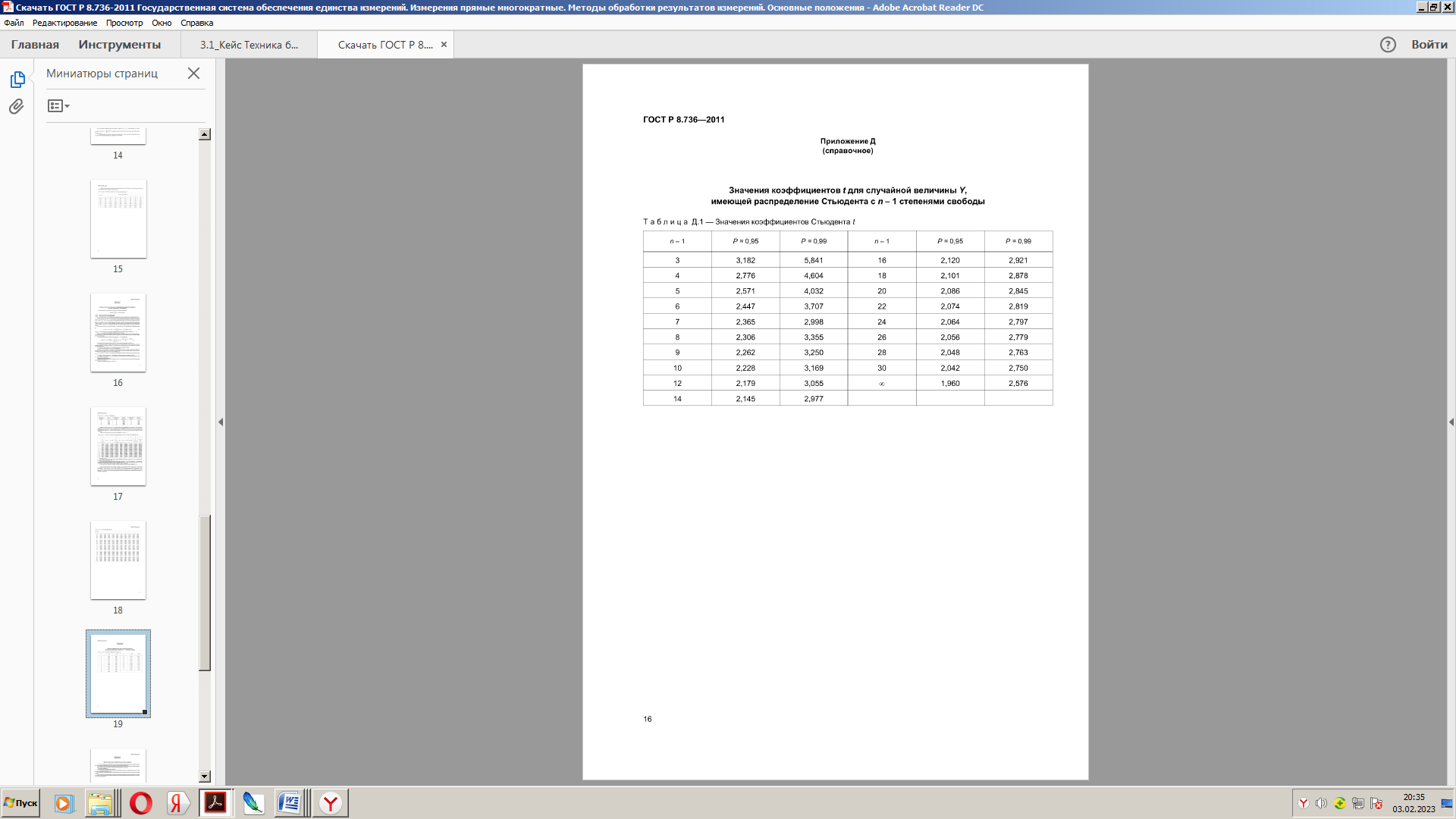
Задача 2. Определите, имеются ли грубые погрешности (выбросы) среди результатов многократных измерений, указанных в задаче № 1, при доверительной вероятности Р = 0,95 (95%), используя Критерий Граббса.

Расчеты выполнить с использованием Microsoft Office Excel
Следует проверить, является ли эта погрешность систематической.



С -доверительный интервал концентраций.

S - стандартное отклонение, рассчитанное из 20 параллельных измерений концентрации

f - коэффициент Стъюдента, при Р=0,95, n=20

Разность среднего результата анализа и паспортного значения концентрации стандартного образца, взятого для исследования, больше доверительного интервала. Следовательно, методика отягощена систематической погрешностью.


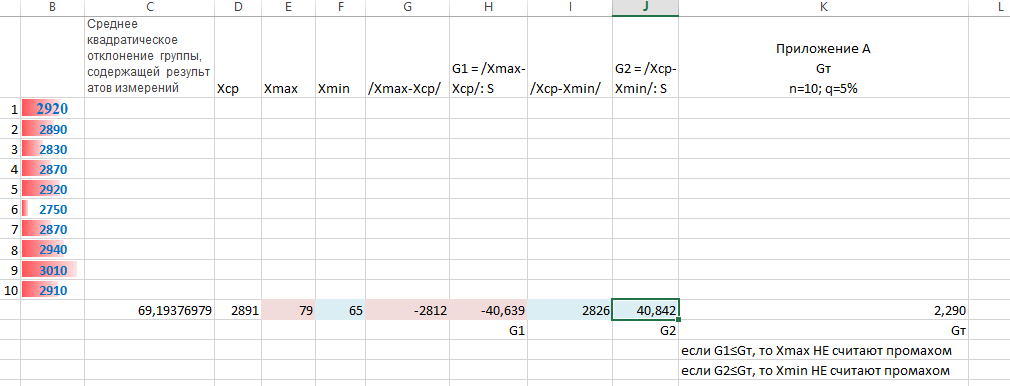
Задача 3. Для выборки, приведенной в задаче № 1 с учетом удаления выбросов, определите случайную погрешность результатов измерений при доверительной вероятности Р = 0,95.

Расчеты выполнить с использованием Microsoft Office Excel

Представить методику расчета , S, , и выбор t - коэффициент Стьюдента
Доверительные границы случайной погрешности вычисляются при доверительной вероятности P = 0,95, а также при P = 0,99, если измерения в дальнейшем повторить нельзя:



где t_p – коэффициент Стьюдента, определяемый по табл. П.4 при заданной доверительной вероятности P и числе степеней свободы k. Для прямых измерений

---

литература

1. 
   Веселов, В.В. Методы и средства исследований: учебник / В.В. Веселов, А.А. Виноградов, С.В. Королева. – Иваново: ИГТА, 2009. -340 с.
   
2. 
   Сафронова, И.В. Технические методы и средства измерений в швейной промышленности. - М.: Легкая и пищевая промышленность, 1983.-232с.
   
3. 
   Кузьмичев В.Е., Козырев В.В. Практикум по методам и
   средствам исследований в швейном производстве. - Иваново, ИГТА 1997.- 108с. /2084 в библиотеке ИГТА/
   
4. 
   Веселов В.В., Колотилова Г.В. Методы и средства исследований технологических процессов швейного производства: Учебное пособие.- Иваново; ИвТИ, 1983/№ 1030 в библиотеке ИГТА/.
   
5. 
   Кузьмичёв, В.Е. Методы и средства исследований химических процессов в швейном производстве: учеб. пособие / В.Е. Кузьмичёв, В.В. Веселов, Г.В. Колотилова.- Иваново: ИХТИ, 1986.-96с. /1340 в библиотеке ИГТА/.
   

ПРИЛОЖЕНИЯ

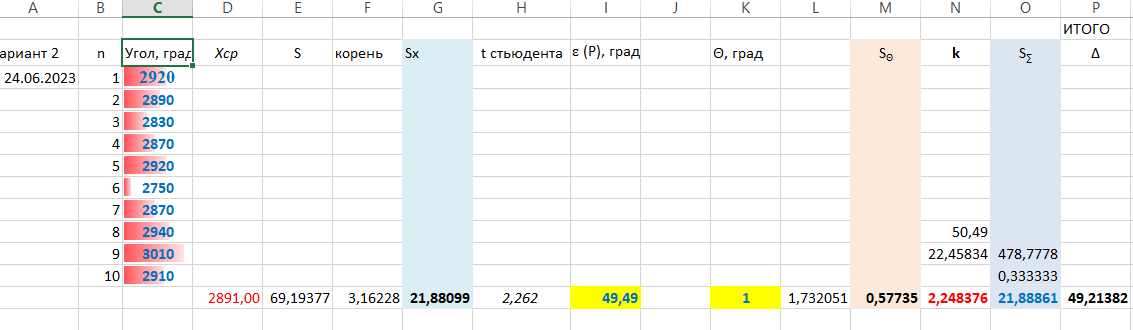
Границы А_нижн и А_верхн интервалов для числа инверсий при определении изменения во времени систематической погрешности

Число измерений (объем выработки) n	Границы интервала для заданного уровня значимости
	α = 0,1 (10 %)		α =0,05 (5 %)
	Анижн	Аверх	Анижн	Аверх
10	13	31	11	33
14	30	60	27	63
20	69	120	64	125
30	171	263	162	272
50	756	1013	731	1038
70	1045	1369	1014	1400
100	2198	2751	2145	2804

---