В экономической системе выделены 8 отраслей:

1. Машиностроение

2. Химическая промышленность

3. Недропользование

4. Легкая промышленность

5. Транспорт и связь

6. Электроэнергетика

7. Металлургическая промышленность

8. Сельское хозяйство

Матрица коэффициентов прямых затрат A имеет вид

0.15	0.08	0.05	0.09	0.03	0.09	0.01	0.04
0.06	0.15	0.01	0.09	0.05	0.07	0.05	0.06
0.09	0.06	0.19	0.04	0.04	0.19	0.09	0.03
0.05	0.11	0.04	0.19	0.05	0.08	0.07	0.05
0.08	0.08	0.11	0.06	0.17	0.10	0.05	0.05
0.11	0.06	0.07	0.05	0.04	0.16	0.11	0.07
0.10	0.08	0.01	0.07	0.07	0.09	0.19	0.06
0.01	0.05	0.06	0.19	0.05	0.04	0.07	0.18

---

Вектор конечной продукции Y

350
350
410
240
290
510
420
270

Решением задачи является вектор X, который находится путем умножения обратной матрицы (E-A) умноженная на Y, где E – единичная матрица.

Найдем:

матрицу Е – А

0.85	-0.08	-0.05	-0.09	-0.03	-0.09	-0.01	-0.04
-0.06	0.85	-0.01	-0.09	-0.05	-0.07	-0.05	-0.06
-0.09	-0.06	0.81	-0.04	-0.04	-0.19	-0.09	-0.03
-0.05	-0.11	-0.04	0.81	-0.05	-0.08	-0.07	-0.05
-0.08	-0.08	-0.11	-0.06	0.83	-0.10	-0.05	-0.05
-0.11	-0.06	-0.07	-0.05	-0.04	0.84	-0.11	-0.07
-0.10	-0.08	-0.01	-0.07	-0.07	-0.09	0.81	-0.06
-0.01	-0.05	-0.06	-0.19	-0.05	-0.04	-0.07	0.82

---

Обратную матрицу E-A = (E-A)^-1 = B

1.276	0.206	0.140	0.235	0.109	0.239	0.115	0.132
0.175	1.283	0.089	0.241	0.136	0.210	0.163	0.158
0.273	0.227	1.338	0.219	0.154	0.426	0.266	0.157
0.189	0.268	0.140	1.376	0.153	0.254	0.211	0.164
0.246	0.245	0.249	0.241	1.298	0.311	0.204	0.174
0.271	0.213	0.185	0.226	0.145	1.355	0.266	0.193
0.256	0.238	0.109	0.250	0.182	0.271	1.350	0.182
0.140	0.205	0.171	0.399	0.158	0.214	0.220	1.316

Элементы матрицы B называются коэффициентами полных материальных затрат. Они показывают величину производственных затрат в i-той отрасли, которые необходимы для получения единицы конечной продукции в j-той отрасли. Полные затраты включают в себя сумму

---

прямых и косвенных затрат, т.е. затрат более высоких порядков, которые могут быть выявлены через ряд технологических звеньев. Как правило косвенные затраты могут быть оценены лишь приближенно, поэтому коэффициенты полных затрат имеют большое практическое значение, так как позволяют определить, как повлияет изменение величины конечной продукции отрасли на функционирование экономической системы в целом.
Вектор совокупного общественного продукта B*Y = X

X1	870.0503
X2	861.5969
X3	1192.366
X4	854.411
X5	999.1968
X6	1196.606
X7	1084.785
X8	889.5359

Это значит, что для достижения заданных величин конечных общественных продуктов совокупный общественный продукт в машиностроении должен составлять (x1) – 870.0503; в химической промышленности (х2) – 861.5969; в недропользовании (х3) – 1192.366; в легкой промышленности (х4) - 854.411; в транспорте и связи (х5) – 999.1968; в электроэнергетике (х6) – 1196.606; в металлургической промышленности (х7) – 1084.785; в сельском хозяйстве (х8) – 889.5359.

Далее сравним различные технологии производства продуктов и ликвидации отходов по соответствующему им вектору выпуска загрязнителей, а также определять суммарные затраты отраслей на природоохранные мероприятия.

ɣ = 0,09 (для Ã 1 + 0,08)

ΔA = ɣ * A

ΔA = 0.1 * A

A(1+ ɣ) = Ã

Ã=ɣ*A

0.1635	0.0872	0.0545	0.0981	0.0327	0.0981	0.0109	0.0436
0.0654	0.1635	0.0109	0.0981	0.0545	0.0763	0.0545	0.0654
0.0981	0.0654	0.2071	0.0436	0.0436	0.2071	0.0981	0.0327
0.0545	0.1199	0.0436	0.2071	0.0545	0.0872	0.0763	0.0545
0.0872	0.0872	0.1199	0.0654	0.1853	0.109	0.0545	0.0545
0.1199	0.0654	0.0763	0.0545	0.0436	0.1744	0.1199	0.0763
0.109	0.0872	0.0109	0.0763	0.0763	0.0981	0.2071	0.0654
0.0109	0.0545	0.0654	0.2071	0.0545	0.0436	0.0763	0.1962

---

Матрица коэффициентов прямых затрат учитывая экологические затраты

E-Ã

0.8365	-0.0872	-0.0545	-0.0981	-0.0327	-0.0981	-0.0109	-0.0436
-0.0654	0.8365	-0.0109	-0.0981	-0.0545	-0.0763	-0.0545	-0.0654
-0.0981	-0.0654	0.7929	-0.0436	-0.0436	-0.2071	-0.0981	-0.0327
-0.0545	-0.1199	-0.0436	0.7929	-0.0545	-0.0872	-0.0763	-0.0545
-0.0872	-0.0872	-0.1199	-0.0654	0.8147	-0.109	-0.0545	-0.0545
-0.1199	-0.0654	-0.0763	-0.0545	-0.0436	0.8256	-0.1199	-0.0763
-0.109	-0.0872	-0.0109	-0.0763	-0.0763	-0.0981	0.7929	-0.0654
-0.0109	-0.0545	-0.0654	-0.2071	-0.0545	-0.0436	-0.0763	0.8038

Теперь находим обратную матрицу (E-Ã)^-1=

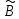
1.339575	0.264471	0.180475	0.302539	0.144624	0.308309	0.161364	0.174236
0.228244	1.348505	0.12384	0.308943	0.175021	0.274724	0.214029	0.203444
0.35506	0.304044	1.411545	0.302313	0.205747	0.535847	0.345356	0.214834
0.251463	0.340776	0.186478	1.467077	0.199171	0.333611	0.276056	0.216058
0.321706	0.321731	0.312297	0.32383	1.363043	0.405185	0.273567	0.231427
0.345113	0.283212	0.238142	0.304307	0.191982	1.449189	0.339379	0.250277
0.328404	0.310247	0.153639	0.330744	0.233102	0.354446	1.430349	0.237561
0.199025	0.274185	0.222415	0.4975	0.206844	0.292087	0.288657	1.385212

---

Смотрите также файлы

• Нефтяной институт.docx

• Сущность понятия духовнонравственного воспитания.docx

• ыса мерзімді саба жоспары дістемелік бірлестік жетекшісіні атыжні.docx

• Кафедра Строительство, архитектура и дизайн отчёт по учебной практике (изыскательская практика).docx

• Планконспект. Ход занятия учебные вопросы и время Действия руководителя Действия обучаемых.docx