ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 41
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание № 1
по учебному курсу «»
(наименование учебного курса)
Вариант 5.5
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Запишем исходные данные расчетной электрической цепи тока.
Источник входного напряжения (рис. 1):
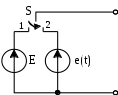
Рис. 1. Источник входного напряжения
Нагрузка (рис. 2)
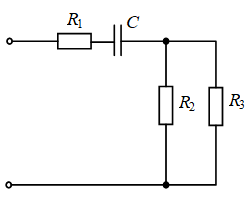
Рис. 2. Нагрузка
Сопротивление резисторов:
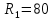 Ом,
Ом, 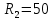 Ом,
Ом, 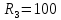
Ом. Величина ёмкости
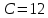 мкФ. Значения источника электрической энергии:
мкФ. Значения источника электрической энергии: 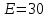 В,
В, 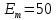 В,
В,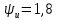 рад = 103,1324 ̊ , ω = 220 рад/с.
рад = 103,1324 ̊ , ω = 220 рад/с.Объединим схемы на рисунках 1 и 2 в одну (рис. 3).
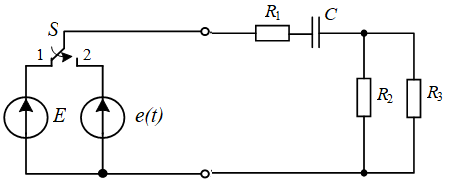
Рис. 3. Исходная схема для расчета цепи
Проанализируем исходную схему (рис. 3). До коммутации к нагрузке было подключено постоянное напряжение Е. В момент коммутации ключ из положения 1 переключается в положение 2 на источник переменного напряжение e(t). Через нагрузку начинает протекать переменное напряжение.
Найдем докоммутационные значения токов и напряжений. До коммутации источник переменного напряжения отключен от цепи, поэтому можно его временно удалить из схемы (рис. 4).
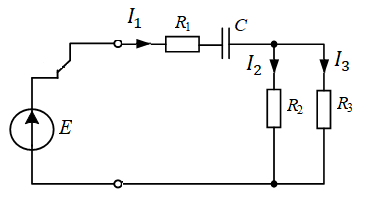
Рис. 4. Докоммутационная схема для расчета цепи
Анализ схемы (рис. 4) показывает, что электрическая цепь содержит 2 контура. В этих контурах присутствуют источник постоянного напряжения E, активные сопротивления
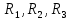 и емкость С. На постоянном токе емкостное сопротивление равно бесконечности. Бесконечность – это разрыв в цепи (рис. 5).
и емкость С. На постоянном токе емкостное сопротивление равно бесконечности. Бесконечность – это разрыв в цепи (рис. 5). 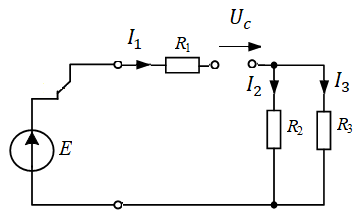
Рис. 5. Эквивалентная докоммутационная схема для расчета цепи
Токи цепи равны 0 , пскольку цепь разорвана эквивалентным сопротивлением конденсатора (формула 1)
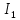 =
= 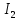 =
= 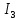 = 0 (1)
= 0 (1)Напряжение конденсатора (формула 2):
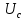 =
= 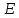 = 30 (B) (2)
= 30 (B) (2)Напряжения резисторов согласно закона Ома (формулы 3..5):
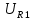
=
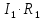 = 0
= 0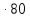 = 0 (3)
= 0 (3)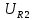 =
= 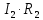 = 0
= 0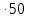 = 0 (4)
= 0 (4)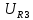 =
= 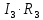 = 0
= 0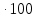 = 0 (5)
= 0 (5)Запишем данные в таблицу 1.
Таблица 1
 (0-), A (0-), A | 0 |
 (0-), B (0-), B | 0 |
 (0-), A (0-), A | 0 |
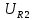 (0-), B (0-), B | 0 |
 (0-), A (0-), A | 0 |
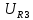 (0-), B (0-), B | 0 |
 (0-), B (0-), B | 30 |
Независимыми начальными значениями являются ток в катушке индуктивности и напряжение на конденсаторе. В нашей схеме присутствует только конденсатор. Значит, независимым начальным значением будет только напряжение на конденсаторе (формула 6):
 = 30 (В). (6)
= 30 (В). (6)Рассчитаем значения в момент коммутации при t = 0+. В момент коммутации ключ S переключается из положения 1 в положение 2 (рис. 6). При этом источник постоянного напряжения Е отключается и подключается источник переменного напряжения e(t). В результате упрощенная схема будет выглядеть, как на рисунке 6.
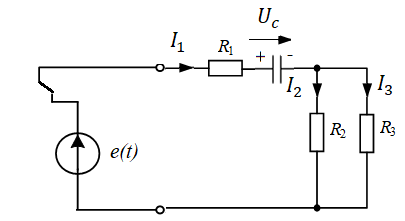
Рис. 6. Электрическая цепь в момент коммутации
Конденсатор до коммутации зарядился и имеет полярность, указанную на рис. 6. Для упрощения расчетов в момент коммутации конденсатор можно заменить на источник постоянного напряжения или же просто указывать напряжение на конденсаторе. Согласно закону коммутации, напряжение на конденсаторе скачком измениться не может (формула 7):
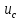 (0-) =
(0-) = 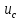 (0+) = 30(B) (7)
(0+) = 30(B) (7)Согласно 2-му закону Кирхгофа для левого контура (формула 8):
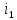 (0+)
(0+)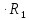 +
+ 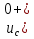 +
+ 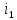 (0+)
(0+)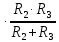 =
=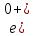 (8)
(8)Отсюда ток источника (формула 9):
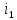 (0+) =
(0+) = 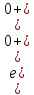 =
= 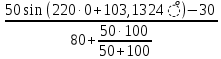 = 0,1649 (A) (9)
= 0,1649 (A) (9)Найдем напряжение на сопротивлении
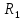 (формула 10):
(формула 10):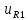 (0+) =
(0+) = 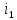 (0+)*
(0+)*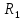 = 0,1649*80 = 13,1946 (B) (10)
= 0,1649*80 = 13,1946 (B) (10)Токи сопротивлений
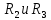 согласно формуле разброса (формулы 11 и 12):
согласно формуле разброса (формулы 11 и 12):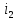 (0+) =
(0+) = 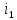 (0+)
(0+)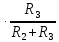 =0,1649
=0,1649 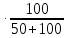 = 0,11 (A) (11)
= 0,11 (A) (11)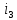 (0+) =
(0+) = 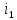 (0+)
(0+)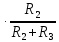 =0,1649
=0,1649 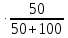 = 0,05498 (A) (12)
= 0,05498 (A) (12)Напряжения сопротивлений
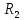 и
и 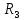
согласно закону Ома
(формула 13):
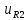 (0+) =
(0+) = 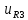 (0+) =
(0+) =  (0+)
(0+)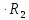 = 0,1
= 0,1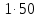 = 5,4978 (B) (13)
= 5,4978 (B) (13)Запишем данные в таблицу 2.
Таблица 2
 (0+), A (0+), A | 0,1649 |
 (0+), B (0+), B | 13,1946 |
 (0+), A (0+), A | 0,11 |
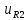 (0+), B (0+), B | 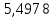 |
 (0+), A (0+), A | 0,05498 |
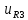 (0+), B (0+), B | 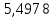 |
 (0+), B (0+), B | 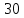 |
Рассчитаем значения в принужденном режиме. Это режим, когда ключ S переключился из положения 1 в положение 2 и прошло бесконечно большое время (рис. 7). Расчет напряжений и токов такой электрической цепи выполняется комплексным методом.
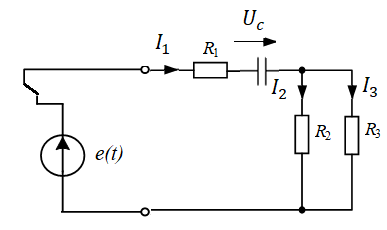
Рис. 7. Электрическая цепь в принужденном режиме
Запишем амплитудное комплексное значение напряжения источника ЭДС (формула 14):
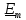 = 50
= 50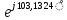 (B) (14)
(B) (14)Найдем значение емкостного сопротивления
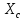 (формула 15):
(формула 15):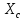 =
=