ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 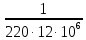 = 378,7879 (Ом) (15)
= 378,7879 (Ом) (15)
Определим эквивалентное сопротивление цепи относительно источника (формула 16):
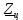 =
= 
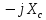 +
+ 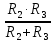 = 80 – j378,7879 +
= 80 – j378,7879 +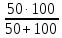 = 113,3333 -378,7879 =
= 113,3333 -378,7879 =
= 395,3792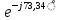 (Ом) (16)
(Ом) (16)
Найдем амплитудное значение комплексного тока источника в цепи по закону Ома (формула 17)
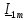 =
= 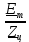 =
= 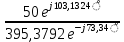 = 0,1265
= 0,1265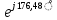 (A) (17)
(A) (17)
Найдем амплитудное комплексное значение напряжения на сопротивлении по закону Ома (формула 18):
по закону Ома (формула 18):
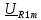 =
= 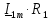 = 0,1265
= 0,1265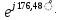 80 =10,1169
80 =10,1169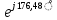 (B) (18)
(B) (18)
Найдем амплитудное комплексное значение напряжение на по закону Ома (формула 19):
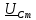 =
=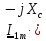 ) = 0,1265
) = 0,1265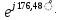 (- j378,7879) = 47,9019
(- j378,7879) = 47,9019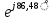 (B) (19)
(B) (19)
Найдем амплитудные значения комплексных токов сопротивлений и
и  согласно формуле разброса (формулы 20 и 21):
согласно формуле разброса (формулы 20 и 21):
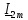 =
=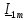
 = 0,1265
= 0,1265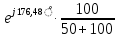 = 0,08431
= 0,08431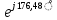
(А) (20)
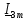 =
=
 = 0,1265
= 0,1265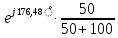 = 0,04215
= 0,04215 (А) (21)
(А) (21)
Найдем амплитудные значения комплексных напряжений сопротивлений и
и  согласно закону Ома (формула 22):
согласно закону Ома (формула 22):
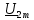 =
= 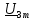 =
= 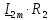 = 0,08431
= 0,08431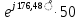 =4,2154
=4,2154 (B) (22)
(B) (22)
Запишем данные в таблицу 6.
Таблица 6
Принужденные значения токов и напряжений
Найдем корни характеристического уравнения. Для этого рассмотрим послекоммутационную схему для свободного режима. В ней все источники ЭДС заменяются на перемычки, источники тока – на разрывы. Индуктивность заменяется на pL , емкость -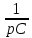 (рис. 8). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 9).
(рис. 8). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 9).
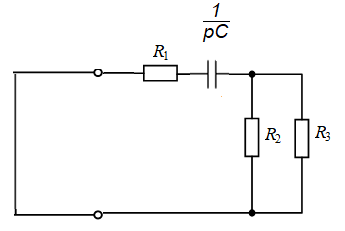
Рис. 10. Электрическая цепь для расчета корней
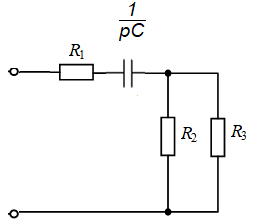
Рис. 11. Электрическая цепь с разрывом для расчета корней
В получившейся электрической цепи операторное сопротивление относительно разрыва (формула 23):
Z(p) = +
+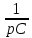
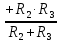 =
= 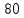 +
+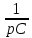
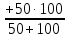 (23)
(23)
Приравняем характеристическое сопротивление к нулю (формула 24) и найдем неизвестный корень p (формула 25):
Z(p) = +
+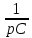
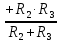 =
= 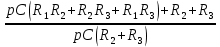 = 0 (24)
= 0 (24)
p = -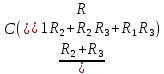 =
= 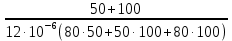 =
=
= -735,2941 (c-1 ) (25)
Корень характеристического уравнения отрицательный, значит переходный процесс закончится.
Постоянная времени цепи (формула 26):
τ =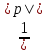 =
= 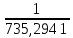 = 1,36
= 1,36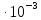 (c) (26)
(c) (26)
Постоянная интегрирования в общем виде рассчитывается (формула 27):
A = a(0+) -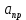
(0+) (27)
Рассчитаем постоянные интегрирования для токов и напряжений
(формулы 28 - 34):
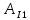 =
=  (0+) -
(0+) -  (0+) = 0,1649- 0,1265sin(
(0+) = 0,1649- 0,1265sin( =0,1572 (A), (28)
=0,1572 (A), (28)
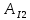 =
=  (0+) -
(0+) -  (0+) = 0,11- 0,08431sin (
(0+) = 0,11- 0,08431sin ( = 0,1048 (A), (29)
= 0,1048 (A), (29)
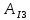 =
=  (0+) -
(0+) -  (0+) = 0,05498- 0,04215sin (
(0+) = 0,05498- 0,04215sin ( = 0,05239 (A), (30)
= 0,05239 (A), (30)
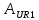 =
=  (0+) -
(0+) -  (0+) = 13,1946– 10,1169sin (
(0+) = 13,1946– 10,1169sin ( =
=
= 12,5726 (B), (31)
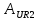 =
=  (0+) -
(0+) -  (0+) =
(0+) =  - 4,2154sin(
- 4,2154sin( =
=
= 5,2386 (B), (32)
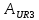 =
=  (0+) -
(0+) -  (0+) =
(0+) =  - 4,2154sin(
- 4,2154sin( =
=
= 5,2386 (B), (33)
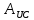 =
=  (0+) -
(0+) -  (0+) =
(0+) =  -
- 
( =
=
= -17,8112 (B), (34)
Запишем значения свободных составляющих (формулы 35–41):
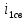 (t) =
(t) = 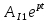 = 0,1572
= 0,1572 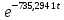 (A) , (35)
(A) , (35)
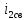 (t) =
(t) = 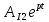 = 0,1048
= 0,1048 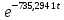 (A) , (36)
(A) , (36)
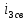 (t) =
(t) = 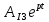 = 0,05239
= 0,05239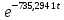 (A), (37)
(A), (37)
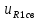 (t) =
(t) = 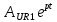 = 12,5726
= 12,5726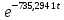 (B), (38)
(B), (38)
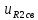 (t) =
(t) = 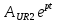 = 5,2386
= 5,2386 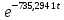 B), (39)
B), (39)
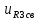 (t) =
(t) = 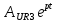 = 5,2386
= 5,2386 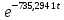 (B), (40)
(B), (40)
 (t) =
(t) = 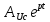 = -17,8112
= -17,8112 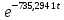 (B). (41)
(B). (41)
Запишем зависимость изменения напряжений и токов от времени при переходном процессе как сумму свободной и принужденной составляющей с учетом значений до коммутации (формулы 42-48):

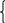 (t) =
(t) = 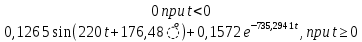 (A), (42)
(A), (42)

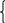 (t) =
(t) = 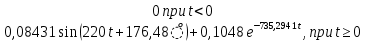 (A), (43)
(A), (43)

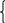
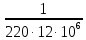 = 378,7879 (Ом) (15)
= 378,7879 (Ом) (15)Определим эквивалентное сопротивление цепи относительно источника (формула 16):
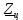 =
= 
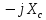 +
+ 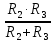 = 80 – j378,7879 +
= 80 – j378,7879 +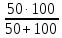 = 113,3333 -378,7879 =
= 113,3333 -378,7879 == 395,3792
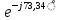 (Ом) (16)
(Ом) (16)Найдем амплитудное значение комплексного тока источника в цепи по закону Ома (формула 17)
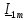 =
= 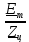 =
= 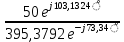 = 0,1265
= 0,1265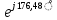 (A) (17)
(A) (17)Найдем амплитудное комплексное значение напряжения на сопротивлении
 по закону Ома (формула 18):
по закону Ома (формула 18):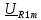 =
= 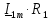 = 0,1265
= 0,1265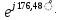 80 =10,1169
80 =10,1169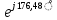 (B) (18)
(B) (18)Найдем амплитудное комплексное значение напряжение на по закону Ома (формула 19):
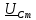 =
=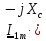 ) = 0,1265
) = 0,1265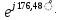 (- j378,7879) = 47,9019
(- j378,7879) = 47,9019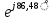 (B) (19)
(B) (19)Найдем амплитудные значения комплексных токов сопротивлений
 и
и  согласно формуле разброса (формулы 20 и 21):
согласно формуле разброса (формулы 20 и 21): 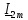 =
=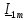
 = 0,1265
= 0,1265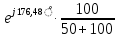 = 0,08431
= 0,08431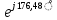
(А) (20)
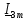 =
=
 = 0,1265
= 0,1265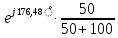 = 0,04215
= 0,04215 (А) (21)
(А) (21)Найдем амплитудные значения комплексных напряжений сопротивлений
 и
и  согласно закону Ома (формула 22):
согласно закону Ома (формула 22): 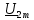 =
= 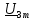 =
= 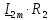 = 0,08431
= 0,08431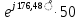 =4,2154
=4,2154 (B) (22)
(B) (22)Запишем данные в таблицу 6.
Таблица 6
Принужденные значения токов и напряжений
| Комплексные значения в принужденном режиме | |
 , A , A | 0,1265  |
 , B , B | 10,1169  |
 , A , A | 0,08431  |
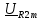 , B , B | 4,2154  |
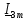 , A , A | 0,04215  |
 ,B ,B | 4,2154  |
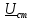 , B , B | 47,9019  |
| Принужденные мгновенные значения | |
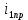 (t) , A (t) , A | 0,1265sin(220t+ 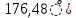 |
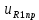 (t), B (t), B | 10,1169sin(220t+ 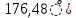 |
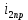 (t) , A (t) , A | 0,08431sin(220t+ 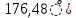 |
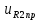 (t), B (t), B | 4,2154sin(220t+ 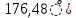 |
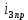 (t) , A (t) , A | 0,04215sin(220t+ 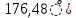 |
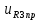 (t), B (t), B | 4,2154sin(220t+ 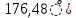 |
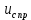 (t), B (t), B | 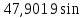 (220t+ (220t+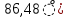 |
Найдем корни характеристического уравнения. Для этого рассмотрим послекоммутационную схему для свободного режима. В ней все источники ЭДС заменяются на перемычки, источники тока – на разрывы. Индуктивность заменяется на pL , емкость -
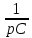 (рис. 8). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 9).
(рис. 8). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 9).
Рис. 10. Электрическая цепь для расчета корней

Рис. 11. Электрическая цепь с разрывом для расчета корней
В получившейся электрической цепи операторное сопротивление относительно разрыва (формула 23):
Z(p) =
 +
+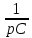
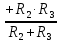 =
= 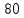 +
+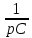
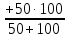 (23)
(23)Приравняем характеристическое сопротивление к нулю (формула 24) и найдем неизвестный корень p (формула 25):
Z(p) =
 +
+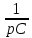
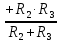 =
= 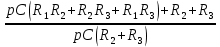 = 0 (24)
= 0 (24)p = -
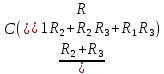 =
= 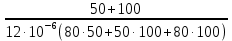 =
== -735,2941 (c-1 ) (25)
Корень характеристического уравнения отрицательный, значит переходный процесс закончится.
Постоянная времени цепи (формула 26):
τ =
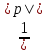 =
= 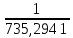 = 1,36
= 1,36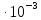 (c) (26)
(c) (26)Постоянная интегрирования в общем виде рассчитывается (формула 27):
A = a(0+) -
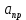
(0+) (27)
Рассчитаем постоянные интегрирования для токов и напряжений
(формулы 28 - 34):
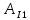 =
=  (0+) -
(0+) -  (0+) = 0,1649- 0,1265sin(
(0+) = 0,1649- 0,1265sin( =0,1572 (A), (28)
=0,1572 (A), (28)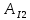 =
=  (0+) -
(0+) -  (0+) = 0,11- 0,08431sin (
(0+) = 0,11- 0,08431sin ( = 0,1048 (A), (29)
= 0,1048 (A), (29)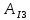 =
=  (0+) -
(0+) -  (0+) = 0,05498- 0,04215sin (
(0+) = 0,05498- 0,04215sin ( = 0,05239 (A), (30)
= 0,05239 (A), (30)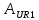 =
=  (0+) -
(0+) -  (0+) = 13,1946– 10,1169sin (
(0+) = 13,1946– 10,1169sin ( =
== 12,5726 (B), (31)
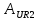 =
=  (0+) -
(0+) -  (0+) =
(0+) =  - 4,2154sin(
- 4,2154sin( =
== 5,2386 (B), (32)
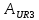 =
=  (0+) -
(0+) -  (0+) =
(0+) =  - 4,2154sin(
- 4,2154sin( =
== 5,2386 (B), (33)
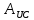 =
=  (0+) -
(0+) -  (0+) =
(0+) =  -
- 
(
 =
== -17,8112 (B), (34)
Запишем значения свободных составляющих (формулы 35–41):
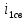 (t) =
(t) = 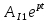 = 0,1572
= 0,1572 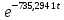 (A) , (35)
(A) , (35)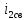 (t) =
(t) = 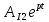 = 0,1048
= 0,1048 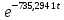 (A) , (36)
(A) , (36)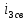 (t) =
(t) = 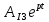 = 0,05239
= 0,05239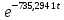 (A), (37)
(A), (37)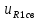 (t) =
(t) = 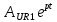 = 12,5726
= 12,5726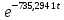 (B), (38)
(B), (38)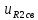 (t) =
(t) = 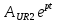 = 5,2386
= 5,2386 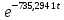 B), (39)
B), (39)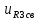 (t) =
(t) = 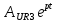 = 5,2386
= 5,2386 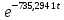 (B), (40)
(B), (40) (t) =
(t) = 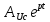 = -17,8112
= -17,8112 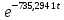 (B). (41)
(B). (41)Запишем зависимость изменения напряжений и токов от времени при переходном процессе как сумму свободной и принужденной составляющей с учетом значений до коммутации (формулы 42-48):

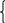 (t) =
(t) = 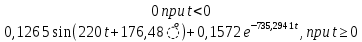 (A), (42)
(A), (42)
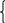 (t) =
(t) = 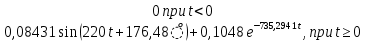 (A), (43)
(A), (43)