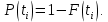Файл: Пояснительная записка к расчетнографической работе по дисциплине Надежность и диагностика технологических систем.docx

МИНИСТЕРСТВО НАУКИ И высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»Кафедра проектирования технологических машинПояснительная записка к расчетно-графической работе по дисциплине: Надежность и диагностика технологических системВариант 13Выполнил: Юлусов И.С. (ФИО и подпись студента)Группа Маг - 721Механико- технологический факультет (факультет)Направление 15.03.04 – Конструкторско-технологическое(код и наименование )обеспечение машиностроительных производствРуководитель Зверев Е. А.(подпись, инициалы, фамилия) Новосибирск 2022 г.

Содержание

Цель работы: определение гамма-процентного ресурса технологического оборудования, оснастки или режущего инструмента при заданных условиях эксплуатации.По результатам производственных испытаний 40 фрез были установлены следующие значения наработки до отказа режущих инструментов (мин) (таблица 1)Таблица 1 – Исходные данные

931	538	1731	497	584	826	1539	1360	688	1080
689	876	1261	1151	866	761	1113	1097	879	815
219	1925	939	855	857	963	1177	1217	231	1882
476	836	728	1041	893	954	645	484	640	2075

---

1 Построение вариационного ряда

Начальная расстановка значений случайной величины в порядке возрастания необходима для удобства выполнения расчетов: 219, 231, 476, 484, 497, 538, 584, 640, 645, 688, 689, 728, 761, 815, 826, 836, 855, 857, 866, 876, 879, 893, 931, 939, 954, 963, 1041, 1080, 1097, 1113, 1151, 1177, 1217, 1261, 1360, 1539, 1731, 1882, 1925, 2075.Построение интервального вариационного ряда осуществляется в определенном порядке: а) находятся границы рассеивания, т. е. наибольшее 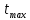и наименьшее 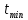значения. 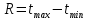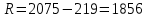Разность между ними является размахом варьирования:Далее устанавливается количество интервалов к, на которое необходимо разбить размах R. 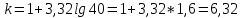Число k должно быть не менее k =1+3,32lgN, где N - объем выборки испытаний.Принимаем числа k = 7.Находится ширина интервала вариационного ряда:Находится ширина интервала вариационного ряда:

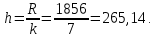
2 Построение интервального вариационного ряда:

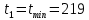
Определяются границы интервалов, для чего вначале устанавливается нулевое (крайнее) значение интервала: Следующие границы интервалов рассчитываются последовательным прибавлением ширины интервала h к предыдущему значению, т.е.

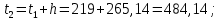
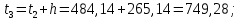
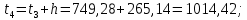
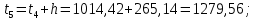
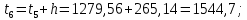
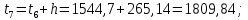
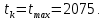
3 Группировка результатов наблюдений

Для группирования результатов наблюдений в каждый интервал включаются данные, большие нижней границы интервала или равные ей и меньшие верхней границы. По каждому интервалу подсчитывается середина интервала:

---

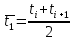
Определяется частота попадания 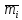(опытная частота) t в i-й интервал, все результаты предоставляются в виде таблицы 2.Таблица 2 – Частота попадания в интервал

Номер интервала	Границы интервалов	Середины интервалов	Частота попада­ния в интервал
1-й		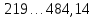351,57	3
2-й		616,71	9
3-й		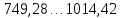881,85	14
4-й		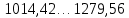1146,99	7
5-й		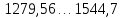1412,13	3
6-й		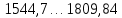1677,27	1
7-й		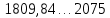1942,41	3

4 Определение параметров и характеристик закона распределения

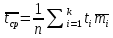
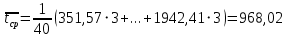
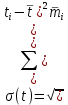
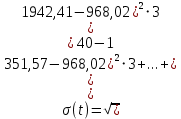
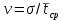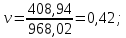
Основные параметры закона распределения определяются на базе ранее рассмотренных формулСреднее арифметическое наработки:Вычисляем среднее квадратическое отклонение наработки:Значение коэффициента вариации: ;Строим гистограмму распределения частоты отказов фрез по наработке

---

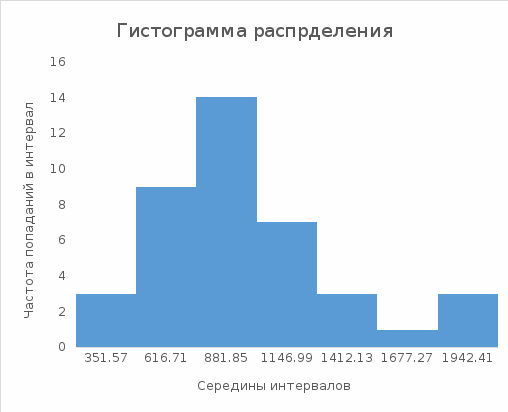
t (рисунок 1).Рисунок 1 - Гистограмма распределения отказов инструментов по наработкеПо виду гистограммы и значению коэффициента вариации  = 0,42 предполагаем, что отказы инструментов согласуются с законом Вейбулла.Необходимо проверить полученный ряд на выпадающие (ошибочные) точки, не соответствующие закону распределения. Приближенную проверку проводят по правилу 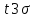следующим образом. От полученного среднего значения t последовательно вычитают и прибавляют величину 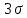. Если крайние точки ряда не выходят за пределы, то все точки ряда считаются действительными. В противном случае исключают подозрительные точки и корректируют результаты расчетов.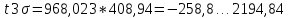 Можно сделать вывод, что все значения укладываются в трехсигмовый диапазон.

5 Определение закона распределения

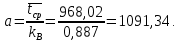
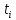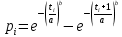
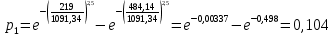
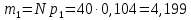
Согласно таблице приложения 3 [1] определяем значения параметров распределения Вейбулла для рассчитанного коэффициента вариации:b = 2,5; k_B = 0,887; q_B= 0,380.Определяем второй параметр распределения:Вычисляем теоретические вероятности попадания случайной величины в интервалы наработки:Для остальных интервалов найденные значения сводим в таблицу 3.Таблица 3 – Результаты расчетов

Характеристика	Интервал
	1-й	2-й	3-й	4-й	5-й	6-й	7-й
Теоретическая вероятность pi	0,104	0,200	0,241	0,209	0,133	0,063	0,022
Теоретическая частота mi	4,199	8,019	9,678	8,361	5,339	2,531	0,885

---

Для остальных интервалов расчетные значения m_i сведём в таблицу 4Таблица 4 – Результаты расчетов

i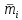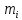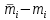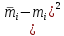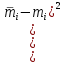
1	3	4,199	-1,199	1,437601	0,342367
2	9	8,019	0,981	0,962361	0,12001
3	14	9,678	4,322	18,67968	1,930118
4	7	8,361	-1,361	1,852321	0,221543
5	3	5,339	-2,339	5,470921	1,024709
6	1	2,531	-1,531	2,343961	0,926101
7	3	0,885	2,115	4,473225	5,054492
∑	40				Х 2опыт = 9,41934

Значений критерия Пирсона при уровне значимости α = 0,05 и числе степеней свободы S = k - r - 1=7-2-1=4 находим 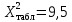. Так как 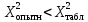, гипотеза о распределении наработок по закону Вейбулла не отвергается.Для построения кривых вероятностей отказа F(t) и вероятности безотказной работы P(t) воспользуемся формулами:

---