Файл: Решение Выполним замену Выполним замену переменной.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 33

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Министерство науки и высшего образования Российской Федерации

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕСИТЕТ (НИУ МГСУ)

Кафедра высшей математики

Контрольные задания компьютерных практикумов

Вариант № 9

Выполнил

Группа 2022-58-б

№ зачетной книжки 22-Б-02327

Проверил Макаров В.И.

Москва 2023г.

Задание №1

Найти неопределенные интегралы:







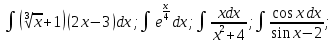
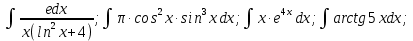
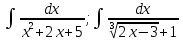
Решение:











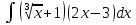
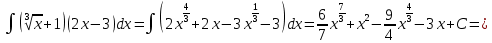
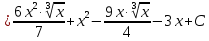
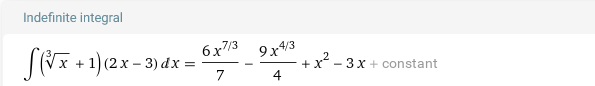
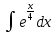
Выполним замену:









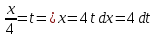
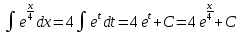
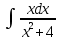
Выполним замену переменной:









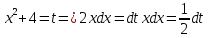
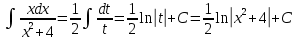
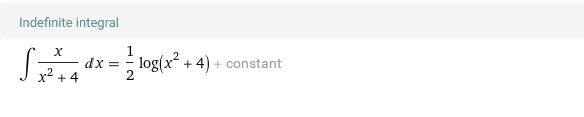
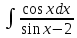
Выполним замену переменной:









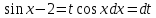
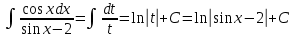
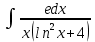
Выполним замену переменной:













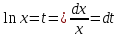
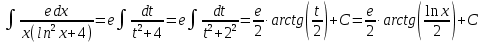
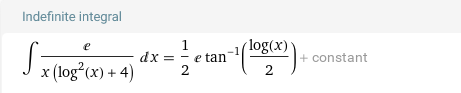
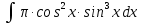
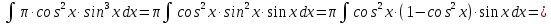
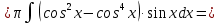
Выполним замену:













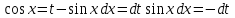
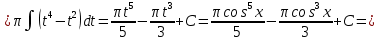
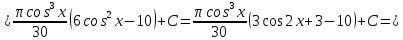
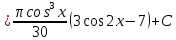
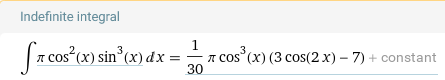
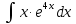
Применим формулу интегрирования по частям:











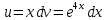
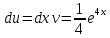
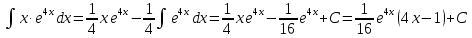
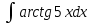
Применим формулу интегрирования по частям:







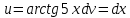
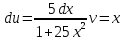
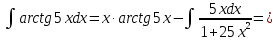
Выполним замену:













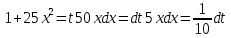
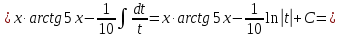
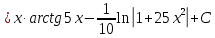
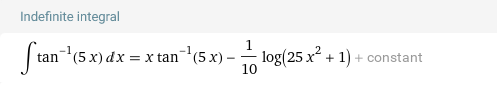
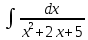
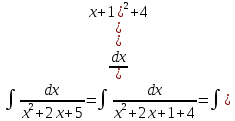
Выполним замену:









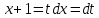
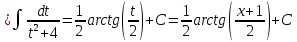
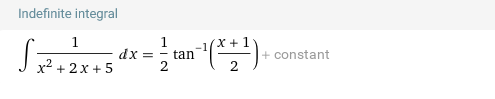
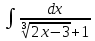
Выполним замену:





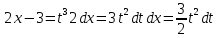
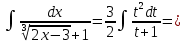
Разделим числитель на знаменатель:
















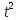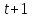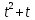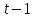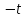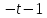1









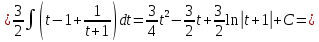
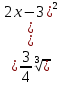
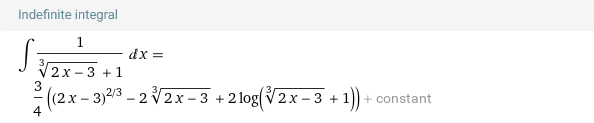
Задание №2

  1. Вычислить площадь фигуры, ограниченной линиями:



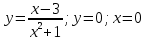
  1. Найти длину участка кривой:



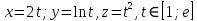
  1. Найти площадь поверхности, образованной вращением кривой , вокруг оси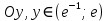

Решение:

  1. Площадь фигуры найдем с помощью определенного интеграла:













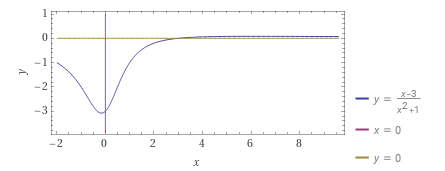
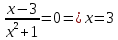
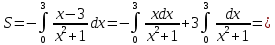
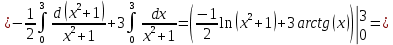
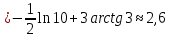
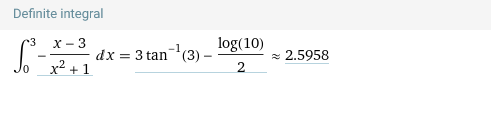
  1. Длину дуги, заданной параметрическими уравнениями, найдем по формуле:















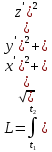
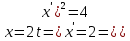
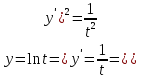
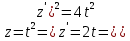
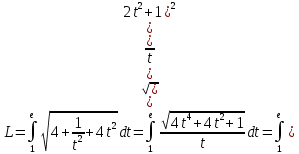
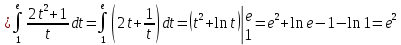
  1. Площадь поверхности вращения фигуры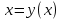 вокруг оси 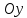найдем по формуле:















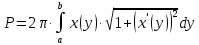
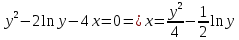
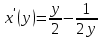
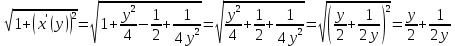
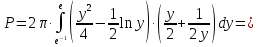
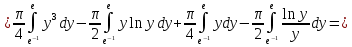
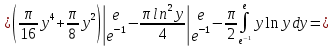
Применим формулу интегрирования по частям:













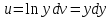
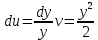
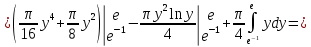
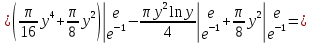
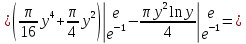
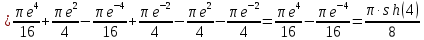
Задание №3

1) - 4) Найти общее решение линейного однородного дифференциального уравнения.









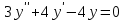
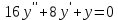
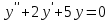
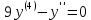
5) Написать вид общего решения.



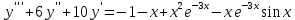
6) Решить задачу Коши для линейного неоднородного дифференциального уравнения.




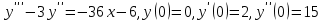
7) – 9) Найти общее решение линейного неоднородного дифференциального уравнения.







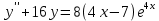
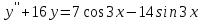
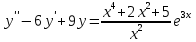
Решение:



Составим характеристическое уравнение:





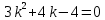
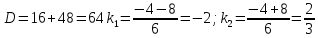
Корни характеристического уравнения действительные различные, поэтому:







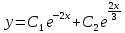
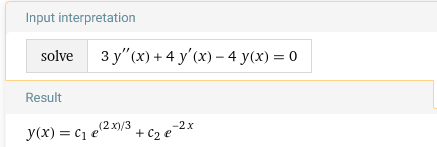
Составим характеристическое уравнение:





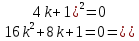
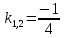
Корни характеристического уравнения действительные кратные, поэтому:







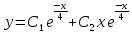
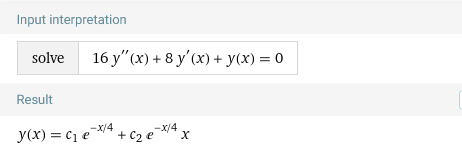
Составим характеристическое уравнение:







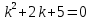
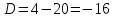
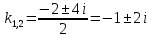
Корни характеристического уравнения комплексные сопряженные, поэтому:







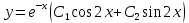
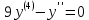
Составим характеристическое уравнение:







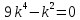
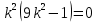
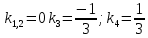
Корни действительные, есть кратные и есть различные, поэтому решение:

Смотрите также файлы