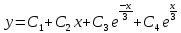
Найдем общее решение однородного уравнения:



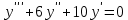
Характеристическое уравнение:









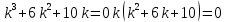
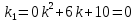
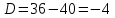
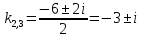
Корни действительные и комплексные сопряженные, поэтому общее решение однородного уравнения:



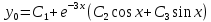
Правая часть уравнения является суммой функций специального вида. Найдем частное решение для каждой из функций:











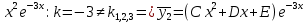
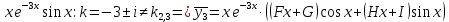
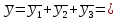
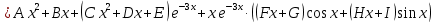
Общий вид решения:







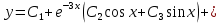
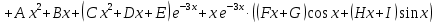
Найдем общее решение однородного уравнения:



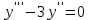
Характеристическое уравнение:







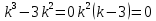
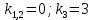
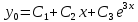
Найдем частное решение неоднородного уравнения. Правая часть уравнения является функцией специального вида с характеристическим числом 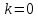, совпадающее с корнем характеристического уравнения кратности 2, поэтому частное решение будем искать в виде: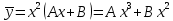

---

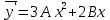
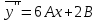
Подставим в исходное уравнение:









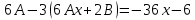
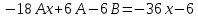
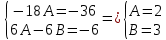
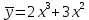
Общее решение уравнения:



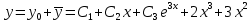
Найдем частное решение, удовлетворяющее начальным условиям:













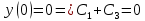
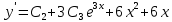
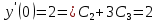
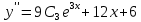
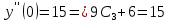
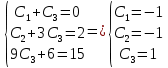
Частное решение уравнения:







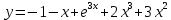
Найдем общее решение однородного уравнения:



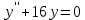
Характеристическое уравнение:



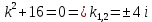
Корни характеристического уравнения комплексные сопряженные, поэтому общее решение однородного уравнения:



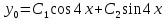
Правая часть является функцией специального вида с характеристическим числом 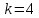, не совпадающим с корнем характеристического уравнения, поэтому частное решение будем искать в виде: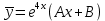







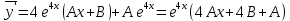
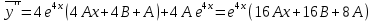
Подставим данные значения в исходное уравнение:

---

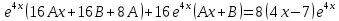
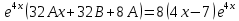
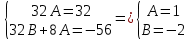
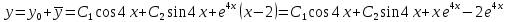
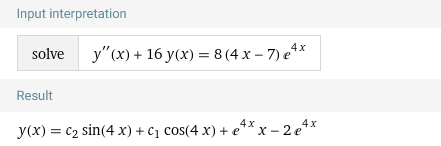
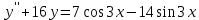
Найдем общее решение однородного уравнения:



Характеристическое уравнение:



Корни характеристического уравнения комплексные сопряженные, поэтому общее решение однородного уравнения:



Правая часть является функцией специального вида с характеристическим числом 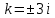, не совпадающим с корнем характеристического уравнения, поэтому частное решение будем искать в виде: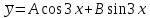







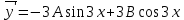
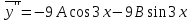
Подставим данные значения в исходное уравнение:









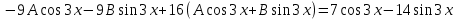
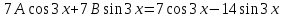
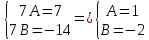
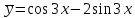
Общее решение уравнения:







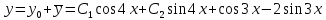
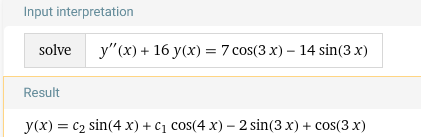
Найдем общее решение однородного уравнения:



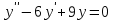
Составим и решим характеристическое уравнение:



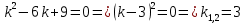
Корни характеристического уравнения действительные кратные, поэтому общее решение однородного уравнения:



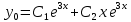
Общее решение неоднородного уравнения будем искать в виде:



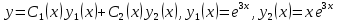
Неизвестные функции

---

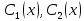найдем из системы уравнений: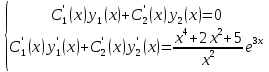







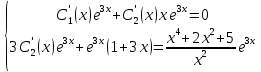
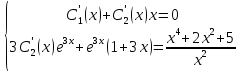
Решим по формулам Крамера:

















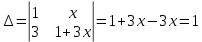
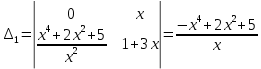
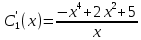
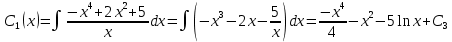
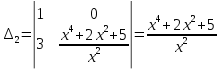
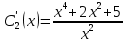
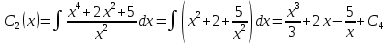
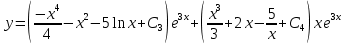
Задание №4

В лифт пятиэтажного дома на первом этаже вошли три человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Дискретная случайная величина – число человек, выходящих на четвертом этаже. Найти: ряд распределения, числовые характеристики, функцию распределения 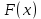. Построить график .

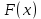Решение:

Проводится серия повторных независимых испытаний проверки человека.

Число испытаний

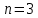
Пусть событие 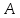– человек вышел на четвертом этаже. Так как каждый может выйти на любом из четырех этажей, то: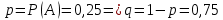



Вероятность того, что в 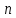независимых повторных испытаниях событие 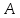наступит ровно 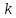раз, найдем по формуле Бернулли: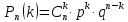

---

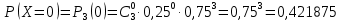
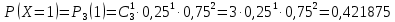
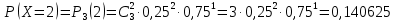
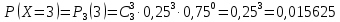
Ряд распределения:

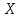	0	1	2	3
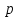	0,421875	0,421875	0,140625	0,015625

Числовые характеристики биномиального распределения:







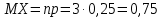
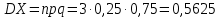
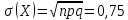
Функцию распределения запишем по формуле:















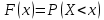
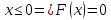
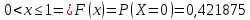
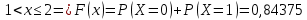
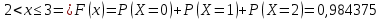
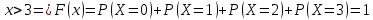
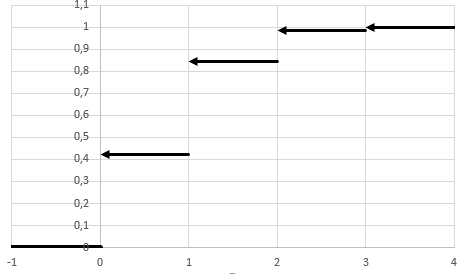
Задание №5

Результаты гидрологических наблюдений в течение 20 лет за величиной годового стока реки (в кубических километрах) приведены ниже:

0,82	0,79	0,85	0,81	0,82
0,81	0,82	0,85	0,81	0,81
0,8	0,79	0,8	0,83	0,79
0,76	0,79	0,74	0,8	0,81

Найти доверительные интервалы для среднего значения годового стока с надежностью 0,9 и среднеквадратического отклонения от среднего значения с надежностью 0,95. Принять, что определяемая величина распределена по нормальному закону.

Решение:

Составим вариационный статистический ряд:

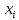	0,74	0,76	0,79	0,8	0,81	0,82	0,83	0,85
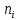	1	1	4	3	5	3	1	2

---

Смотрите также файлы

• Телевидение и литература что окажется сильнее.docx

• Методические рекомендации по организации и прохождению учебной практики.doc

• Информация о разработчике плана.docx

• Программа производственной практики практики по получению профессиональных умений и опыта.docx

• Контрольная работа Экономика.docx