ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности
| (наименование института полностью) |
| 20.03.01 Техносферная безопасность |
| (код и наименование направления подготовки / специальности) |
| Противопожарные системы |
| (направленность (профиль) / специализация) |
ПрактическОе заданиЕ 8,9
по учебному курсу «Механика»
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задание 8
Дано:
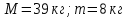
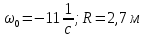
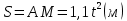
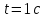
Найти:
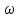
Решение
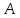
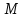
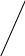
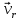
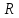
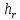
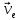
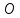
Рис. 1
Применим теорему об изменении кинетического момента системы относительно оси
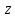(ось направлена перпендикулярно плоскости чертежа и проходит через точку ):
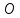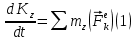
На систему действуют внешние силы: силы тяжести
, 
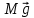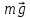, параллельные оси 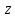, и реакция 
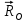неподвижной шарнирной опоры 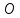. Моменты сил 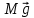, , 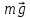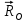относительно оси 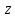равны нулю (силы ,
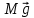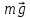
параллельны оси
, а сила 
пересекает эту ось). Следовательно, уравнение (1) примет вид: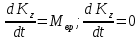
Отсюда
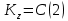
Кинетический момент системы при вращении пластины не меняется.
Составим кинетический момент рассматриваемой системы относительно оси
:
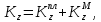(3)где
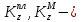кинетические моменты пластины и точки 
соответственно.Так как пластина вращается вокруг оси
, то кинетический момент пластины равен: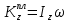
Момент инерции пластины относительно оси вращения находим по теореме Штейнера:
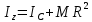
Момент инерции круглой пластины относительно вертикальной оси, проходящей через центр тяжести, определяем по формуле:
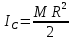
Тогда
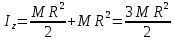
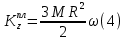
Определим
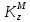. Движение точки рассмотрим как сложное, считая её движение вдоль канала относительным, а вращение пластины переносным движением. Тогда абсолютная скорость точки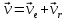
Используя теорему Вариньона, найдём кинетический момент точки
относительно оси :
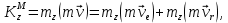
где
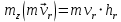
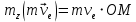
Относительная скорость:
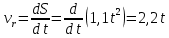
Переносная скорость:
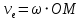
Таким образом, получаем:
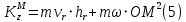
Величина
есть плечо, то есть длина перпендикуляра, опущенного из точки 
на линию действия вектора 
. Из геометрических соображений (рис. 1) определяем: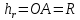
Расстояние
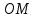точки от оси вращения определяем из прямоугольного треугольника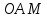 
(рис. 1):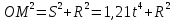
Подставив все данные в выражение (5), получим:
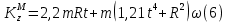
Подставим (4) и (6) в (3):
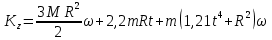
Или
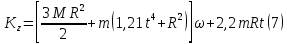
Подставив (7) в (2), получим:
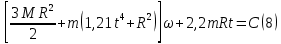
Подставим числовые данные:
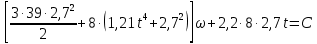
Или
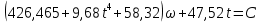
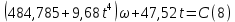
Постоянную
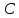определим по начальному условию: 
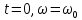, откуда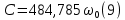
Из (8) и (9) получаем зависимость угловой скорости пластины от времени:
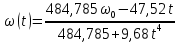
Вычисляем значение угловой скорости в заданный момент времени
:
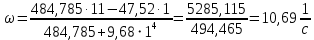
Ответ:
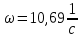
Задание 9
Дано:
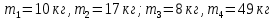
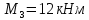
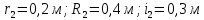
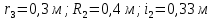
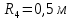
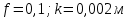
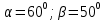
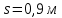
Найти:
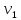в момент, когда 
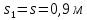.Решение
2 
3
1 
