ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
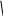
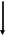
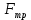
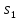
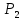
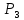
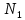
4 
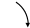
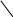
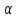
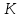
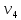
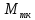
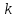
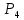
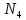
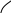
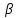
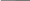
Рис. 1
Применим теорему об изменении кинетической энергии системы:
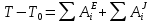
Так как система состоит из абсолютно твёрдых тел, соединённых нерастяжимыми нитями, то сумма работ внутренних сил системы равна нулю:
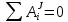. В начальном положении система находится в покое, следовательно, 
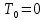. Тогда уравнение примет вид: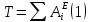
Кинетическая энергия системы в конечном положении равна сумме кинетических энергий всех тел системы:
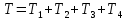(2)Кинетическая энергия груза 1, движущегося поступательно:
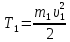
Кинетическая энергия тел 2 и 3, вращающихся вокруг неподвижных осей:
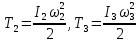
Кинетическая энергия катка 4, совершающего плоскопараллельное движение:
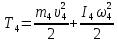
Моменты инерции тел равны:
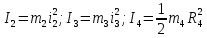
Подставив все данные в формулу (2), получим:
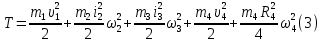
Выразим входящие сюда скорости
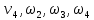через скорость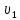 
груза 1.
Из рис. 1 определяем:
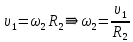
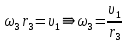
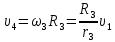
Точка
является мгновенным центром скоростей катка 4, следовательно,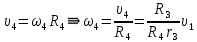
Подставим полученные выражения скоростей в равенство (3):
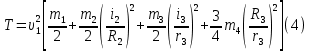
Находим сумму работ всех внешних сил, приложенных к системе, на заданном перемещении груза 1.
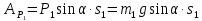
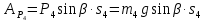
Работа силы трения скольжения груза 1:
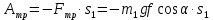
Работа движущего момента шкива 3:
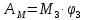
Работа пары сил трения качения катка 4:
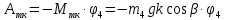
где
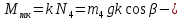момент силы сопротивления трения качения. Выразим перемещения 
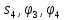через заданное перемещение 
груза 1. При этом учтём, что зависимость между перемещениями такая же, как и между соответствующими скоростями: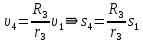
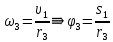
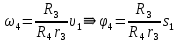
Подставим найденные перемещения в выражения работ и определим их сумму:
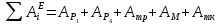
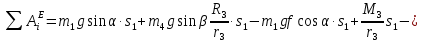
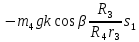
Или
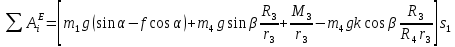
По теореме (1) приравняем значения
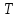и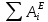 
:
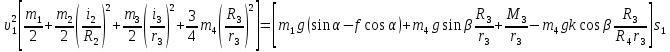
Отсюда определяем скорость груза 1:
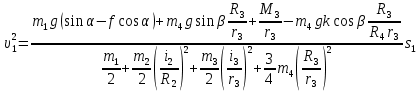
Вычислим отдельно числитель и знаменатель полученного выражения:
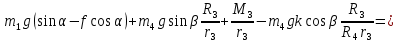
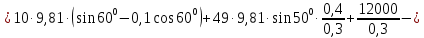
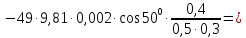
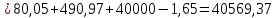
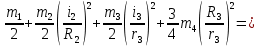
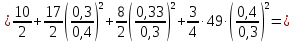
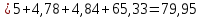
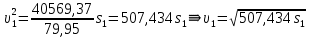
При заданном значении
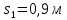получаем: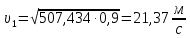
Ответ:
