Задача 1. Сколькими способами можно выбрать 2 детали из ящика, содержащего 7 деталей, имеющих круглое и квадратное сечения?

, где факториал K!=1·2·3·...·(K–1)·K.



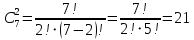
Задача 2. На карточках написаны буквы, образующие слово «ВЕРТОЛЁТ». Карточки перемешивают и из них наугад последовательно извлекают и выкладывают слева направо четыре карточки. Найдем вероятность того, что получится слово «ЛЕТО» (событие A).

Слово «ВЕРТОЛЕТ» состоит из 8 букв. Вероятность того, что будет извлечена карточка с буквой Л, равна 1/8. Условная вероятность, что будет извлечена карточка Е, если первой извлечена Л, равна 1/7. Условная вероятность, что будет извлечена карточка Т, если первой извлечена Л и Е равна 2/6. Условная вероятность, что будет извлечена карточка О, если первой извлечена Л, Е и Т равна 1/5. Тогда вероятность произведения событий «Л», «Е», «Т», «О» равна (1/8)∙(1/7)∙(2/6) )∙(1/5)=1/840=0.0011904761904762

Задача 3. Имеются 2 барабана, в которых находятся выигрышные билеты. В первом барабане из 200 билетов выигрышных 6. Во втором барабане из 250 билетов выигрышных 10. Из каждого ящика на удачу вынимается по одному билету. Найти вероятность того, что оба билета окажутся выигрышными. Найти вероятность того, что оба билета окажутся невыигрышными.

Всего невыигрышных билетов: 450-16 = 434

Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 2 билета из 450:



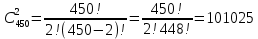
2. Найдем вероятность того, что все выбранные билеты - выигрышные.

---

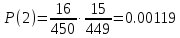
3. Найдем вероятность того, что все выбранные билеты - невыигрышные.



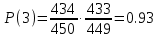
Задача 4. Завод отправил на базу 10 000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, составляет р=0,0001. Найти вероятность того, что на базу прибудут ровно 2 поврежденных изделия.

Вероятность р мала, а число n велико (np = 1 < 10). Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон распределения.

Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле:
Найдем ряд распределения X.

Здесь λ = np = 10000*0.0001 = 1

P(0) = e^{- λ} = e^-1 = 0.3679

P(1) = λ*e^-λ = 1e^-1 = 0.3679
Ответ: 0.3679, 0.3679, 0.1839

Задача 5. Случайная величина Х распределена по нормальному закону. Математическое ожидание равно 30, среднее квадратическое отклонение равно 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу [12, 20].

Вероятность попадания величины X в заданный интервал (α ; β).

где Ф(x) — функция Лапласа
Учитывая, что функция Лапласа нечетная, т.е. Ф(-x) = -Ф(x), получим:


Задача 6. В ящике 40 деталей, из которых 15 стандартных. Из ящика наугад взяли 6 деталей. Найти вероятность того, что среди наугад взятых 6 деталей хотя бы одна стандартная.

Всего нестандартных деталей: 45-15 = 30

Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 6 деталей из 45:
1. Найдем вероятность того, что среди выбранных 6 деталей один стандартный.

Подсчитаем число исходов, благоприятствующих данному событию:

а) одину деталь среди 15 стандартных можно выбрать способами, количество которых равно:
б) Остальные 5 нестандартных можно выбрать из 30 белых:

1. Найдем вероятность того, что среди выбранных 6 деталей 1 стандартная.
Количество вариантов выбора из 15 стандартных деталей:
Количество вариантов выбора из 30 нестандартных деталей остальные 5 стандартные:
Ответ: 0.262

Задача 7. Смешанная СВ задана следующим образом:

• 
  рядом распределения:
  

  X	3	6	9
  P	0,95	0,02	0,03

• 
  плотностью распределения вероятностей:
  

---

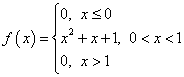
Найти математическое ожидание.

Функция распределения.

F(x)=∫-∞xf(x)·dx

F(x)=∫∞00·dx=0, x ≤0

F(x)=∫0x(x²+x+1)·dx= ,0< x ≤1

F(x)=1, x >1


Математическое ожидание.

M(x)=∫abx·f(x)·dx


Найдем интеграл:

∫x·(x²+x+1)·dx


Представим исходный интеграл, как сумму интегралов:

∫x·(x²+x+1)·dx=∫x³·dx+∫x²·dx+∫x·dx


a)∫nan·dx


b)∫x²·dx


Это табличный интеграл:

c)∫x·dx


Это табличный интеграл:

Вычислим определенный интеграл:

∫()((01x·(x²+x+1)·dx)= =1.083333333333333


Дисперсия.

D(x)=∫abx²·f(x)·dx-M(x)²


Найдем интеграл:

∫x²·(x²+x+1)·dx


Представим исходный интеграл, как сумму интегралов:

∫x²·(x²+x+1)·dx=∫x⁴·dx+∫x³·dx+∫x²·dx


a)∫nan·dx


b)∫x³·dx


Это табличный интеграл:

c)∫x²·dx


Это табличный интеграл:

---

Вычислим определенный интеграл:

∫()((01x²·(x²+x+1)·dx)= =0.7833333333333333

D(x)= =

Задача 8. Найти дисперсию непрерывной СВ Х, если задана плотность распределения:



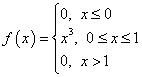
Функция распределения.

F(x)=∫-∞xf(x)·dx

F(x)=∫∞00·dx=0, x ≤0

F(x)=∫0xx³·dx= ,0< x ≤1

F(x)=1, x >1


Математическое ожидание.

M(x)=∫abx·f(x)·dx


Найдем интеграл:

∫x·x³·dx

∫nan·dx


Вычислим определенный интеграл:

∫()((01x·x³·dx)= =0.2


Дисперсия.

D(x)=∫abx²·f(x)·dx-M(x)²


Найдем интеграл:

∫x²·x³·dx

∫nan·dx


Вычислим определенный интеграл:

∫()((01x²·x³·dx)= =0.1666666666666667


D(x)= =
Среднеквадратическое отклонение.

s= = =

---

Задача 9. Двумерная случайная величина задана плотностью совместного распределения: f(x,y) = 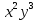 на участке от 0 до 1 и f(x,y)=0 вне этого участка. Определить, зависимы или нет составляющие случайные величины.

Если для всех значений (x,y) выполняется равенство f(x,y)= f(x) f(y), тослучайные величины x,y называются независимыми.



Найдем одномерные плотности для X и Y по формулам:

,





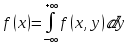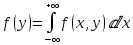
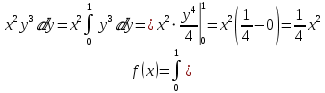
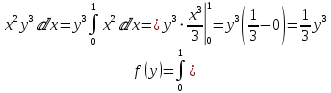
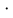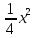
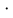
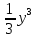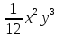
Так как f(x) f(y) = = 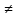f(x,y) = 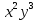, то величины X и Y зависимы.

Задача 10. Задана плотность совместного распределения двумерной случайной величины f(x,y)= C* 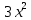*2y в квадрате 0≤X<1, 0≤Y<1. Вне этого квадрата f(x,y)=0. Найти параметр С.



Найдем параметр C из условия нормировки





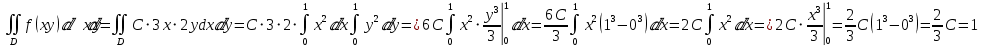
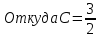
Ответ:

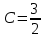
Задача 11. Задано распределение частот выборки:

xi	13	17	19
ni	22	28	35

---

Смотрите также файлы

• Задача Задание.docx

• 1. Структура и история ао "ArcelorMittal".docx

• Реферат по теме языковые нормы русской речи.docx

• Тема. Понятие о сложноподчиненном предложении.docx

• Тушение пожаров в условиях особой опасности для личного состава подразделений пожарной охраны.docx