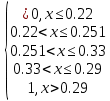Файл: Задача Сколькими способами можно выбрать 2 детали из ящика, содержащего 7 деталей, имеющих круглое и квадратное сечения.docx
Добавлен: 25.10.2023
Просмотров: 158
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построить эмпирическую функцию распределения.
Вычислим объем выборки: n=22+28+35=85
Наименьшая варианта равна: x1=13, поэтому F*(x)=0 при x≤13
Значения X<17, а именно: x1=13, наблюдались 22 раз, следовательно, F*(x)=22/85= при 13< x≤17
Значения X<19, а именно: x1=13, x2=17, наблюдались 50 раз, следовательно, F*(x)=50/85= при 17< x≤19
Т.к. X=19 — наибольшая варианта, то F*(x)=1 при x>19
f(x) =
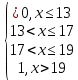
Задача 12. Задано распределение частот выборки:
| xi | 0,22 | 0,251 | 0,33 | 0,29 |
| ni | 1 | 6 | 8 | 13 |
Построить эмпирическую функцию распределения.
Вычислим объем выборки: n=1+6+8+13=28
Наименьшая варианта равна: x1=0.22, поэтому F*(x)=0 при x≤0.22
Значения X<0.251, а именно: x1=0.22, наблюдались 1 раз, следовательно, F*(x)=1/28= при 0.22< x≤0.251
Значения X<.033, а именно: x1=0.22, x2=0.251, наблюдались 7 раз, следовательно, F*(x)=7/28= при 0.251< x≤.033
Значения X<0.29, а именно: x1=0.22, x2=0.251, x3=.033, наблюдались 15 раз, следовательно, F*(x)=15/28= при .033< x≤0.29
Т.к. X=0.29 — наибольшая варианта, то F*(x)=1 при x>0.29
f(x) =