МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»

(наименование института полностью)

(Наименование учебного структурного подразделения)

20.03.01 Техносферная безопасность

(код и наименование направления подготовки / специальности)

Безопасность технологических процессов и производств

(направленность (профиль) / специализация)

Практическое задание №3
по учебному курсу «Высшая математика. Дифференциальное и интегральное исчисления»

^{(наименование учебного курса)}
Вариант 5 (при наличии)

Обучающегося	Пряничнеков Виталий Алексеевич
	(И.О. Фамилия)
Группа	ТБбп-2202а
Преподаватель	Кузнецова Ольга Александровна
	(И.О. Фамилия)

Тольятти 2023

Бланк выполнения задания №3

Вариант 5

---

Задача 3.1 Рассчитать наибольшее и наименьшее значения функции 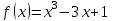на заданном отрезке [1/2;2]

Решение:

1) Найдем первую производную и все критические точки:



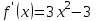
f(x) = 0 при х₁ = 1, х₂ = -1

В промежуток [1/2;2] попадает точка х = 1

2) Вычислим значения функции в критических точках:



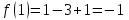
3) Вычислим значения функции на концах промежутка:

,

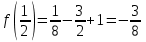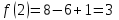
4) Сравним все полученные значения функции и выбрать среди них самое большое и самое малое:

Максимальное значение функции на отрезке [1/2;2] равно f_max = 3 при х = 2, минимальное значение – f_min = -1 при х = 1

Ответ: f_max = f(2) = 3, f_min = f(1) = -1.

Задача 3.2 Провести полное исследование и построить графики данных функций.

1)

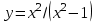
Решение:

1) Областью определения функции является множество всех вещественных чисел, кроме х = 1 и х = -1

При х  1-

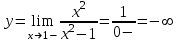
При х  1+

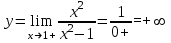
Так как f(1+) = f(1-) = , т.е. пределы функции неконечны, то точка х = 1 – точка разрыва второго рода.

При х  -1-

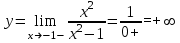
При х  -1+

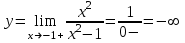
Так как f(-1+) = f(-1-) = , т.е. пределы функции неконечны, то точка х = -1 – точка разрыва второго рода.

2)

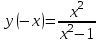
Так как у(-х) = у(х), то данная функция – четная, график функции симметричен относительно оси ординат.

Функция не является периодической.

3) 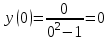- график функции проходит через начало координат

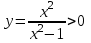при х  (-;-1)(1;+ ) и 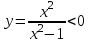при х  (-1;0)(0;1)

4) Найдем асимптоты:

Так как f(1+) = f(1-) = , то прямая х = 1 является вертикальной асимптотой графика

---

Так как f(-1+) = f(-1-) = , то прямая х = -1 является вертикальной асимптотой графика

При х  

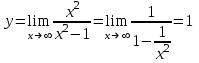
график имеет горизонтальную асимптоту у = 1.

5) Для нахождения точек возможного экстремума вычислим первую производную функции:



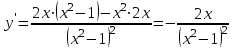
y = 0 при х = 0 и у =  при х = 1, х = -1

При х  (-;-1) у > 0 – функция возрастает, при х  (-1;0) у > 0 – функция возрастает, х = -1 – точка разрыва.

При х  (0;1) у < 0 – функция убывает, х = 0 – точка максимума, у(0) = 0.

При х  (1;+) у < 0 – функция убывает, х = 1 – точка разрыва.

6) Для нахождения точек возможного перегиба вычислим вторую производную функции:

Для нахождения точек возможного перегиба вычислим вторую производную функции:



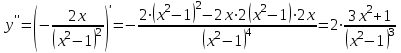
y =  при х = 1 и х = -1

При х  (-;-1) у > 0 – функция вогнутая,

при х  (-1;1) у < 0 – функция выпуклая,

х = -1 – точка разрыва.

При х  (1;+) у > 0 – функция вогнутая,

х = 1 – точка разрыва

7) Построим график, используя полученные результаты:



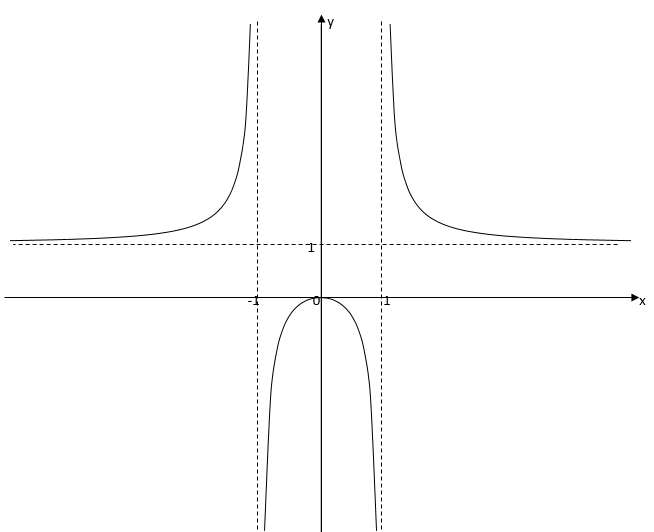
2)

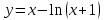
Решение:

1) Областью определения функции является множество всех вещественных чисел, удовлетворяющих условию х > -1

При х  -1

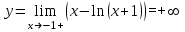
2)

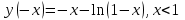
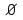
Так как у(-х)  у(х) и у(-х)  -у(х), то данная функция - функция общего вида.

Функция не является периодической.

3) у(0) = 0 - график функции проходит через начало координат

у > 0 при всех х > -1

4) Найдем асимптоты:

Так как при х  -1+ 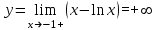, прямая у = -1 является вертикальной асимптотой графика

При х  +  ,

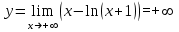график не имеет горизонтальных асимптот

---

При х  +  ,

,

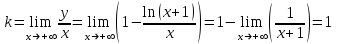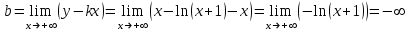график не имеет наклонных асимптот

5) Для нахождения точек возможного экстремума вычислим первую производную функции:



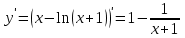
y = 0 при х = 0

При х  (-1;0) у < 0 – функция убывает, при х  (0;+) у > 0 – функция возрастает,

х = 0 – точка минимума, у(0) = 0.

6) Для нахождения точек возможного перегиба вычислим вторую производную функции:



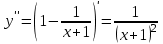
При х  (-1;+ ) у > 0 – функция вогнутая.

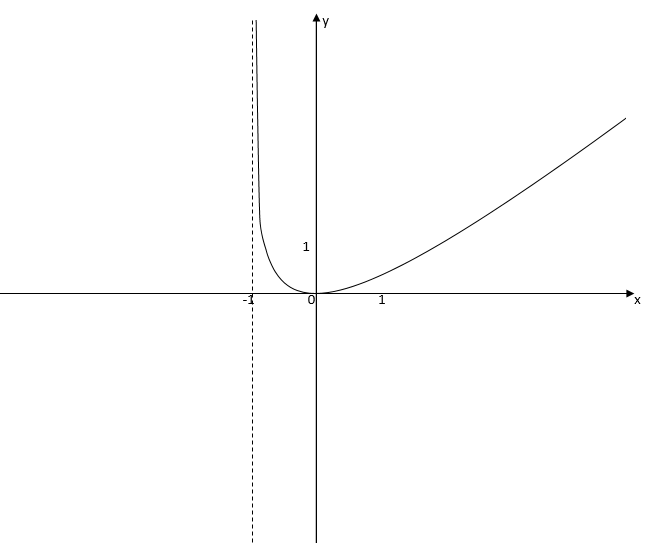
7) Построим график, используя полученные результаты:

---

Смотрите также файлы

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Психология Практическое занятие 3.doc

• Техническое задание информационной системы (В качестве предметной области выбрана тема Проектирование информационной системы "Поликлиника") Этап разработки раздела Общие сведения.docx

• А аргентометрия б броматометрия, бромометрия Г.docx

• Занятие 3 Тема занятия Освоение методики обучения строевым упражнениям детей дошкольного возраста.docx

• Направлениеспециальность подготовки 37.doc