Файл: Протокол от 20 г. Председатель Кудрявцева Е. П. Утверждаю Зам директора по учебной работе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 187
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Текстовые задачи (движение, работа, производительность)
-
Ремонт одного и того же автомобиля Виктор и Алексей делают за 8 дней, как и Андрей вместе с Виктором, при этом Алексей с Андреем могут выполнить этот ремонт за 12 дней. Сколько дней длиться ремонт, если все три автомеханика будут работать одновременно? -
На изготовление 27 деталей первый автослесарь тратит на 6 часов меньше, чем второй автослесарь на изготовлении 54 таких же деталей. Известно, что первый автослесарь за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй автослесарь? -
Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого па 12 км/ч, а вторую половину пути— со скоростью 72 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость перл i о ав томобиля, если известно, что она больше 45 км/ч. -
На АЗС первый насос наполняет емкость за 30 минут, второй - за 48 минут, а третий - за 1час 20 минут. За сколько минут наполнят емкость три насоса, работая одновременно?
-
Применение логарифмической и показательной функции в жизни и профессиональной деятельности
-
Количество автомобилей в городе возрастает ежегодно на 3%. Через сколько лет количество автомобилей в этом городе увеличиться в 1,5 раза? -
Какова была численность населения города 10 лет тому назад, если в настоящее время в городе проживает 300 тыс. человек, а ежегодный прирост составляет 3,5%?
-
Применение производной в практической и профессиональной деятельности
-
Закон прямолинейного движения задан уравнением s=-t3+9t2-24t-8. Найти максимальную скорость движения тела (.у- в метрах, t- в секундах). -
Требуется изготовить поддон для слива отработанного ГСМ - открытую сверху коробку, вырезая по углам равные квадратики. Прямоугольный лист жести имеет длину 64 см и ширину 40 см. Каковы должны быть стороны вырезаемых квадратиков, чтобы вместимость поддона была максимальной. -
Я хотел подзаработать на продаже газет. На соседнем углу дневной спрос- прямая линия. При этом если цена газеты 12,5 рублей, то газеты не берут вовсе, а больше 50 газет продать не удаётся никогда. Тётя Клава, которая работает в типографии, сказала, что даст мне столько газет, сколько надо за коробку конфет, а Витька, мой конкурент из параллельного класса, сказал, что даст мне 30 рублей, если я вовсе не появлюсь на том углу со своими газетами.
-
Геометрические задачи
-
Кузов тракторного прицепа имеет форму усеченной пирамиды и размеры: вверху 3,5 м х 2,6 м, понизу 2,9 м х 1,1 м. Найдите вместимость, если высота прицепа 1,2 м. -
На цилиндрический барабан подъемной машины, диаметр которого 750 мм, а ширина 350 мм, наматывается стальной трос толщиной 20 мм. Сколько метров каната помещается в один ряд на поверхности барабана?
Раздел 2. Ответы, решения.
-
Целые, рациональные и дробные числа
-
Решение: 33 рубля 62 коп. = 33,62 рублей.
Стоимость покупки составила 25*33,62==840,5 рублей.
Следовательно, водитель должен получить 1 000—840,5=159,5 рублей сдачи.
Ответ: 159 рублей 50 коп.
-
12 флаконов. -
25. -
14. -
24
-
Задачи на проценты
-
1500 рублей. -
на 24%. -
21. -
20000 рублей. -
Решение. Пусть а – первоначальная цена товара. После повышения цены, товар стал стоить а + 0,25а =1,25а, найдем отношения первоначальной цены товара к его новой цене и выразим это отношение в процентах: Значит, новую цену товара надо снизить на 20% (100% - 80%=20%).
Ответ: новую цену товара надо снизить на 20%
-
Решение. Так как сухие грибы содержат воду -12%, то 22 кг составляют 88% от массы сухих грибов, полученных из 22кг свежих грибов. Отсюда -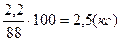 масса сухих грибов.
масса сухих грибов.
Ответ: 2,5 (кг) - масса сухих грибов.
-
Пусть всхожесть семян можно найти так: разделить 1800 на r(%). Тогда один процент всхожести семян можно найти так: разделить 1800 на r или 2000 на 100. Отсюда 1800/r= 2000/100. найдем неизвестный средний член этой пропорции.
Ответ: r = 90%
-
2500 руб. -
Пусть ежедневная норма х листов, а срок окончания работы у дней; тогда работа содержит х·у листов. По условию, вырабатывая в день х+2 листа, оператор затратит у-2 дня. Значит, работа содержит (х+2) (у-2) листов. Следовательно, (х+2)(у-2)=ху. Таким же образом получаем другое уравнение (х+0,6х)(у-4)=ху+8.
Ответ: норма 10 листов в день; срок исполнения 12 дней.
-
Текстовые задачи (движение, работа, производительность)
-
6 дней. -
57 км/ч. -
48 км/ч. -
15 минут.
-
Применение логарифмической и показательной функции в жизни и профессиональной деятельности
-
Для решения этой задачи применим формулу сложных процентов, составим показательное уравнение и прологарифмируем его.
Ответ: примерно через 14 лет.
-
Решение: численность населения изменяется по формуле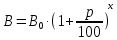 . в нашей задаче В=300 тыс. человек, р=3,5 %, х=10 лет,
. в нашей задаче В=300 тыс. человек, р=3,5 %, х=10 лет, 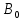 - численность населения 10 лет тому назад. Тогда
- численность населения 10 лет тому назад. Тогда 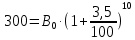 ; 300=
; 300=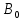 •1,03510 ; В0=
•1,03510 ; В0=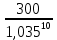 ≈212,7 тысяч человек.
≈212,7 тысяч человек.
Ответ: численность населения 10 лет назад равна 212,7 тыс. человек
Вывод: Практическое применение логарифмов связано с их возможностью описывать процессы, при которых изменение одной величины в некоторое количество раз ведёт к изменению зависимой величины на некоторое количество раз. Или наоборот, одна величина меняется на, а другая изменяется в. Таким законам подчиняются, например, процессы размножения микроорганизмов, рост колоний бактерий, радиоактивный распад элементов, изменение скоростей химических реакций и т.п. Все эти процессы получили название процессов органического роста, поскольку их математическая модель имеет одну и ту же структуру.
-
Применение производной в практической и профессиональной деятельности
-
Решение: v = s′(t) = -3t2 + 18t - 24; -3t2 + 18t – 24= 0; t1=4; t2=2; v(2)=0; v(3)=3; v(4)=0. -
Решение: V=(64-2x)*(40-2x)*x. V’(x)=12x2-416x+2560, 3x2-104x+640=0; D=3136, Отсюда xi=l60/6=80/3 превышает 26 и лишено смысла , хг=8
Ответ: 8 см.
-
Решение: 1) Определим функцию спроса, т.е. определим, по какому закону продаются газеты. График уравнения, описывающего закон продаж должен проходить через точки (12,5 ; 0) и (0 ; 50), значит это будет линейная зависимость. Q(P)= kP+b
-
при Р = 0 , а Q = 50 получаем, что k*0+b= 50, значит b=50. -
при P = 12,5, а Q= 0 получаем, что 12,5 k+ 50 = 0, значит k = -4 -
объём продаж будет выражаться формулой: Q(P) = - 4P+ 50
2) По условию задачи бизнес следует начинать если прибыль будет наибольшей, значит нам следует найти наибольшую величину прибыли ( выручки).
3) Обозначим прибыль через R(P).
4) Найдём наибольшее значение выручки на промежутке (0, 12,5)
Вывод: Производная является важнейшим инструментом экономического анализа. При помощи производной можно значительно расширить круг рассматриваемых при решении задач функций. Экономический смысл производной состоит в следующем: производная выступает как скорость изменения некоторого экономического процесса с течением времени или относительно другого исследуемого фактора. Производная находит широкое приложение в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических. Знание производной позволяет решать многочисленные задачи по экономической теории
2.6 Геометрические задачи
-
7м3 . -
412 м.
Раздел 3. Справочные материалы.
-
Алгебра
Таблица квадратов натуральных чисел от 0 до 99
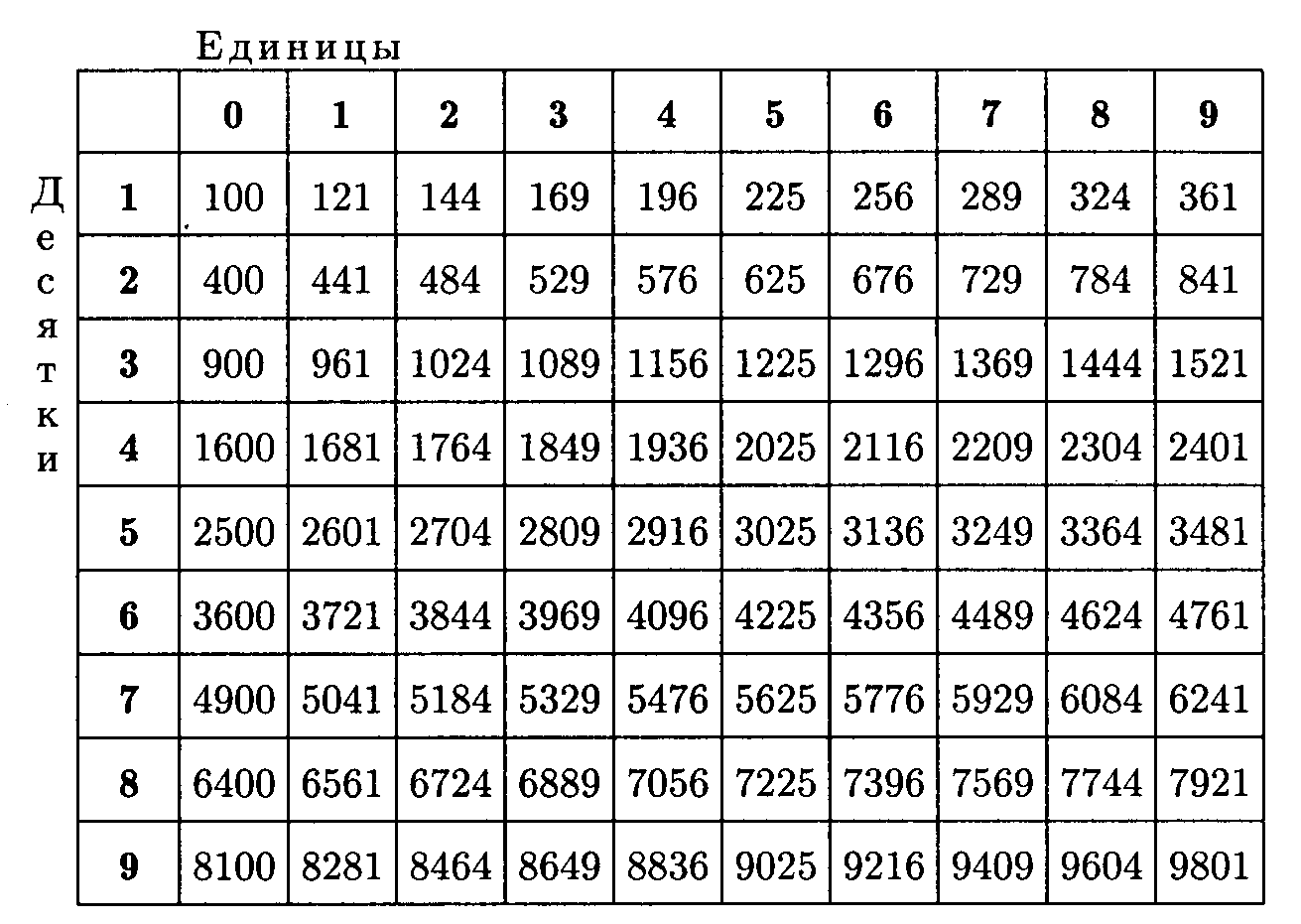
Свойства арифметического квадратного корня

Процент — это одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому.
Простые проценты – это метод начисления, при котором сумма процентов определяется в течение всего периода, исходя из первоначальной величины долга, независимо от количества периодов начисления и их длительности. Формула расчета выглядит так: S = а * ( (1 + у * х)/ 100), где a — исходная сумма, S — сумма, которая наращивается, x — процентная ставка, y — количество периодов начисления процента.
Сложные проценты — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Формула расчета выглядит так: SUM = X * (1 + %)n, где SUM — конечная сумма; X — начальная сумма; % — процентная ставка, процентов годовых /100; n — количество периодов, лет (месяцев, кварталов).
Свойства логарифмов.
-
logax+ logay= loga(x·y); -
logax− logay= loga(x:y). -
logaxn=n· logax; -
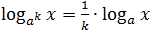
-
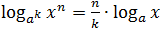
-
Геометрия.
Соотношения между тригонометрическими функциями
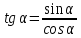 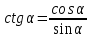 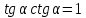 | 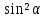 + +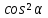 =1 – основное тригонометрическое тождество =1 – основное тригонометрическое тождество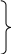  формулы приведения 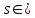 (90 ̊– α) = (90 ̊– α) = 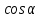 cos(90 ̊ – α) = 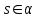 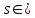 (180 ̊– α) = (180 ̊– α) = 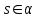 cos(180 ̊– α) = – 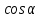 |
Значения синуса, косинуса и тангенса некоторых углов.
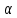 | 30 ̊ | 45 ̊ | 60 ̊ |
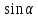 | 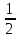 | 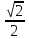 | 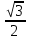 |
 | 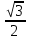 | 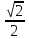 | 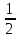 |
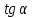 | 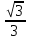 | 1 | 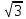 |
Список литературы
Основная
-
Башмаков М.И. Математика: алгебра и качала математического анализа, геометрия. Издательский центр «Академия» 2017
Дополнительная
-
Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: В двух частях.Ч.1: Учеб, для общеобразоват. учреждений (базовый уровень) - 9-е изд. -М.: Мнемозина, -
Математика: Справ. Материалы: Кн. для учащихся, - М.: Просвещение, 2001- 416 с. -
Изучение алгебры и начал анализа в 10-1! классах: Кн. для учителя / Н. Е. Федорова,. Г, Ткачева. - 2-е изд- М.: Просвещение, 2004.