Файл: Отчет по учебной практике обучающийся гр. Катп21 аббревиатура группы 01. 06. 2023.docx
Добавлен: 25.10.2023
Просмотров: 125
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Диаграмма является основной единицей описания в IDEF3. Важно правильно построить диаграммы, поскольку они предназначены для чтения другими людьми (а не только автором).
С помощью диаграмм IDEF3 можно анализировать сценарии из реальной жизни, например, как закрывать магазин в экстренных случаях или какие действия должны выполнить менеджер и продавец при закрытии. Каждый такой сценарий содержит в себе описание процесса и может быть использован, что бы наглядно показать или лучше задокументировать бизнес-функции организации.
Модель, выполненная в IDEF3, может содержать следующие элементы:
Единицы работы (Unit of Work) - основной компонент диаграммы IDEF3 близкий по смыслу к работе IDEF0. В IDEF3 работы изображаются прямоугольниками с прямыми углами и имеют имя, выраженное отглагольным существительным, обозначающим процесс действия, одиночным или в составе фразы, и номер (идентификатор); другое имя существительное в составе той же фразы обычно отображает основной выход (результат) работы (например, "Изготовление изделия"). Часто имя существительное в имени работы меняется в процессе моделирования, поскольку модель может уточняться и редактироваться. Идентификатор работы присваивается при создании и не меняется никогда. Даже если работа будет удалена, ее идентификатор не будет вновь использоваться для других работ. Обычно номер работы состоит из номера родительской работы и порядкового номера на текущей диаграмме.
В IDEF3 различают три типа связей:
Связь предшествования (Precedence) – показывает, что прежде чем начнется работа-приемник, должна завершиться работа-источник. Обозначается сплошной линией.
Связь отношения (Relational) - показывает связь между двумя работами или между работой и объектом ссылки. Обозначается пунктирной линией.
Связь поток объектов (Object Flow) – показывает участие некоторого объекта в двух или более работах, как, например, если объект производится в ходе выполнения одной работы и потребляется другой работой. Обозначается стрелкой с двумя наконечниками.
Перекрестки (соединения) - перекрестки используются в диаграммах IDEF3, чтобы показать ветвления логической схемы моделируемого процесса и альтернативные пути развития процесса могущие возникнуть во время его выполнения. Окончание одной работы может служить сигналом к началу нескольких работ, или же одна работа для своего запуска может ожидать окончания нескольких работ. Перекрестки используются для отображения логики взаимодействия стрелок при слиянии и разветвлении или для отображения множества событий, которые могут или должны быть завершены перед началом следующей работы.
Формальные методы реинжиниринга бизнес-процессов основаны на четырехуровневой графовой модели бизнес-процесса, включающей в себя: уровень информационных объектов, уровень бизнес-операций, уровень бизнес-функций и уровень бизнес-процесса. Такая модель отражает: организационно-штатную структуру предприятия, бизнес-процессы его деятельности (пронизывающие структуру предприятия по горизонтали), сведения о ресурсах, которыми располагает предприятие. В эту модель транслируются полученные в результате предпроектного анализа традиционные модели, такие, как диаграммы потоков данных, SADT -диаграммы, диаграммы «Сущность-связь», диаграммы переходов состояний.
Для построения любой традиционной модели используются три уровня анализа:
· определение требований;
· формирование спецификаций;
· описания реализации.
На основе сформулированных требований, можно провести следующую классификацию инструментальных средств, используемых для моделирования бизнес-процессов при реинжиниринге бизнеса: инструментальные средства создания диаграмм и инструментарий низкого уровня; CASE, структурный и объектно-ориентированный инструментарий; средства имитационного моделирования/анимации; средства стоимостного анализа бизнес-процессов; интегрированные многофункциональные средства.
-
Пример компьютерного моделирования на производстве
Построение математической модели на основе детерминированного подхода
Построим математическую модель канальной индукционной печи, используя детерминированный подход. Это означает, что для построения мы будем использовать физические законы.
Нагрев осуществляется по закону Джоуля-Ленца:
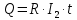 (1)
(1)Так как мощность
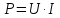 , а
, а 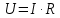 , то можно преобразовать выражение (1) в:
, то можно преобразовать выражение (1) в: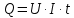 (2)
(2)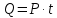
(3)
Тепло от дуги должно передаться содержимому. Основное уравнение теплопередачи:
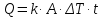 (4)
(4)где Q – количество теплоты, Дж;
K – коэффициент теплопередачи;
A – площадь поверхности теплообмена, м3;
ΔT – разница температур, К;
t – время, с.
Приравняем формулы (3) и (4) и получим зависимость мощности и температуры:
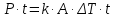 (5)
(5)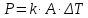 (6)
(6)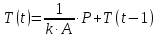 (7)
(7)Таким образом мы получили функцию модели объекта. Модель представляет собой интегрирующее функциональное звено. На вход звена подаются мощность тока P, площадь поверхности теплообмена A, коэффициент теплопередачи k, а также предыдущее выходное значение T.
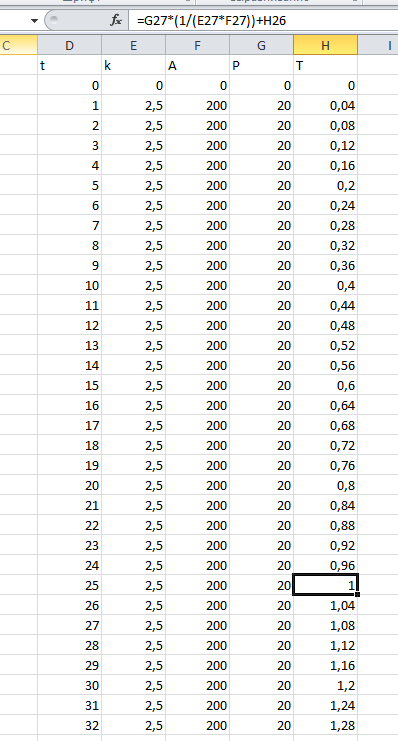
Рисунок 4 – Реализация модели в Microsoft Excel
На рисунке 3 можно увидеть, как на вход объекта подаются постоянные k (столбец E), A (столбец F) и P (столбец G). Выходное значение T (столбец H) постоянно увеличивается. В ячейке H3 можно увидеть формулу, которую содержат все остальные ячейки в столбце H.
Линейный регрессионный анализ
Регрессионный анализ (regression analysis) – это метод изучения статистической взаимосвязи между одной зависимой количественной зависимой переменной от одной или нескольких независимых количественных переменных. Зависимая переменная в регрессионном анализе называется результирующей, а переменные факторы – предикторами или объясняющими переменными.
Взаимосвязь между средним значением результирующей переменной и средними значениями предикторов выражается в виде уравнения регрессии. Уравнение регрессии – математическая функция, которая подбирается на основе исходных статистических данных зависимой и объясняющих переменных. Чаще всего используется линейная функция. В этом случае говорят о линейном регрессионном анализе.
Регрессионный анализ очень тесно связан с корреляционным анализом. В корреляционном анализе исследуется направление и теснота связи между количественными переменными. В регрессионном анализе исследуется форма зависимости между количественными переменными. Т.е. фактически оба метода изучают одну и ту же взаимосвязь, но с разных сторон, и дополняют друг друга. На практике корреляционный анализ выполняется перед регрессионным анализом. После доказательства наличия взаимосвязи методом корреляционного анализа можно выразить форму этой связи с помощью регрессионного анализа.
Цель регрессионного анализа – с помощью уравнения регрессии предсказать ожидаемое среднее значение результирующей переменной.
Основные задачи регрессионного анализа следующие:
-
определения вида и формы зависимости; -
оценка параметров уравнения регрессии; -
проверка значимости уравнения регрессии; -
проверка значимости отдельных коэффициентов уравнения; -
построение интервальных оценок коэффициентов; -
исследование характеристик точности модели; -
построение точечных и интервальных прогнозов результирующей переменной.
Как и корреляционный анализ, регрессионный анализ отражает только количественные зависимости между переменными. Причинно-следственные зависимости регрессионный анализ не отражает. Гипотезы о причинно-следственной связи переменных должны формулироваться и обосновываться исходя из теоретического анализа содержания изучаемого явления
Построение модели с помощью регрессионного анализа
Построим модель, используя регрессионный анализ. Известна модель сигнала:
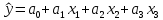 (8)
(8)Необходимо определить значения коэффициентов
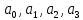 . Для этого необходимо провести не менее 30 наблюдений и, воспользовавшись предложенными методами обработки наблюдений, определить коэффициенты.
. Для этого необходимо провести не менее 30 наблюдений и, воспользовавшись предложенными методами обработки наблюдений, определить коэффициенты.В качестве натурных данных возьмем параметры, полученные от первой модели. Всего взято 60 опытов.
Для поиска коэффициентов воспользуемся методом наименьших квадратов в матричной форме:
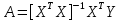 (9)
(9)где
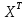 – транспонированная матрица входных переменных.
– транспонированная матрица входных переменных.Для использования метода наименьших квадратов необходимо соблюдать его предпосылки:
1. Распределение случайных величин должно соответствовать нормальному.
2. Дисперсия должна быть минимальной и постоянной.
3. Математическое ожидание должно быть равно нулю, а его оценка несмещенной.
Для дальнейшего расчета необходимо добавить столбец x0 к матрице параметров, где все значения равны единице. Затем полученную матрицу
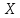
= 510х4 транспонировать в матрицу
 = 4х510. Далее по формуле выше проделать действия и получить матрицу 4х1 из нужных коэффициентов (таблица 2).
= 4х510. Далее по формуле выше проделать действия и получить матрицу 4х1 из нужных коэффициентов (таблица 2). Таблица 2- Результаты расчета по методу наименьших квадратов
| Коэффициент | Значение |
| A0 | 4,41164414637775 |
| A1 | -0,667976768979025 |
| A2 | -0,668841424108692 |
| A3 | 0,180119047619048 |
При данных коэффициентах S=4,6
Метод взвешенных наименьших квадратов
Для использования метода наименьших квадратов необходимо соблюдать его предпосылки:
1. Распределение случайных величин должно соответствовать нормальному.
2. Дисперсия должна быть минимальной и постоянной.
3. Математическое ожидание должно быть равно нулю, а его оценка несмещенной.
Но иногда дисперсия может быть не постоянной на всем промежутке значений. Для того чтобы нивелировать непостоянство дисперсии необходимо воспользоваться методом взвешенных наименьших квадратов в матричной форме:
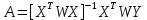 (10)
(10)где
 – транспонированная матрица входных переменных.
– транспонированная матрица входных переменных.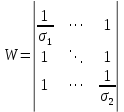 – матрица сужения дисперсии.
– матрица сужения дисперсии.Аналогично расчётам второй практической проводим вычисления добавив матрицу W. Результаты представлены в таблице 3. Так же в таблице 3 для сравнения показаны коэффициенты, полученные в результате применения обычного МНК, также абсолютная разница между коэффициентами обоих методов.
Таблица 3 – Результаты расчета по методу наименьших квадратов
| Коэффициент | МВНК | МНК | Разница |
| b0 | 14,5 | 4,4 | 10,1 |
| b1 | -1,1 | -0,6 | 0,5 |
| b2 | -1,2 | -0,6 | 0,6 |
| b3 | 0,9 | 0,1 | 0,8 |