ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 64
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
где: q2 , q3 - вероятности (частоты) с которыми применяются соответственно стратегии B2 и B3
Из теории игр известно, что если игрок "B" использует свою оптимальную стратегию, а игрок "A" остается в рамках своих активных стратегий, то средний выигрыш остается неизменным и равным цене игры v независимо от того как игрок "А" использует свои активные стратегии. Поэтому если предположить, что игрок "A" будет пользоваться чистой стратегией A1, то средний выигрыш v составит:
k12q2 + k13q3 = v ( 4 )
Поскольку цена игры v нам уже известна и учитывая, что q2 + q3 = 1, то оптимальная частота стратегии B2 может быть найдена как:
| q2 = |
| ( 5 ) |
В данной задаче:
| q2 = |
| = |
|
Вероятность q
3 найдем вычитанием q2 из единицы:
| q3 = 1 - q2 = | 1 | - |
| = |
|
Ответ:
| Нижняя цена игры : | α = | 3 | |||
| Верхняя цена игры : | β = | 4 | |||
| Цена игры : | v = |
|
| Оптимальная стратегия игрока "А" : |
| |||||||||||||||
| Оптимальная стратегия игрока "B" : |
|
Геометрическая интерпретация (графическое решение):
Дадим геометрическую интерпретацию рассмотренной игре. Возьмем участок оси абсцисс единичной длины и проведем через его концы вертикальные прямые a1 и a3 соответствующие нашим стратегиям A1 и A3. Предположим теперь, что игрок "B" будет пользоваться стратегией B2 в чистом виде. Тогда, если мы (игрок "A") будем использовать чистую стратегию A1, то наш выигрыш составит 4.Отметим соответствующую ему точку на оси a1.
Если же мы будем использовать чистую стратегию A3, то наш выигрыш составит 1. Отметим соответствующую ему точку на оси a3
(см. Рис. 1). Очевидно, если мы будем применять, смешивая в различных пропорциях стратегии A1 и A3, наш выигрыш будет меняться по прямой проходящей через точки с координатами (0 , 4) и (1 , 1), назовем ее линией стратегии B2 (на Рис.1 показана красным цветом). Абсцисса любой точки на данной прямой равна вероятности p3 (частоте), с которой мы применяем стратегию A3, а ордината - получаемому при этом выигрышу k (см. Рис.1).
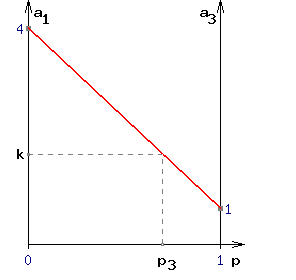
Рисунок 1.
График зависимости выигрыша k от частоты р3, при использовании противником стратегии B2.
Предположим теперь, что игрок "B" будет пользоваться стратегией B3 в чистом виде. Тогда, если мы (игрок "A") будем использовать чистую стратегию A1, то наш выигрыш составит 3.Если же мы будем использовать чистую стратегию A3, то наш выигрыш составит 4 (см. Рис. 2). Аналогично, если мы будем смешивать в различных пропорциях стратегии A1 и A3, наш выигрыш будет меняться по прямой проходящей через точки с координатами (0 , 3) и (1 , 4), назовем ее линией стратегии B3. Как и в предыдущем случае, абсцисса любой точки на этой прямой равна вероятности, с которой мы применяем стратегию A3, а ордината - получаемому при этом выигрышу, но только для стратегии B
3 (см. Рис. 2).
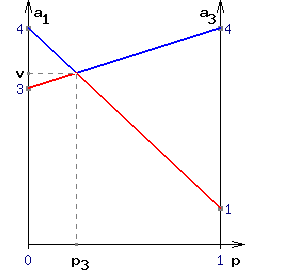
Рисунок 2.
Графическое определение цены игры v и оптимальной частоты р3 для игрока "А".
В реальной игре, когда разумный игрок "В" пользуется всеми своими стратегиями, наш выигрыш будет изменяться по ломаной линии, показанной на Рис.2 красным цветом. Эта линия определяет так называемую нижнюю границу выигрыша. Очевидно, что самая высокая точка этой ломанной соответствует нашей оптимальной стратегии. В данном случае, это точка пересечения линий стратегий B2и B3. Обратите внимание, что если выбрать частоту p3 равной ее абсциссе, то наш выигрыш будет оставаться неизменным и равным vпри любой стратегии игрока "B", кроме того он будет максимальным который мы можем себе гарантировать. Частота (вероятность) p3, в этом случае, есть соответствующая частота нашей оптимальной смешанной стратегии. Кстати из рисунка 2 видна и частота p1, нашей оптимальной смешанной стратегии, это длина отрезка [p3 ; 1] на оси абсцисс. (Это потому, что p1 + p3 = 1 )
Совершенно аналогично рассуждая, можно найти и частоты оптимальной стратегии для игрока "В", что иллюстрируется на рисунке 3.
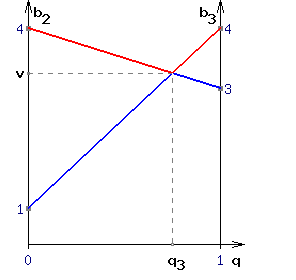
Рисунок 3.
Графическое определение цены игры v и оптимальной частоты q3 для игрока "В".
Только для него следует построить так называемую верхнюю границу проигрыша (красная ломаная линия) и искать на ней самую низкую точку, т.к. для игрока "В" цель, это минимизация проигрыша. Аналогично значение частоты q2, это длина отрезка [q3 ; 1] на оси абсцисс.