ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Раздел 1. Комплексные числа.
1.1. Построение системы комплексных чисел.
1.1.1 Основные определения.
Пару
Определение 1. Комплексным числом называется любая упорядоченная пара
Множество всех комплексных чисел обозначается С.
Определение 2. Два комплексных числа
пишут
Условимся в дальнейшем комплексные числа обозначать строчными буквами греческого алфавита.
Определение 3. Пусть
Сумма
а произведение
Операции сложения и умножения комплексных чисел обладают следующими свойствами:
-
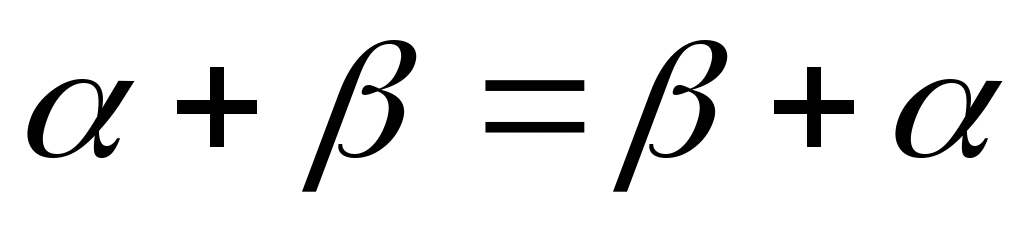 (коммутативность сложения.)
(коммутативность сложения.) -
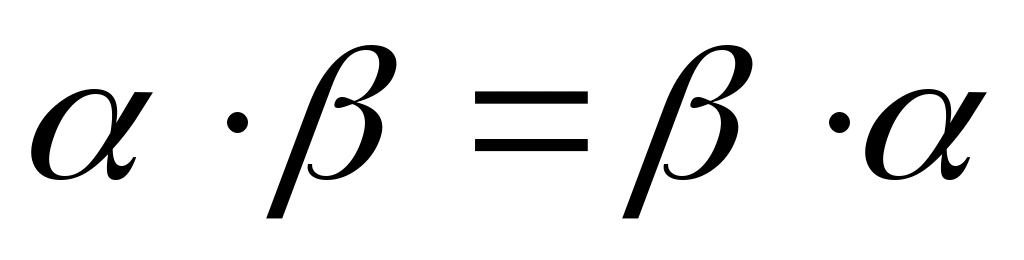 (коммутативность умножения).
(коммутативность умножения). -
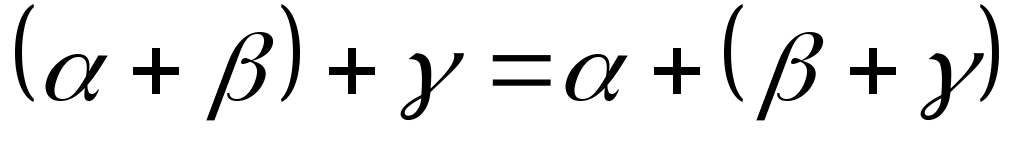 (ассоциативность сложения).
(ассоциативность сложения). -
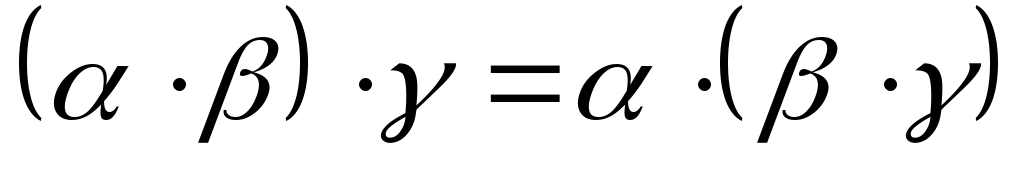 (ассоциативность умножения).
(ассоциативность умножения). -
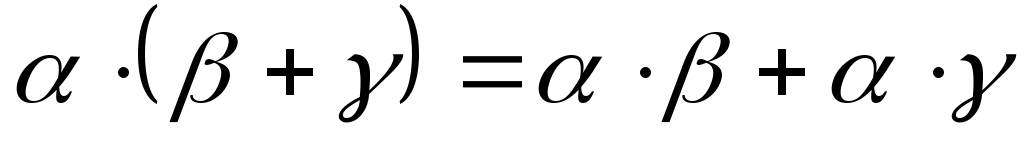 (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
Упражнение. Проверить свойства 1-5.
Упорядоченная пара
Определение 4. Пусть
Разностью
упорядоченную пару
Найдем x и y. Поскольку
Таким образом, вычитание упорядоченных пар определяется формулой
Определение 5. Частным
Найдем x и y. Так как
, то
Из последнего равенства при
Значит, роль единицы при делении упорядоченных пар выполняет упорядоченная пара
1.1.2 Множество комплексных чисел как расширение множества действительных чисел.
Рассмотрим комплексные числа вида
Если каждому действительному числу а сопоставим комплексное число
Для любых двух действительных чисел а и bимеем
То же самое относится к произведению: так как
Из сказанного следует, что если отождествить каждое действительное число а с комплексным числом
1.1.3 Алгебраическая форма комплексного числа.
Арифметические действия над комплексными числами.
Сопряженные комплексные числа. Свойства операции сопряжения.
Условимся в дальнейшем не делать различия между комплексным числом вида
Рассмотрим упорядоченную пару
Определение 6. Упорядоченную пару
соотношению
С помощью мнимой единицы можно выразить любое комплексное число. В самом деле, так как
то
Теперь можно забыть о первоначальном способе задания комплексного числа как пары
Определение 7. Выражение
комплексного числа. Число а называют действительной частью,
число b – мнимой частью комплексного числа
Если задано комплексное число
Если
Определение 8.Пусть
знаком коэффициента при мнимой части, называется
сопряженнымчислу