ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Итак, по определению,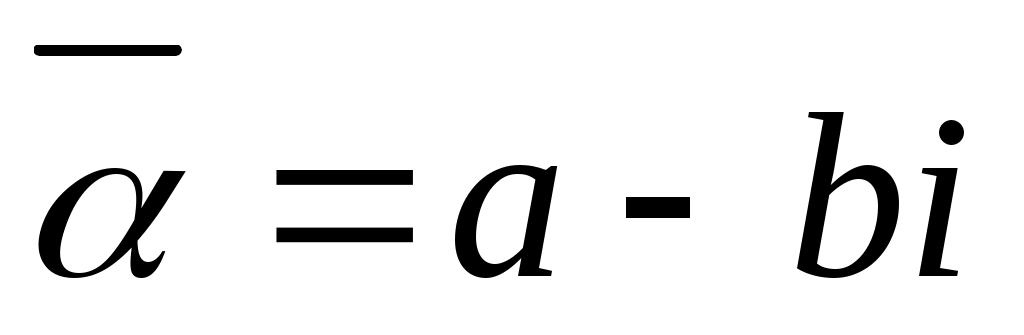 .
.
Если - действительное число, т.е.
- действительное число, т.е. 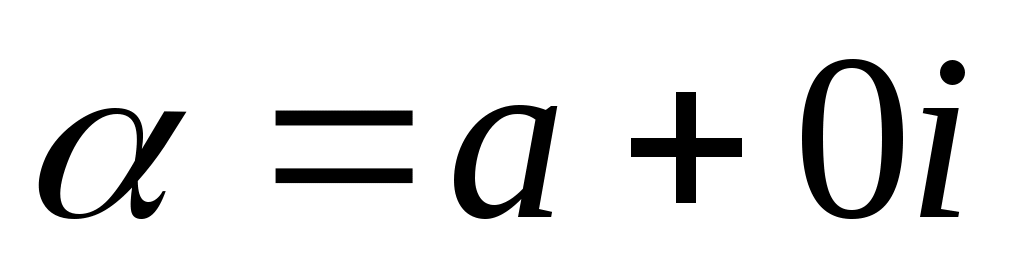 , то
, то 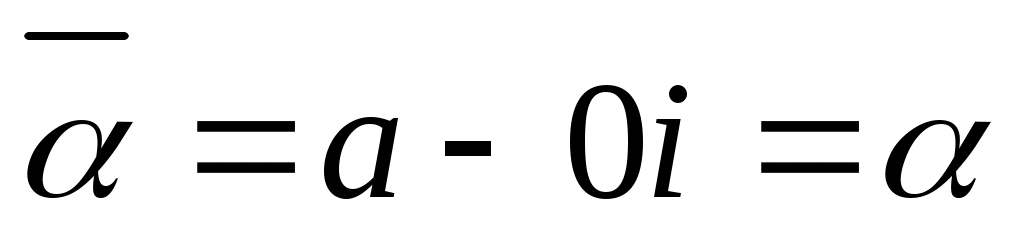 . Таким образом, любое действительное число равно своему сопряженному.
. Таким образом, любое действительное число равно своему сопряженному.
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами следует, что
1.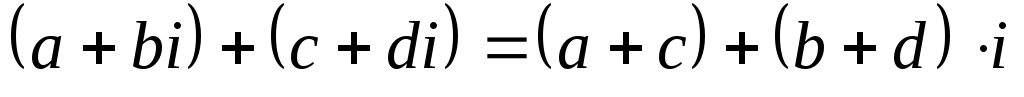 ,
,
2.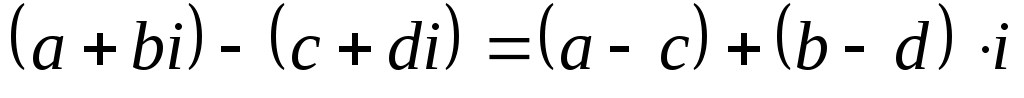 ,
,
3.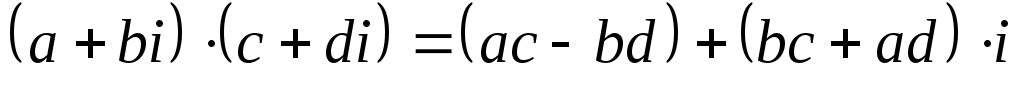 ,
,
4.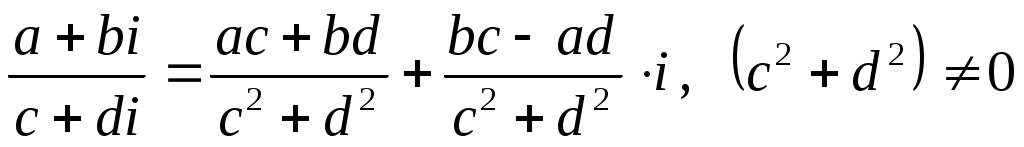 .
.
Формула 1 определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула 2 означает, что при вычитании одного комплексного числа из другого, необходимо вычесть отдельно их действительные и мнимые части.
Формулу 3 можно получить путем умножения по правилам алгебры и замены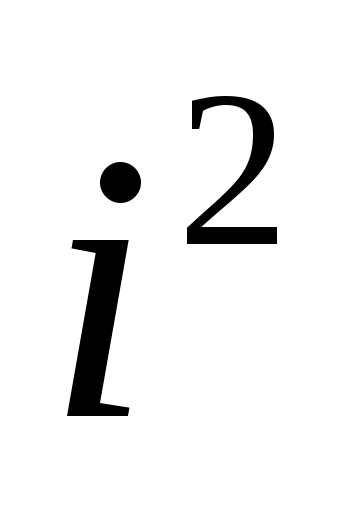 его значением:
его значением:
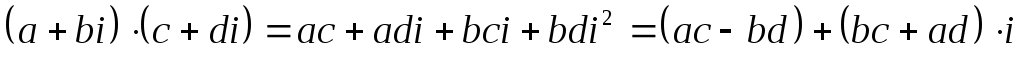 .
.
Чтобы получить формулу 4, необходимо предварительно числитель и знаменатель умножить на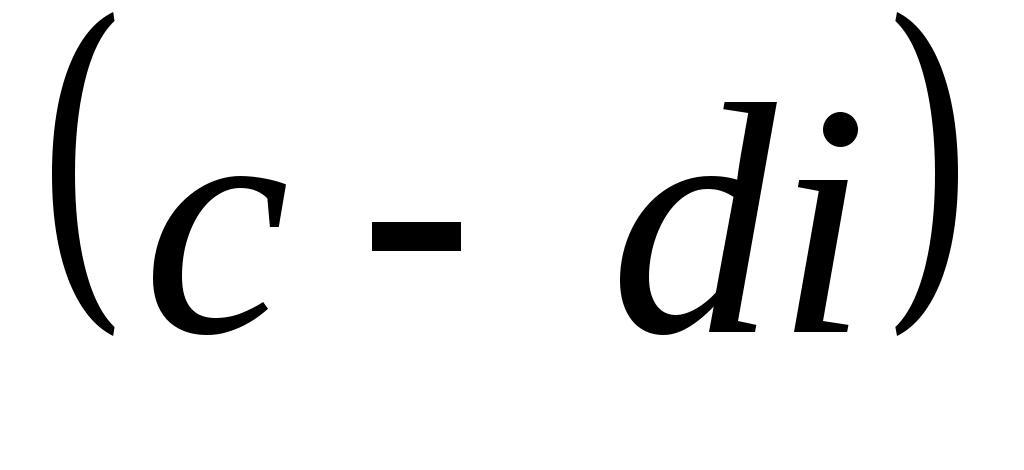 (число сопряженное числу
(число сопряженное числу 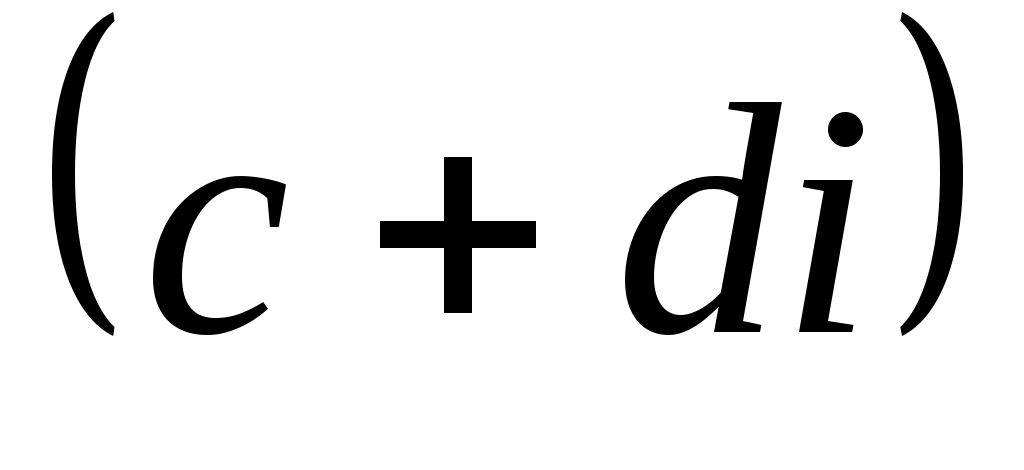 ):
): 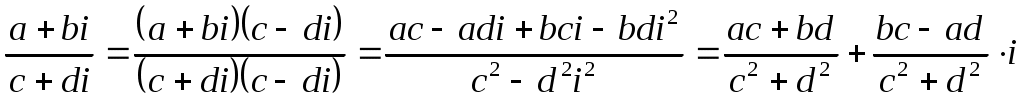 .
.
Сформулируем основные свойства операции сопряжения:
1)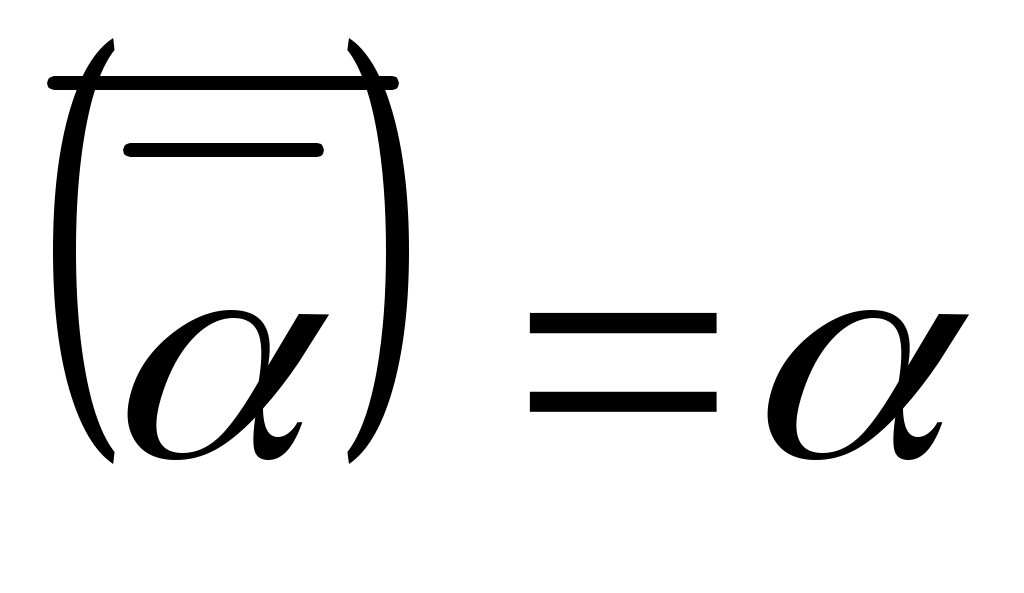 ; 4)
; 4) 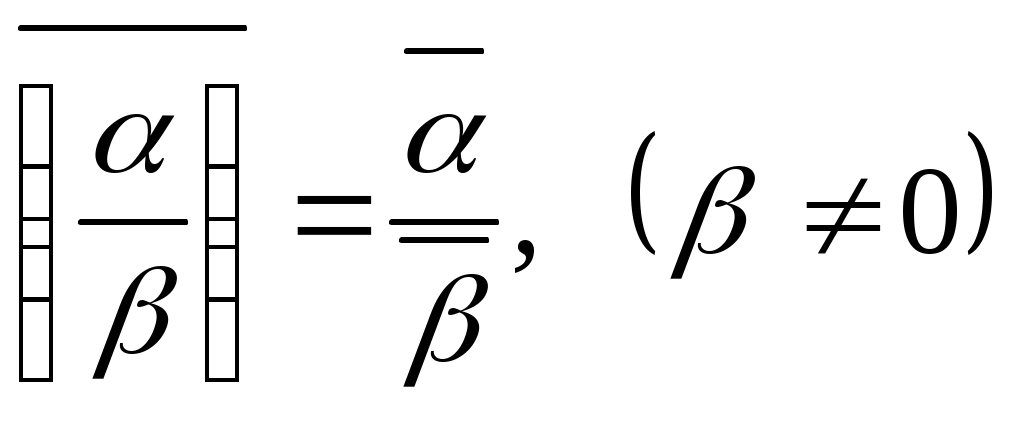 ;
;
2)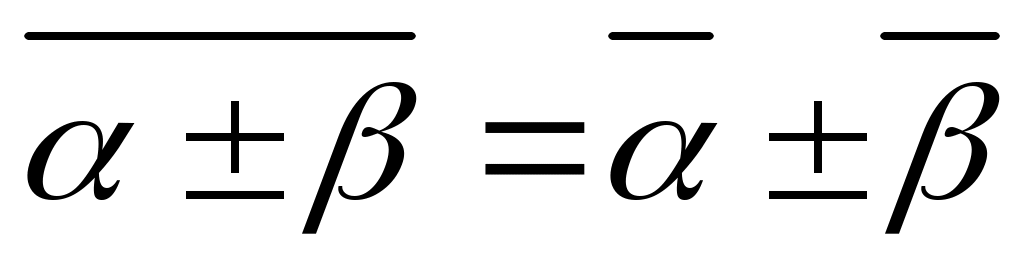 ; 5)
; 5) 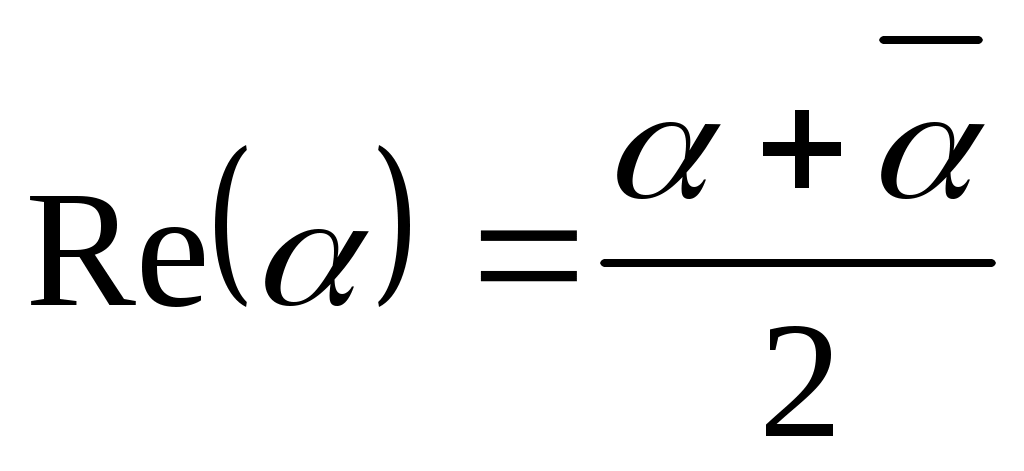 ;
;
3)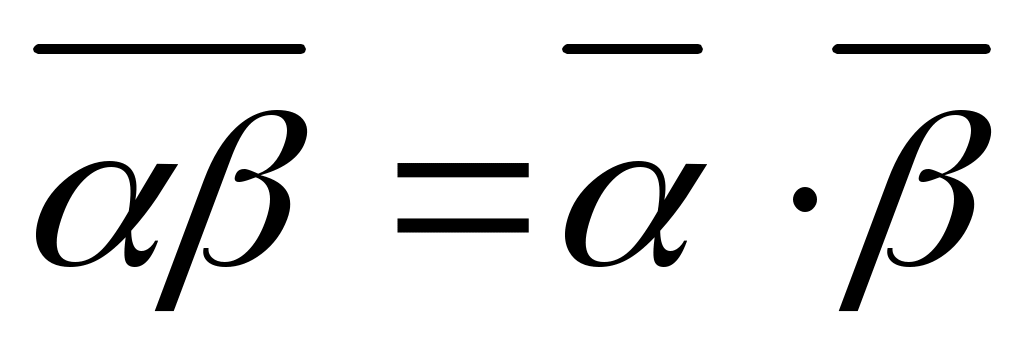
; 6)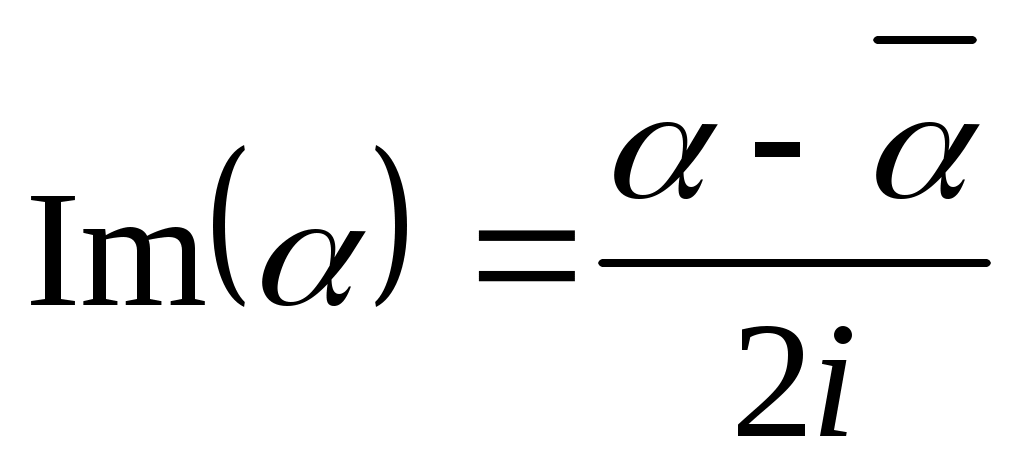 .
.
Упражнение 2. Доказать свойства 1-5 операции сопряжения.
1.1.4 Геометрическое изображение комплексных чисел. Комплексная плоскость.
Если для изображения действительных чисел используются точки числовой прямой, то изображениями комплексных чисел служат точки координатной плоскости.
Введем на плоскости прямоугольную декартову систему координат с осями х и у. Тогда каждому комплексному числу будет отвечать точка с координатами
будет отвечать точка с координатами  . Эту точку чаще всего обозначают той же буквой
. Эту точку чаще всего обозначают той же буквой  , что и само число.
, что и само число.
При таком способе изображения комплексных чисел любому действительному числу, т.е. числу вида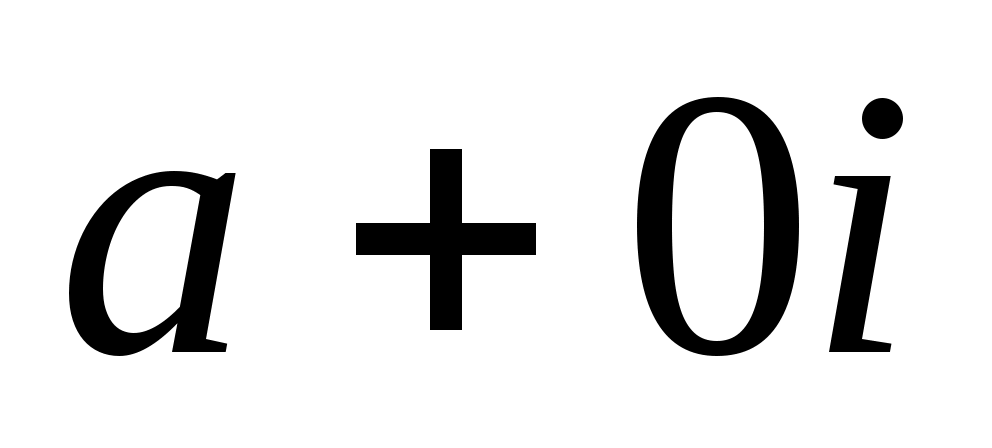 , отвечает точка
, отвечает точка  , лежащая на оси х. Таким образом, приходим к уже известному способу изображения действительных чисел точками числовой прямой х. В связи с этим ось х называют действительной осью. Комплексным же числам вида
, лежащая на оси х. Таким образом, приходим к уже известному способу изображения действительных чисел точками числовой прямой х. В связи с этим ось х называют действительной осью. Комплексным же числам вида 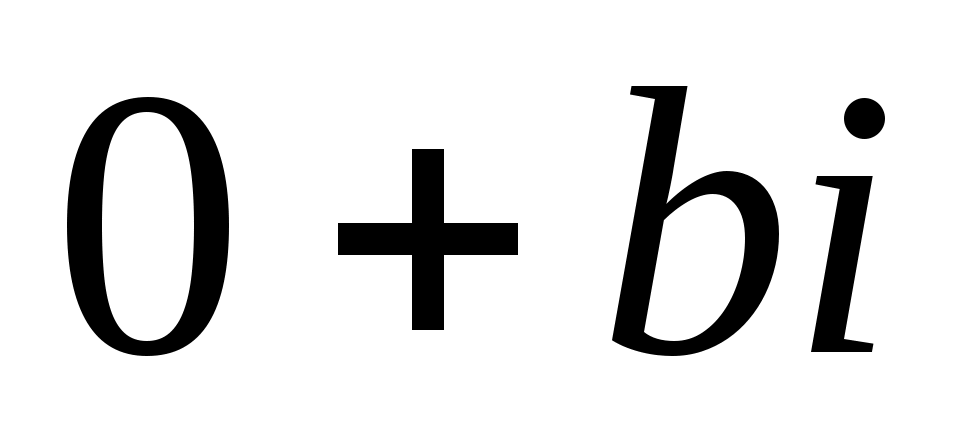 отвечают точки
отвечают точки 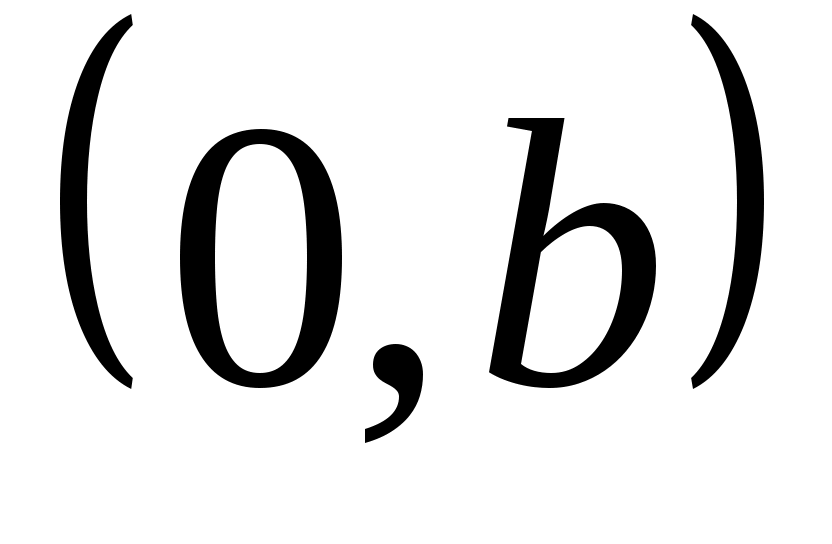 оси у; по этой причине ось у называют мнимой осью. На рис. 1 указаны изображения некоторых комплексных чисел.
оси у; по этой причине ось у называют мнимой осью. На рис. 1 указаны изображения некоторых комплексных чисел.
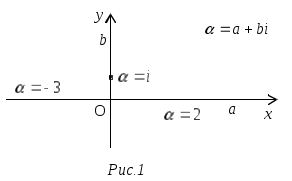
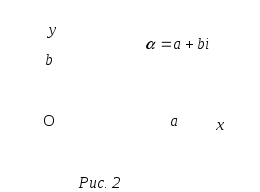
Наряду с изображением комплексных чисел точками плоскости применяется и другой способ изображения – с помощью векторов плоскости. Числу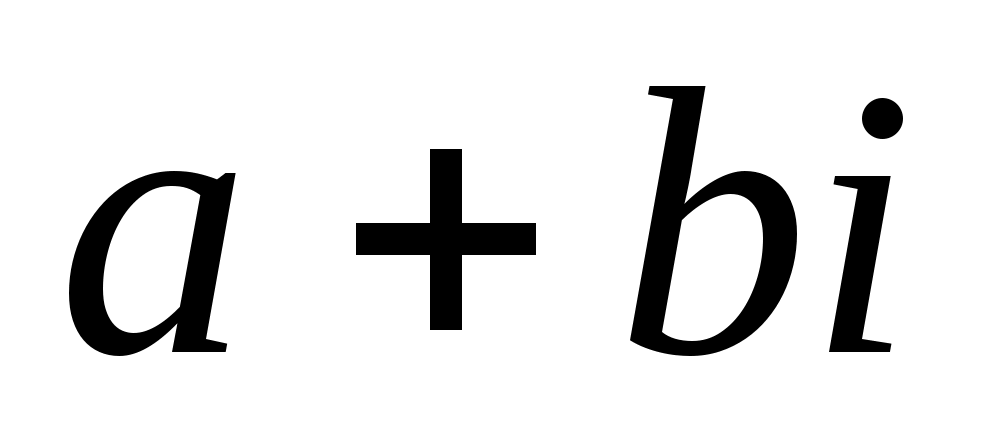 сопоставляется радиус-вектор точки
сопоставляется радиус-вектор точки  (Рис.2). «Точечный» и «векторный» способы изображения комплексных чисел применяются одинаково часто.
(Рис.2). «Точечный» и «векторный» способы изображения комплексных чисел применяются одинаково часто.
Изображение комплексных чисел с помощью векторов имеет то преимущество, что оно хорошо «увязано» с операцией сложения комплексных чисел. Пусть числам
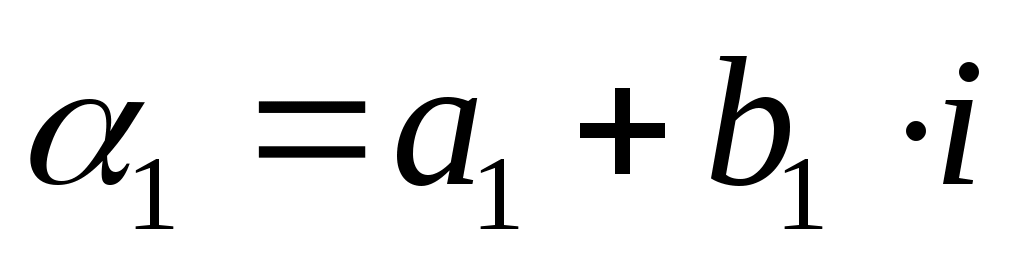 ,
, 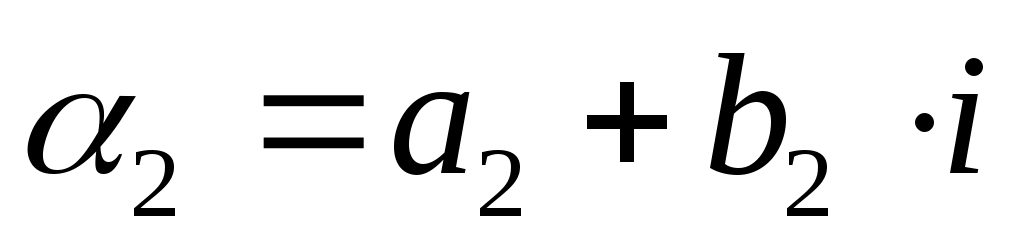 соответствуют векторы
соответствуют векторы 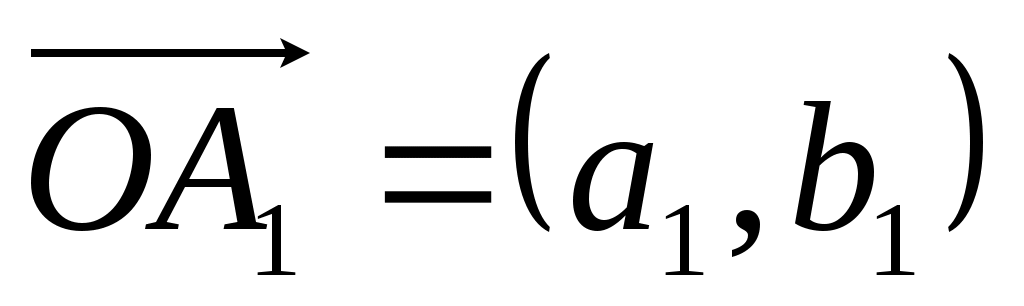 ,
, 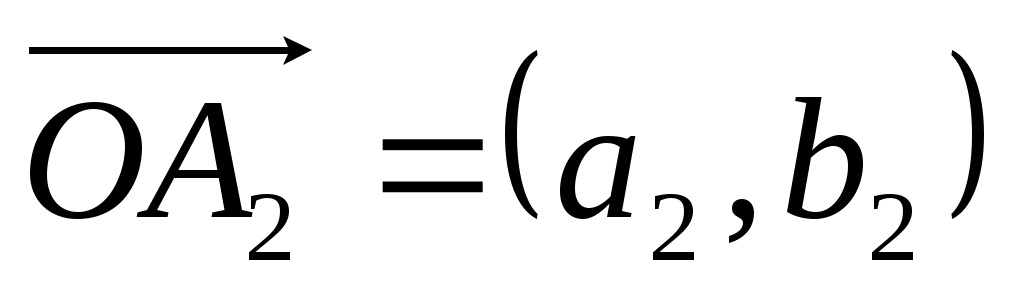 . Тогда числу
. Тогда числу 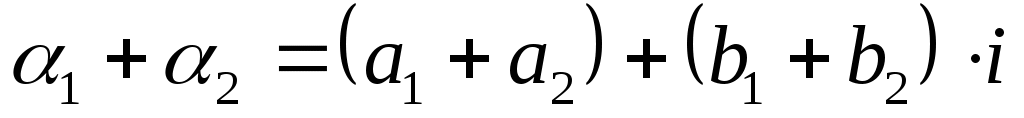 соответствует вектор с координатами
соответствует вектор с координатами 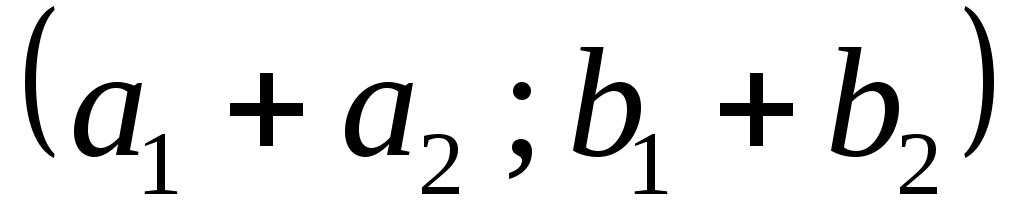 , т.е. вектор
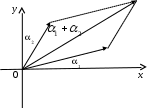
, т.е. вектор 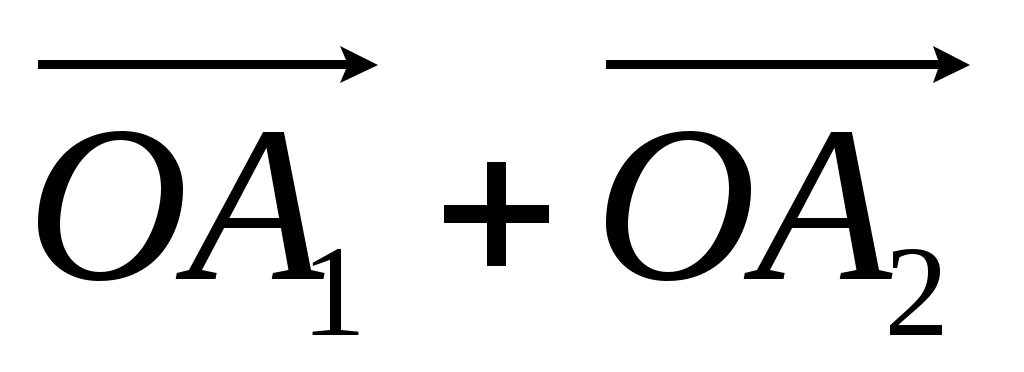 . Таким образом, сложение комплексных чисел геометрически сводится к сложению соответствующих векторов. Напомним, что сложение векторов осуществляется по правилу параллелограмма (рис. 3).
. Таким образом, сложение комплексных чисел геометрически сводится к сложению соответствующих векторов. Напомним, что сложение векторов осуществляется по правилу параллелограмма (рис. 3).
у
х
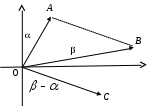
Рис. 3 Рис. 4
Поскольку сложение комплексных чисел сводится к сложению векторов, это же должно быть верно и по отношению к вычитанию. Если вектор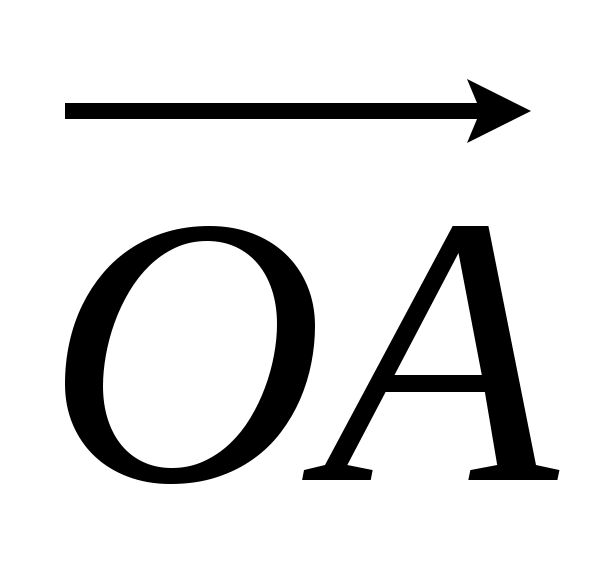 изображает комплексное число
изображает комплексное число  , а вектор
, а вектор 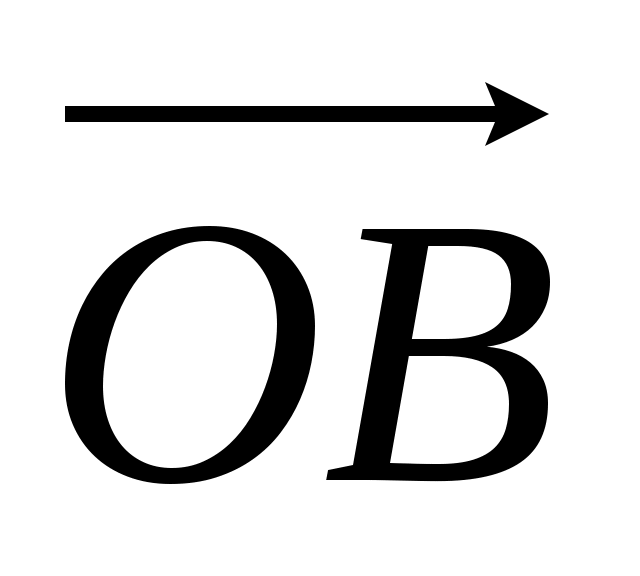 - число
- число 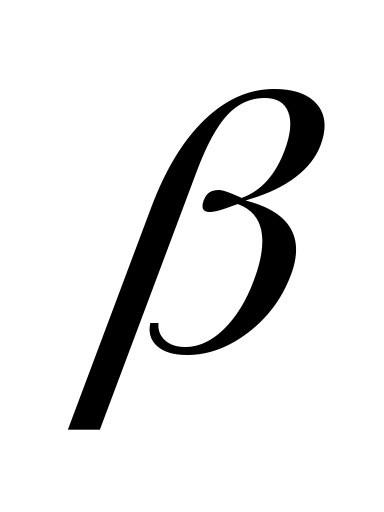 , то вектор
, то вектор 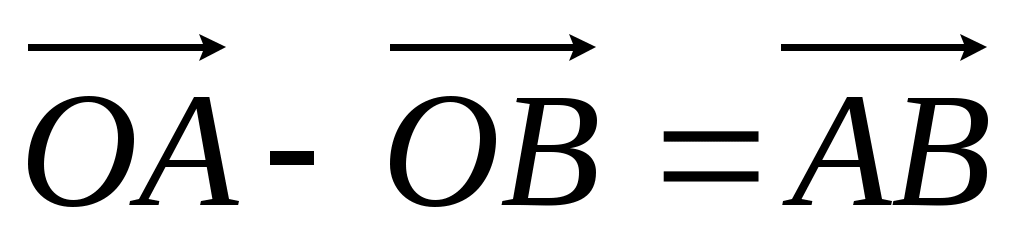 является изображением числа
является изображением числа 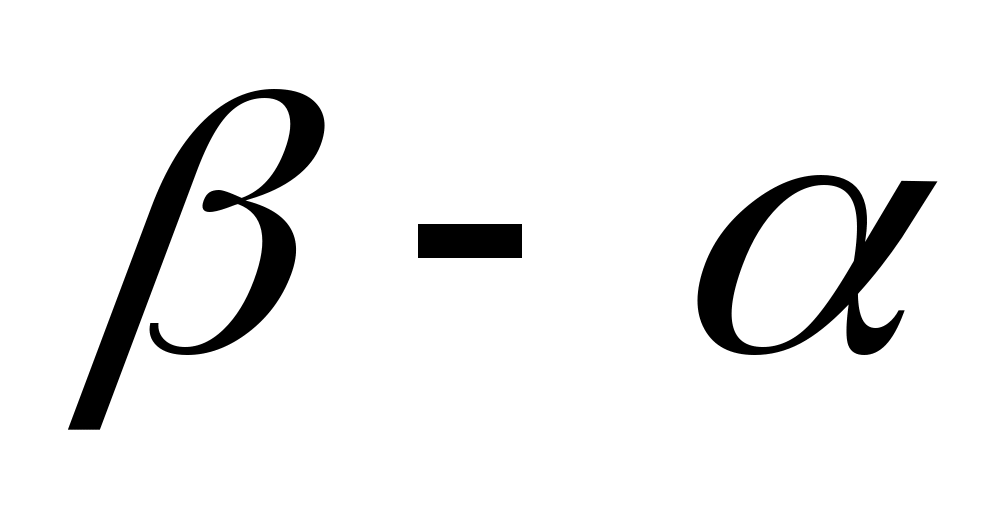 . Разумеется, чтобы получить точку, изображающую число
. Разумеется, чтобы получить точку, изображающую число 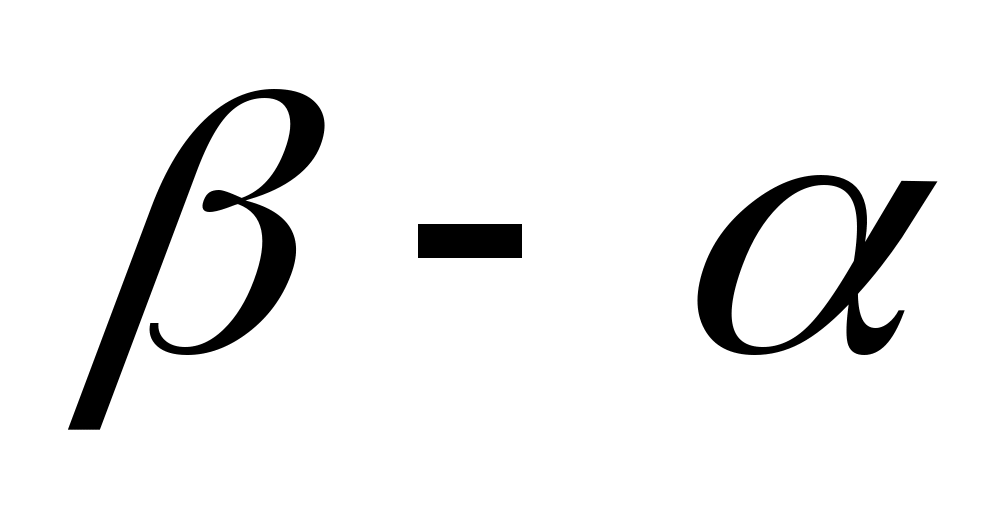 , этот вектор нужно отложить от начала координат (точка С на рис. 4).
, этот вектор нужно отложить от начала координат (точка С на рис. 4).
1.2 Тригонометрическая форма комплексного числа и
ее применение.
1.2.1. Модуль и аргумент комплексного числа.
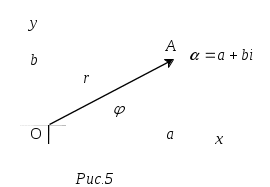
Комплексное число в прямоугольной декартовой системе координат
в прямоугольной декартовой системе координат
хОу изображается либо точкой А с абсциссой а и ординатой b, либо радиус-вектором этой точки . Длина вектора
. Длина вектора  называется модулемкомплексного числа и обозначается символом
называется модулемкомплексного числа и обозначается символом  :
:
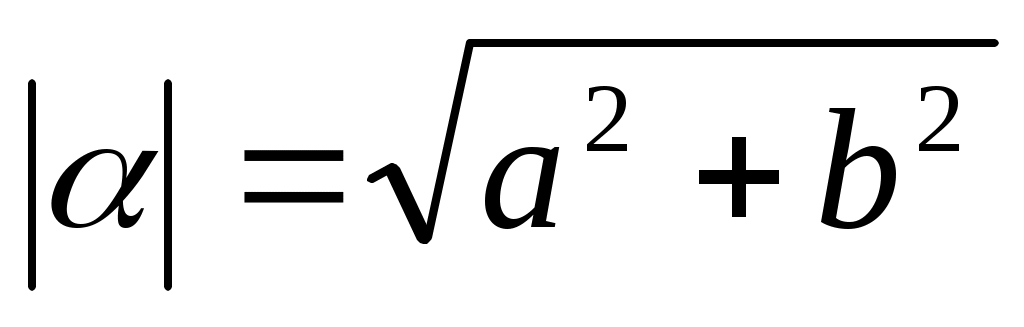 (1)
(1)
Угол , образованный вектором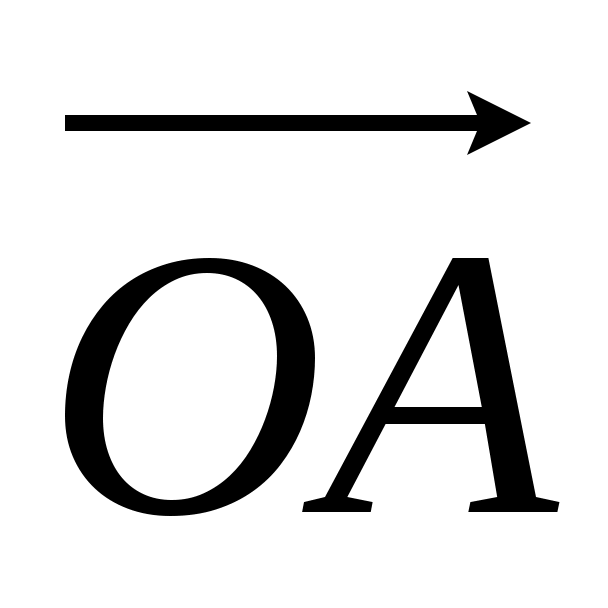 с положительным направлением оси Ох, называется аргументом числа и обозначается
с положительным направлением оси Ох, называется аргументом числа и обозначается 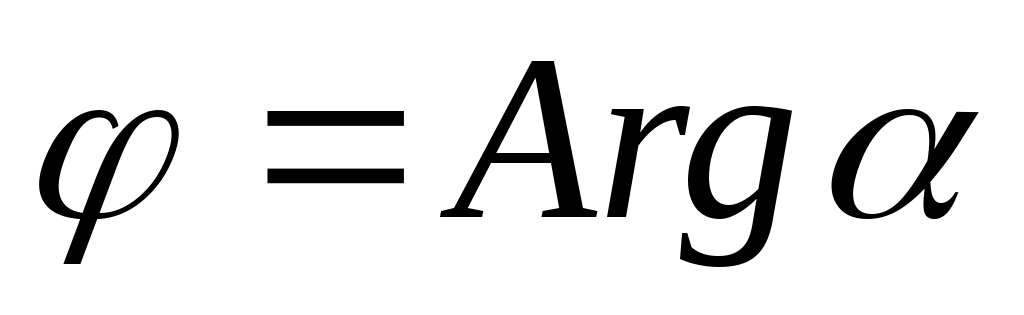 . Связь между аргументом комплексного числа и его действительной и мнимой частями выражается формулами
. Связь между аргументом комплексного числа и его действительной и мнимой частями выражается формулами
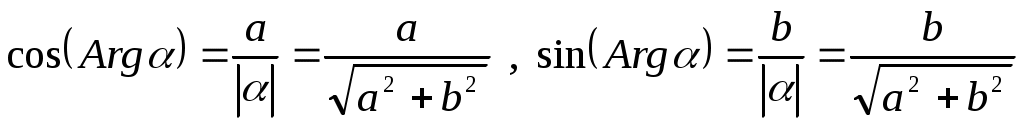 (2)
(2)
или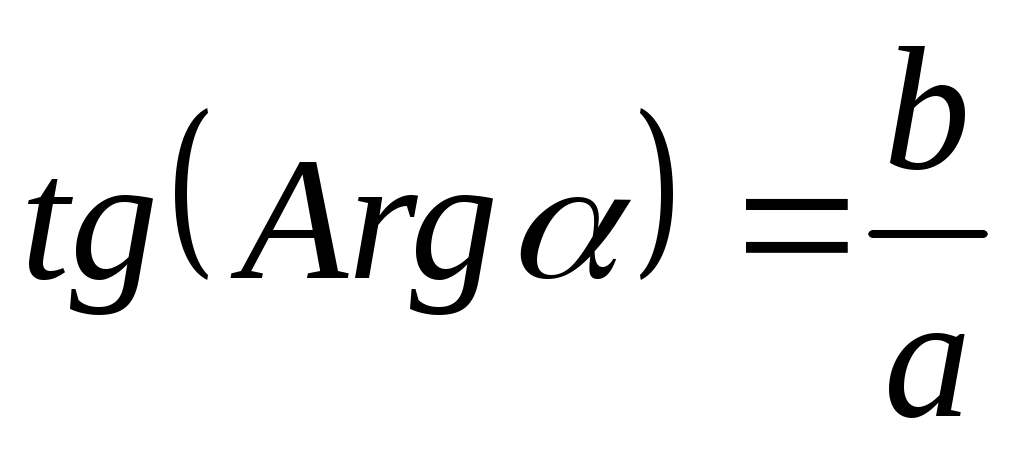 . (3)
. (3)
Формулы (2) и (3) позволяют для заданного комплексного числа находить модуль и аргумент. Обратно, если заданы модуль
находить модуль и аргумент. Обратно, если заданы модуль  и аргумент
и аргумент 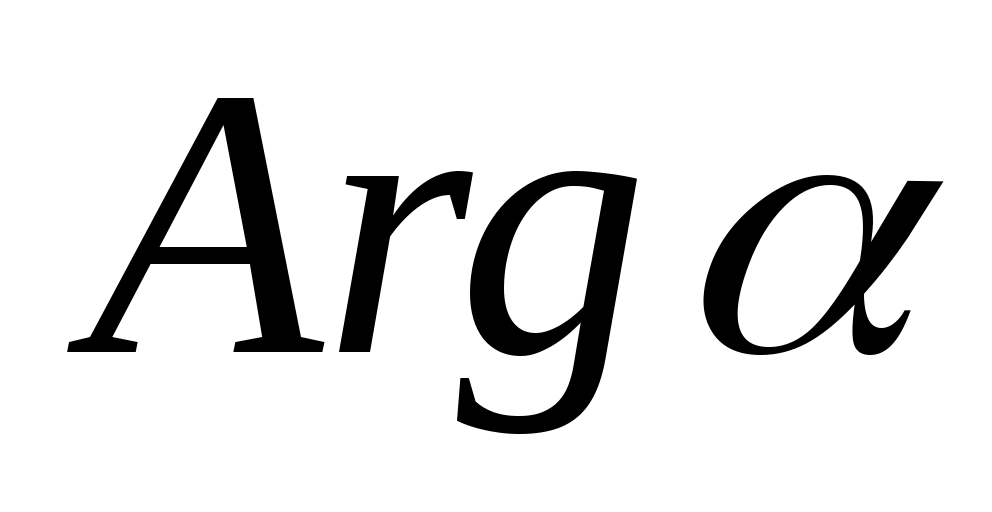 комплексного числа , то число
комплексного числа , то число  находится с помощью равенств:
находится с помощью равенств:
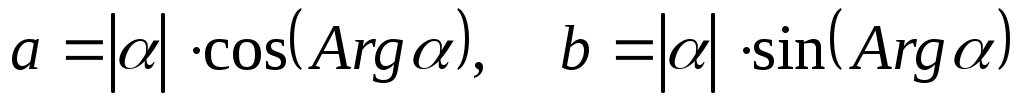 . (4)
. (4)
Аргумент комплексного числа определяется неоднозначно: если - аргумент числа , то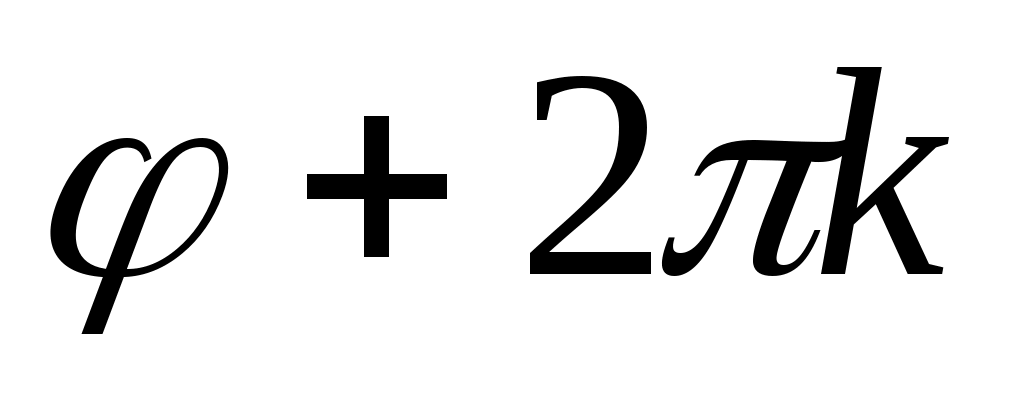 , где
, где 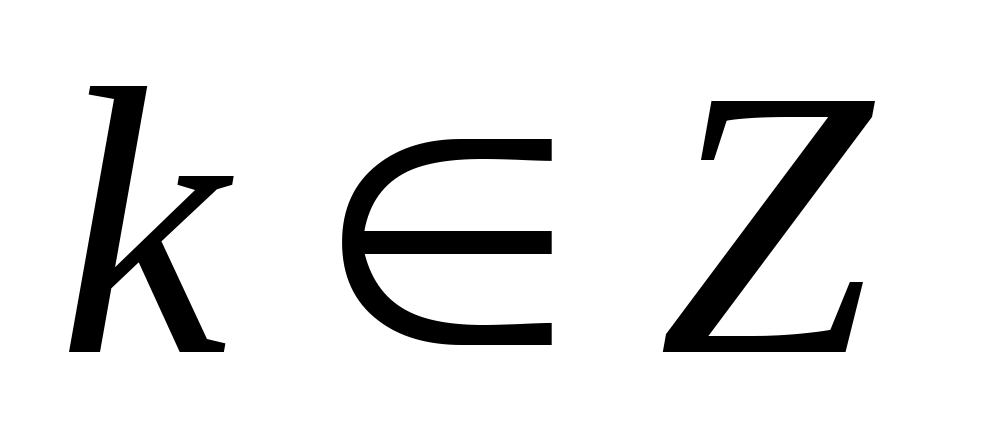 , - также аргумент этого числа. Для однозначности определения аргумента его выбирают в промежутке
, - также аргумент этого числа. Для однозначности определения аргумента его выбирают в промежутке 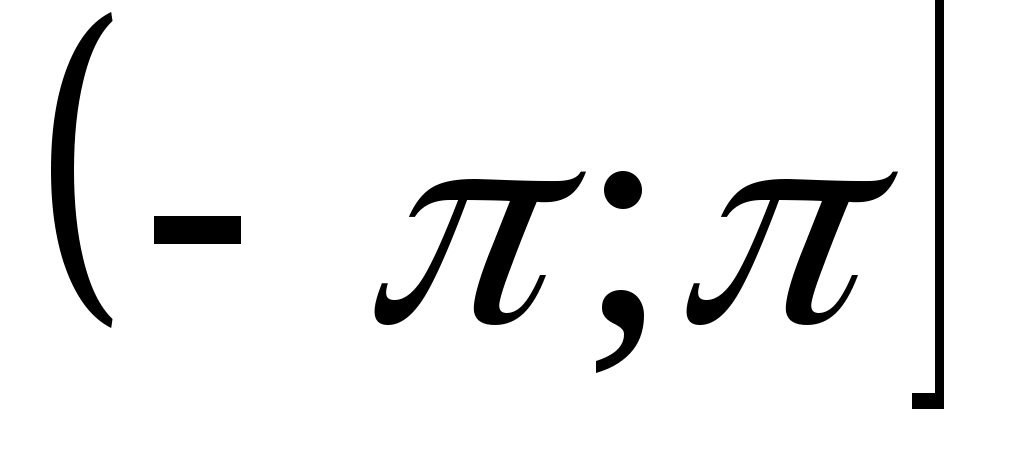 и называют главным значением аргумента. Главное значение аргумента обозначают
и называют главным значением аргумента. Главное значение аргумента обозначают 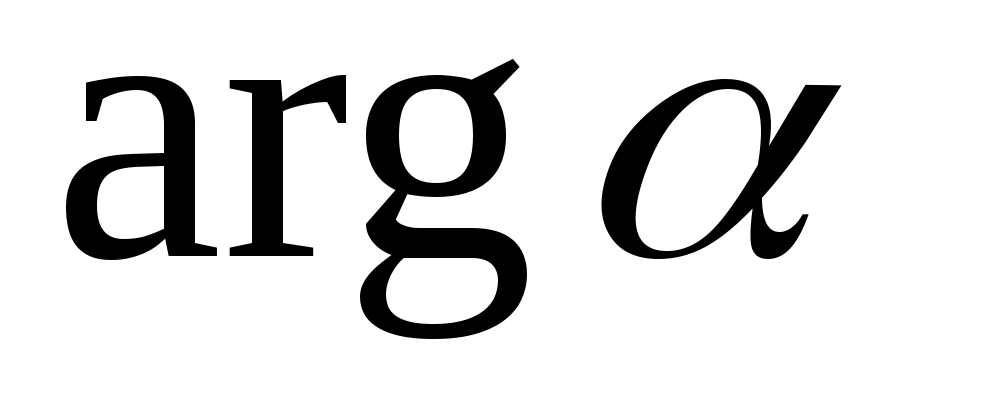 .
.
Так как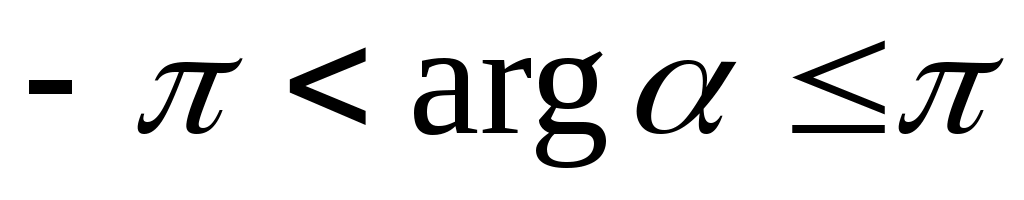
, то аргумент можно представить в виде
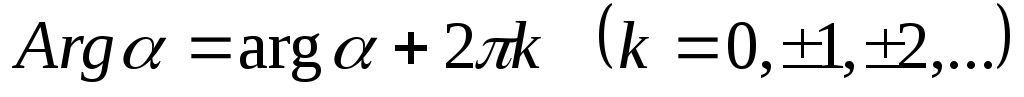 .
.
Пример 1. Найти модуль и аргумент комплексного числа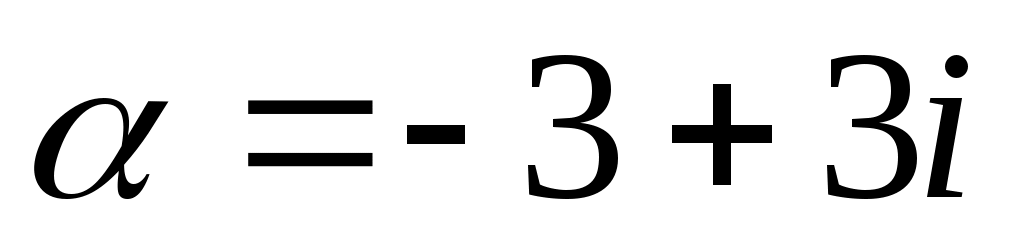 .
.
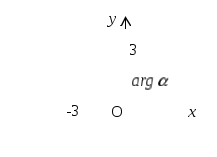
Используя формулу (1), находим модуль данного числа:
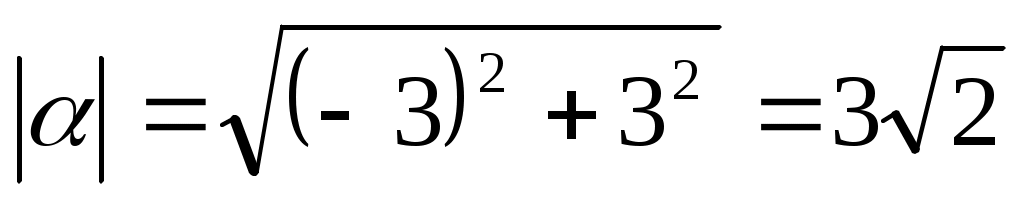 .
.
Далее, согласно формуле (2), получим
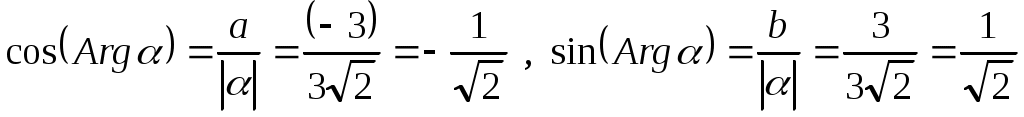
Так как точка, изображающая данное число, лежит во II четверти, то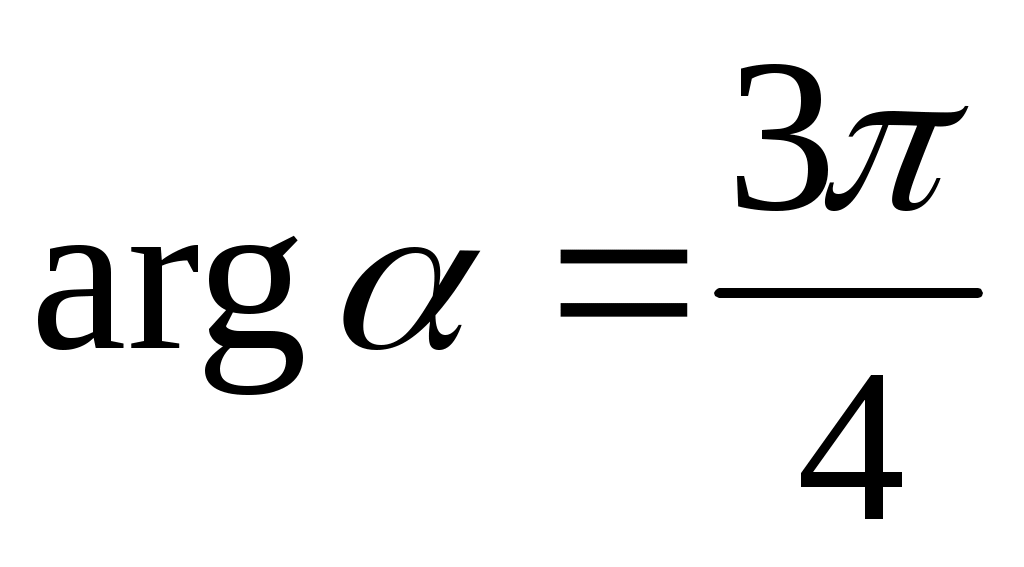 и, следовательно,
и, следовательно, 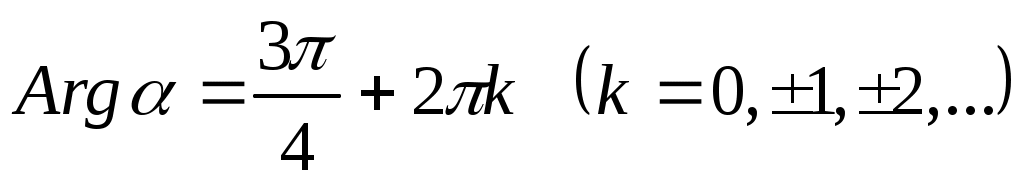 .
.
Для главного значения аргумента справедливы соотношения:
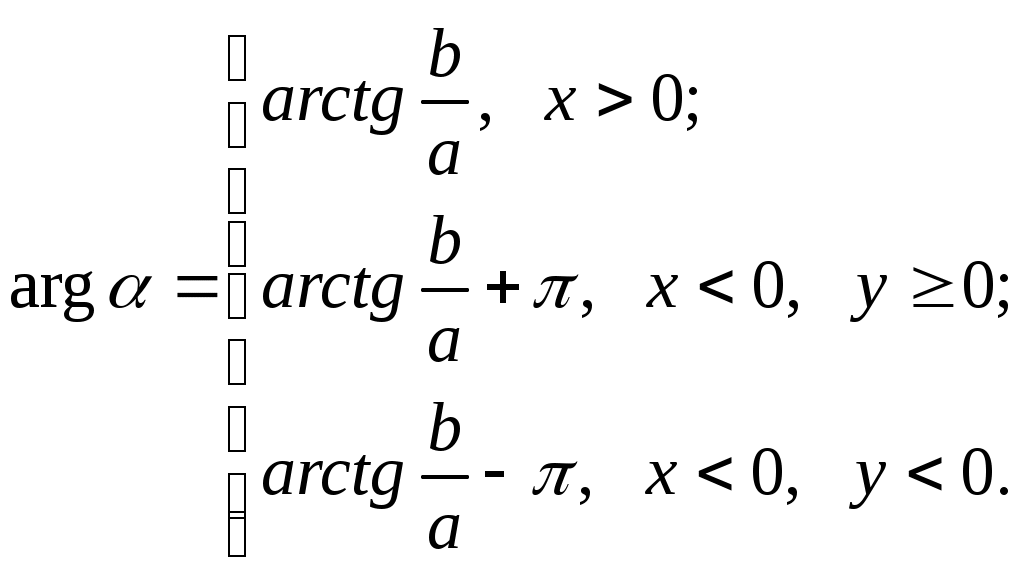
В самом деле, так как главное значение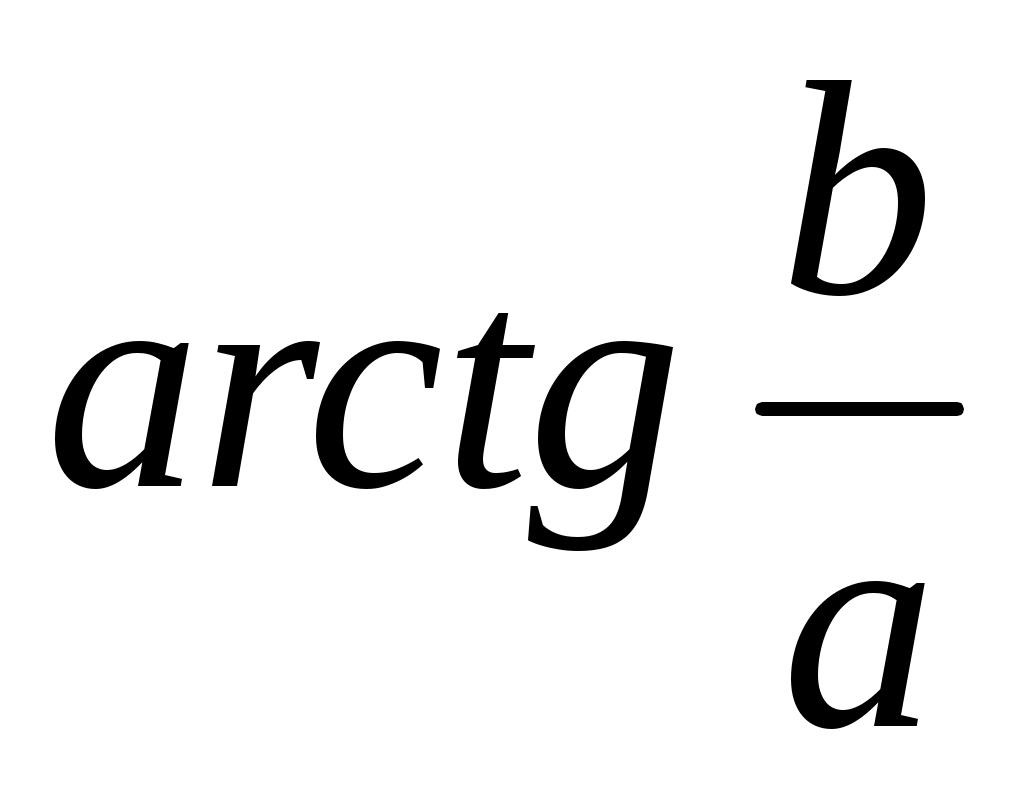 лежит между
лежит между 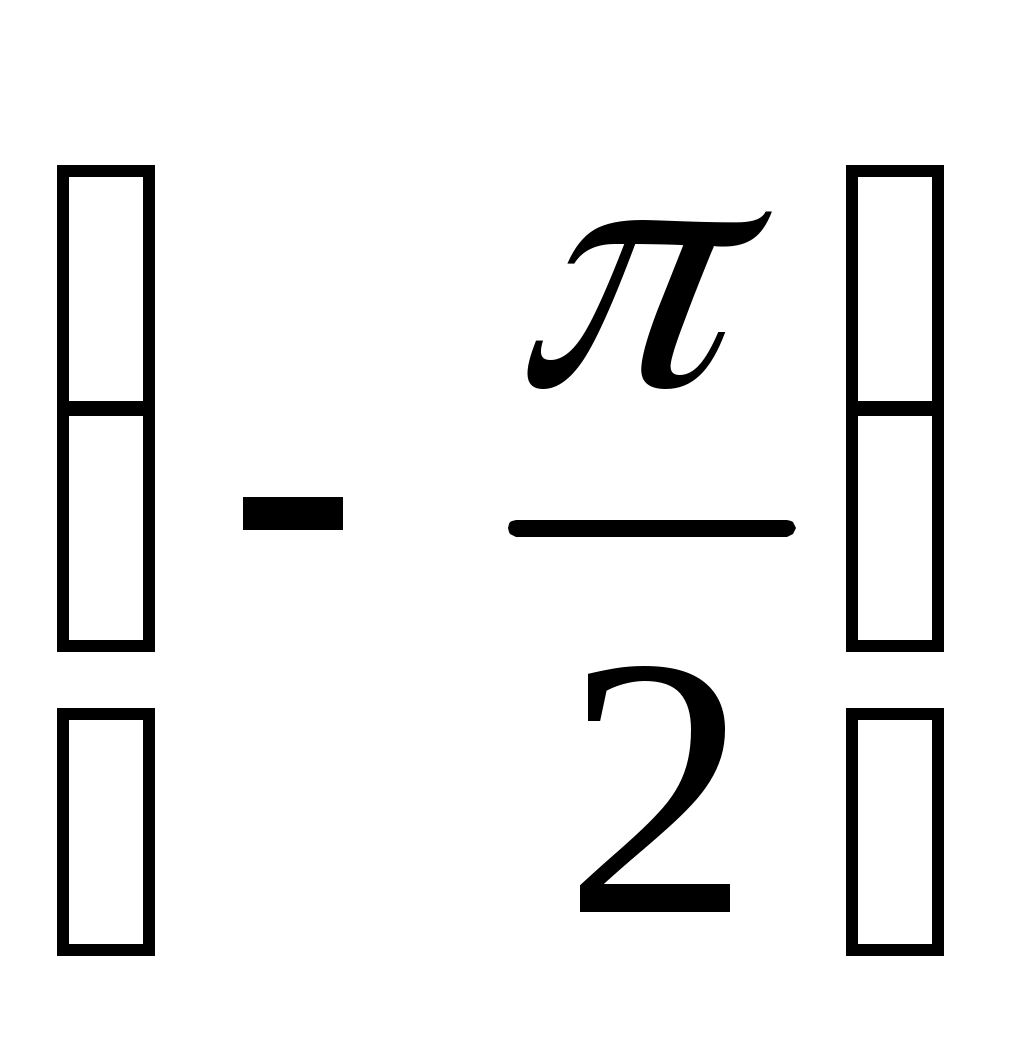 и
и 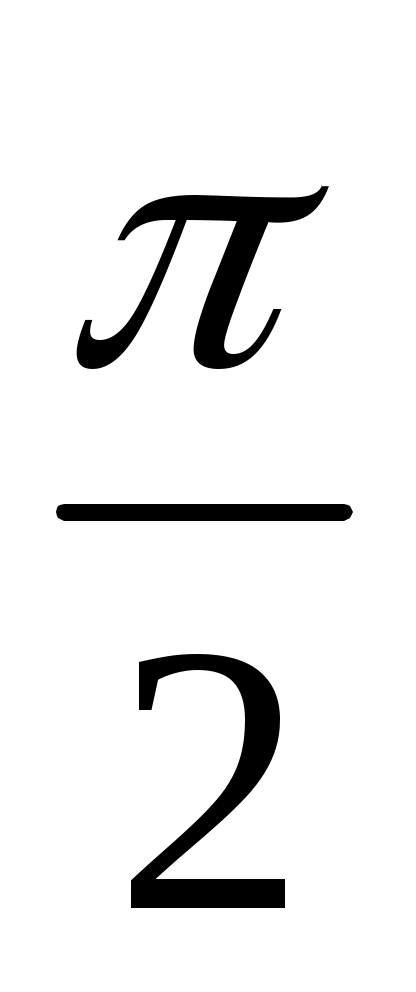 , то:
, то:
3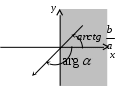 ) если точка лежит в III четверти
) если точка лежит в III четверти 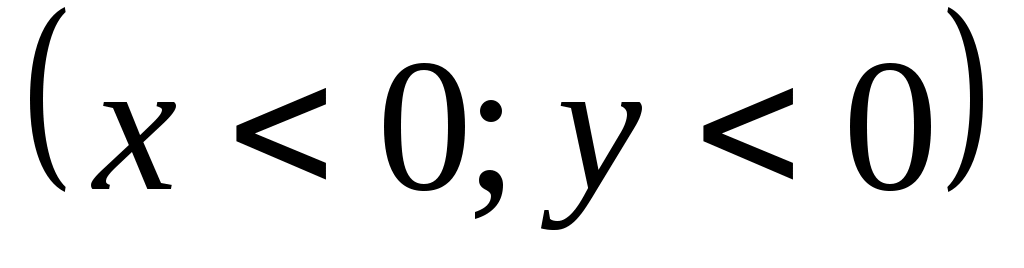 , то и
, то и 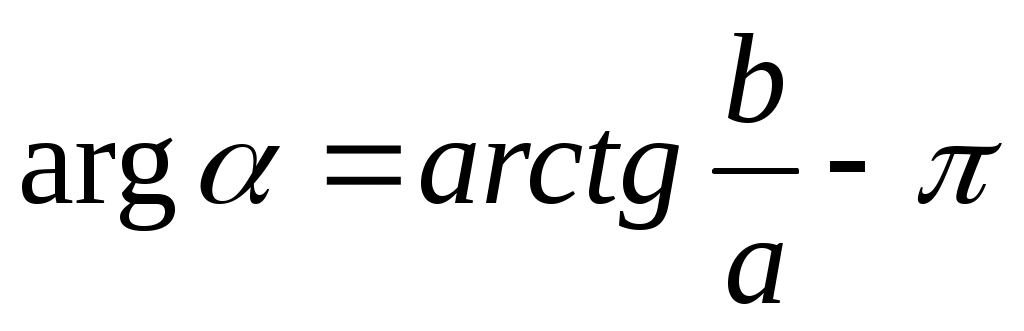 ;
;
Пример 2. Найти модуль и аргумент комплексного числа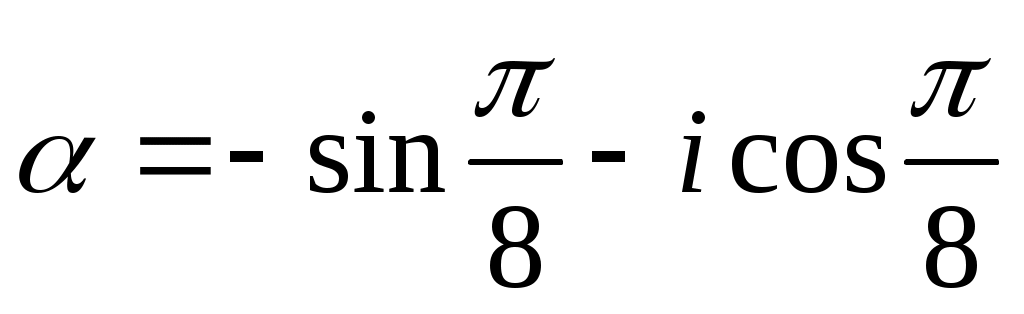 .
.
Решение. Вычислим модуль: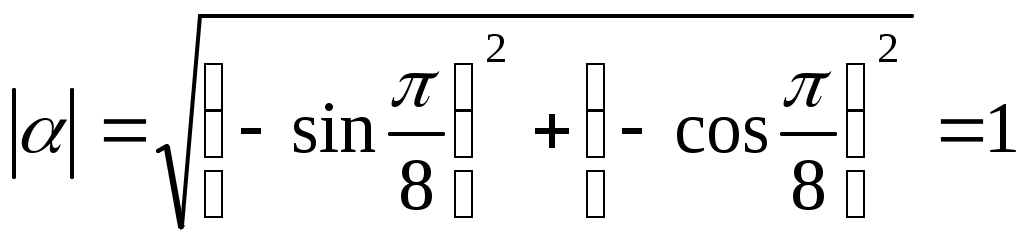
Итак, по определению,
Если
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами следует, что
1.
2.
3.
4.
Формула 1 определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула 2 означает, что при вычитании одного комплексного числа из другого, необходимо вычесть отдельно их действительные и мнимые части.
Формулу 3 можно получить путем умножения по правилам алгебры и замены
Чтобы получить формулу 4, необходимо предварительно числитель и знаменатель умножить на
Сформулируем основные свойства операции сопряжения:
1)
2)
3)
; 6)
Упражнение 2. Доказать свойства 1-5 операции сопряжения.
1.1.4 Геометрическое изображение комплексных чисел. Комплексная плоскость.
Если для изображения действительных чисел используются точки числовой прямой, то изображениями комплексных чисел служат точки координатной плоскости.
Введем на плоскости прямоугольную декартову систему координат с осями х и у. Тогда каждому комплексному числу
При таком способе изображения комплексных чисел любому действительному числу, т.е. числу вида

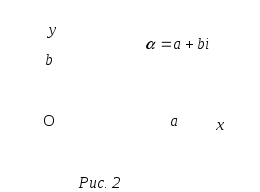
Наряду с изображением комплексных чисел точками плоскости применяется и другой способ изображения – с помощью векторов плоскости. Числу
Изображение комплексных чисел с помощью векторов имеет то преимущество, что оно хорошо «увязано» с операцией сложения комплексных чисел. Пусть числам

у
х

Рис. 3 Рис. 4
Поскольку сложение комплексных чисел сводится к сложению векторов, это же должно быть верно и по отношению к вычитанию. Если вектор
1.2 Тригонометрическая форма комплексного числа и
ее применение.
1.2.1. Модуль и аргумент комплексного числа.

Комплексное число
хОу изображается либо точкой А с абсциссой а и ординатой b, либо радиус-вектором этой точки
Угол , образованный вектором
или
Формулы (2) и (3) позволяют для заданного комплексного числа
Аргумент комплексного числа определяется неоднозначно: если - аргумент числа , то
Так как
, то аргумент можно представить в виде
Пример 1. Найти модуль и аргумент комплексного числа
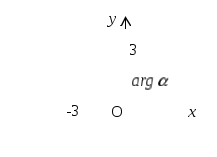
Используя формулу (1), находим модуль данного числа:
Далее, согласно формуле (2), получим
Так как точка, изображающая данное число, лежит во II четверти, то
Для главного значения аргумента справедливы соотношения:
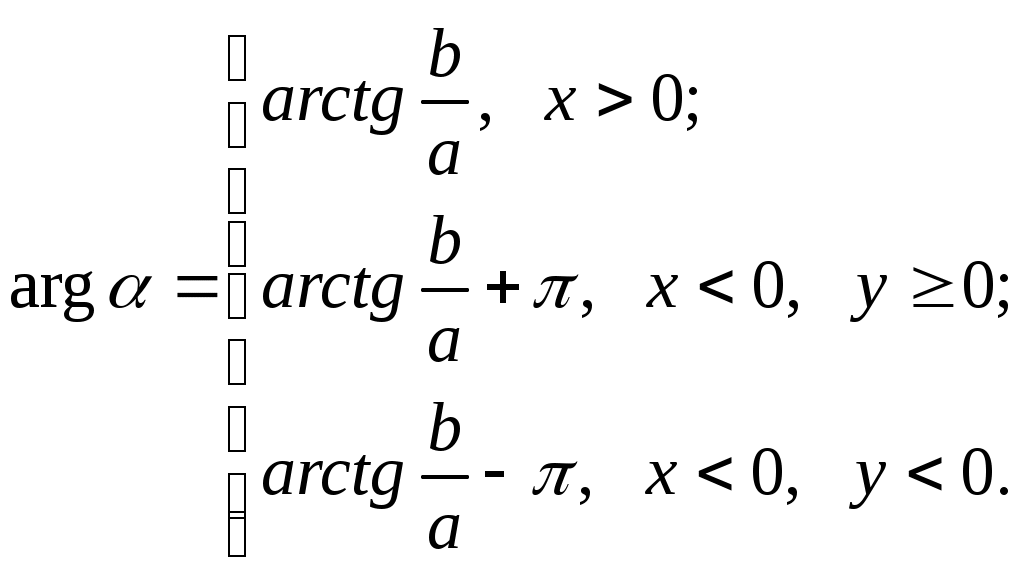
В самом деле, так как главное значение
-
е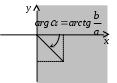 сли точка лежит в I или IV четверти
сли точка лежит в I или IV четверти 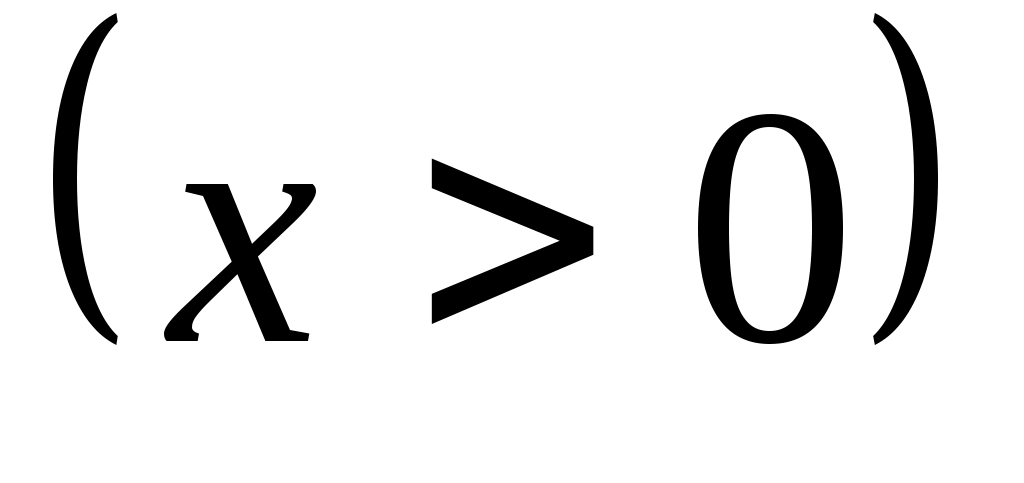 , то и
, то и 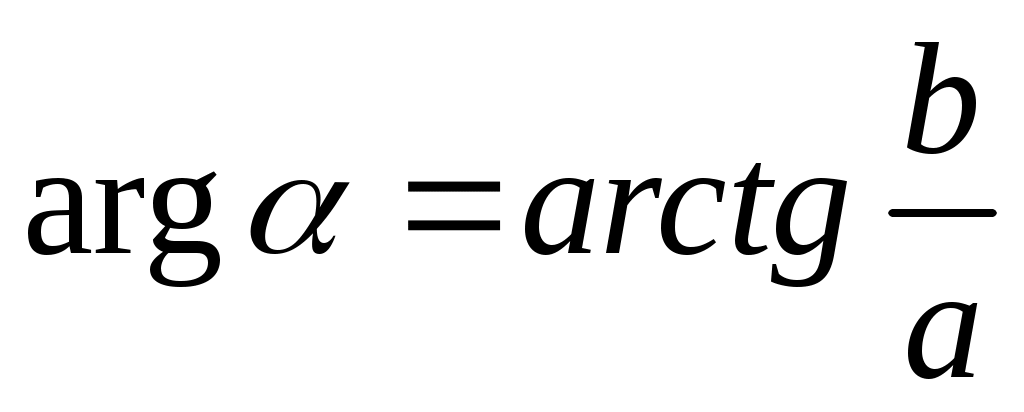 ;
;
-
е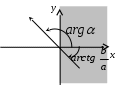 сли точка лежит в II четверти
сли точка лежит в II четверти 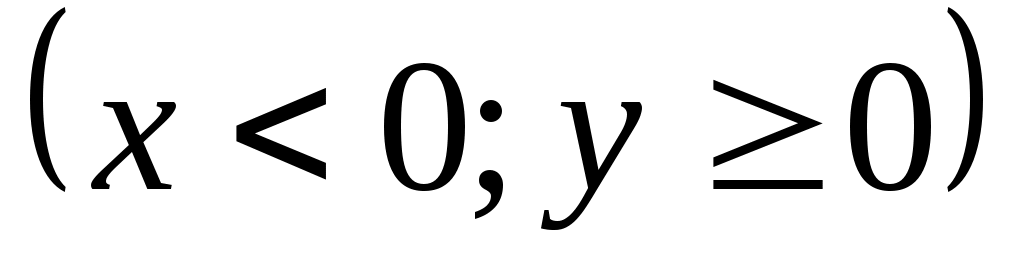 , то и
, то и 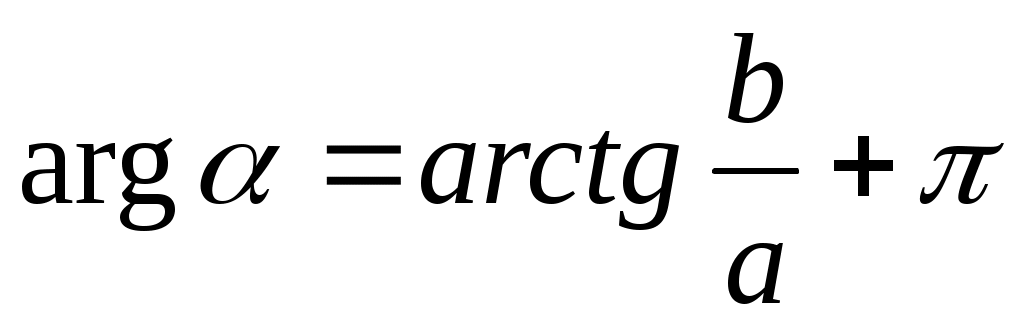 ;
;
3
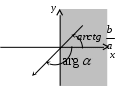 ) если точка лежит в III четверти
) если точка лежит в III четверти Пример 2. Найти модуль и аргумент комплексного числа
Решение. Вычислим модуль: