Добавлен: 26.10.2023
Просмотров: 152
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
техническому заданию исходное непрерывное сообщение представляет собой стационарный гауссовский случайный процесс с нулевым матожиданием, мощность и функция корреляции которого заданы в таблице с исходными данными.
представляет собой стационарный гауссовский случайный процесс с нулевым матожиданием, мощность и функция корреляции которого заданы в таблице с исходными данными.
Во временной и спектральной областях стационарный случайный процесс определяется функцией корреляции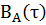 и спектром плотности мощности
и спектром плотности мощности 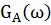 , где
, где 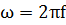 . Эти характеристики связанны между собой парой преобразований Винера –Хинчина:
. Эти характеристики связанны между собой парой преобразований Винера –Хинчина:
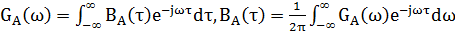
2.1 Интервал корреляции исходного сообщения
Интервал корреляции – промежуток времени между сечениями случайного процесса, в пределах которого наблюдается их корреляция.
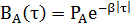
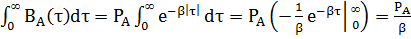
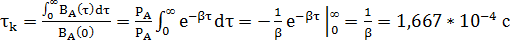
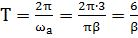
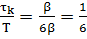
Т.к.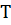 в 6 раз больше
в 6 раз больше 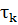 частотное заполнение можно не учитывать.
частотное заполнение можно не учитывать.
узкополосный гауссовский цифровой канал
2.2 Спектр плотности мощности
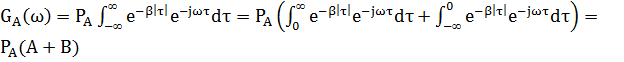
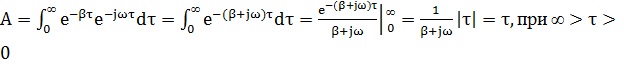
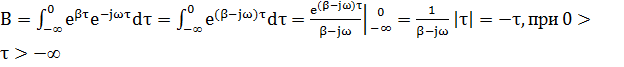
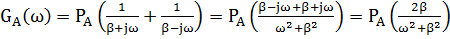
2.3 Начальная энергетическая ширина спектра сообщения
Ширина энергетического спектра – полоса частот, в пределах которой заключена основная доля энергии случайного процесса.
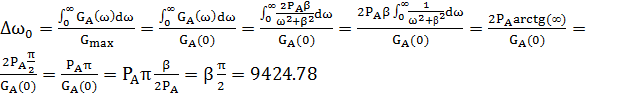
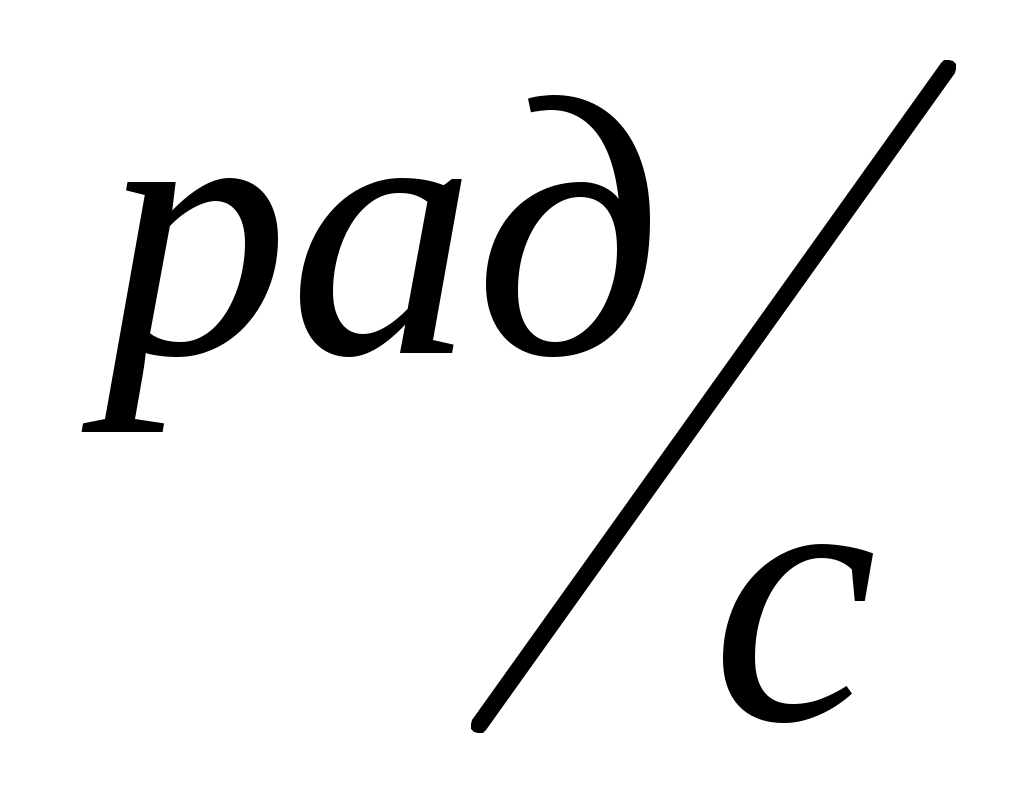
2.4 Графики функции корреляции и спектра плотности мощности
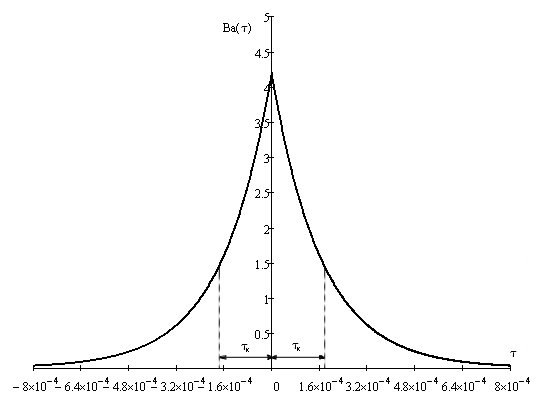
Рис. 2 – функция корреляции
На рис.2 пунктиром обозначено значение интервала корреляции, отложенное в обе стороны от нуля по оси времени.
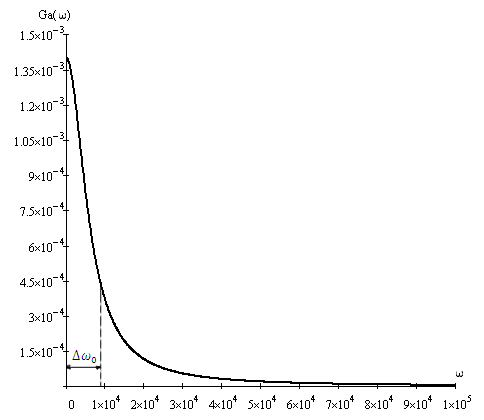
Рис.3 – энергетический спектр.
На рис.3пунктиром обозначена величина ширины энергетического спектра.
Задание № 3
Будем считать, что сообщение воздействует на идеальный ФНЧ с единичным коэффициентом передачи и полосой пропускания, равной начальной ширине энергетического спектра сообщения.
3.1 Средняямощность отклика ИФНЧ
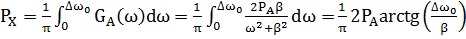
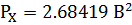
3.2 Средняяквадратическая погрешность фильтрации сообщения
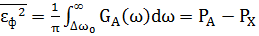
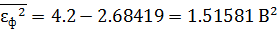
3.3 Интервал и частота дискретизации
По условию курсовой работы фильтр нижних частот идеален, и пропускает частоты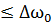 . Учтём также, что частота дискретизации равна удвоенной верхней частоте. Тогда в соответствии с теоремой Котельникова имеем
. Учтём также, что частота дискретизации равна удвоенной верхней частоте. Тогда в соответствии с теоремой Котельникова имеем
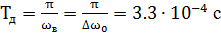
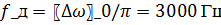
3.4 Сигналы и спектры на входе и выходе дискретизатора
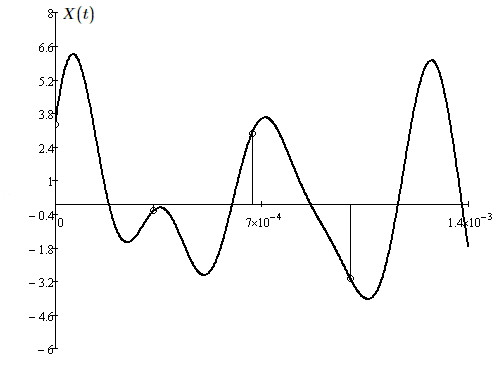
Рис. 4 – сигнал на входе и выходе дискретизатора.
На рис. 5 вертикальными линиями с маркерами обозначен сигнал на выходе дискретизатора.
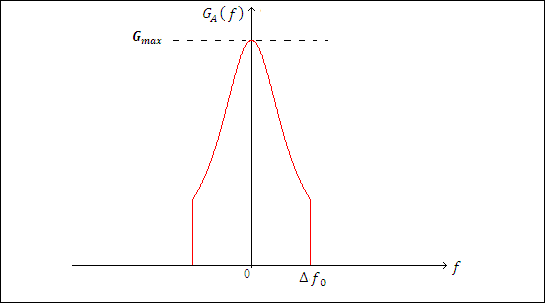
Рис.5 – спектр сигнала на входе дискретизатора АЦП.
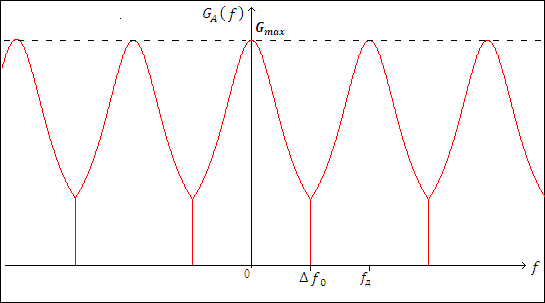
Рис.6 – спектр сигнала на выходе дискретизатора АЦП
Задание № 4
Далее последовательность дискретных отчетов на выходе дискретизатора квантуется по уровню равномерной шкалой квантования.Гауссовский случайный процесс с вероятностью 0.997 находится в диапазоне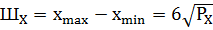
4.1 Интервал квантования
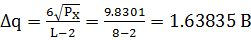
4.2 Пороги квантования
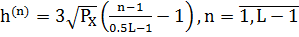
4.3 Уровни квантования
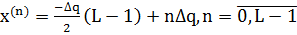
4.4 Средняяквадратическая погрешность квантования
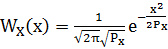 - ФПВ гауссовского случайного процесса в любой момент времени.
- ФПВ гауссовского случайного процесса в любой момент времени.
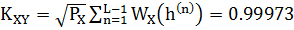
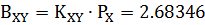
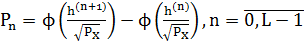
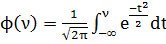
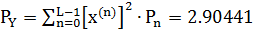
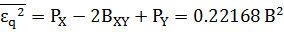
4.5 Характеристика квантования
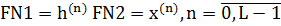
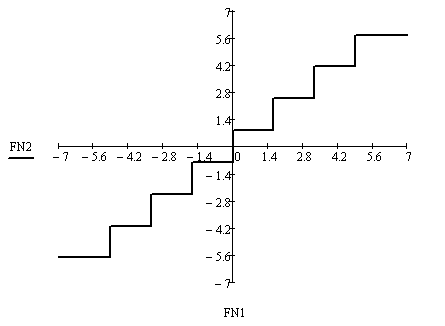
Рис. 7 – характеристика квантователя
Задание №5
5.1 Функция распределения вероятностей квантованного сигнала
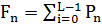
5.2 Закон распределения вероятностей квантованного сигнала
Закон распределения вероятностей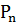 был найден в пункте 4.4
был найден в пункте 4.4
5.3 Энтропия L – ичного дискретного источника
Во временной и спектральной областях стационарный случайный процесс определяется функцией корреляции
2.1 Интервал корреляции исходного сообщения
Интервал корреляции – промежуток времени между сечениями случайного процесса, в пределах которого наблюдается их корреляция.
Т.к.
узкополосный гауссовский цифровой канал
2.2 Спектр плотности мощности
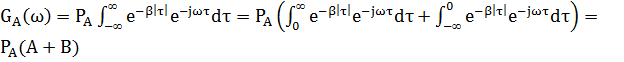
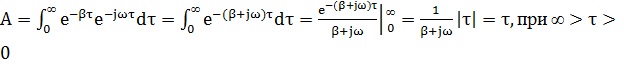
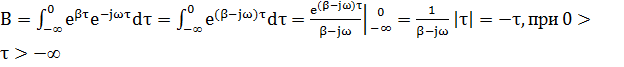
2.3 Начальная энергетическая ширина спектра сообщения
Ширина энергетического спектра – полоса частот, в пределах которой заключена основная доля энергии случайного процесса.
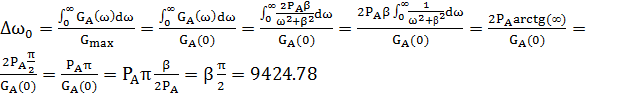
2.4 Графики функции корреляции и спектра плотности мощности

Рис. 2 – функция корреляции
На рис.2 пунктиром обозначено значение интервала корреляции, отложенное в обе стороны от нуля по оси времени.

Рис.3 – энергетический спектр.
На рис.3пунктиром обозначена величина ширины энергетического спектра.
Задание № 3
Будем считать, что сообщение воздействует на идеальный ФНЧ с единичным коэффициентом передачи и полосой пропускания, равной начальной ширине энергетического спектра сообщения.
3.1 Средняямощность отклика ИФНЧ
3.2 Средняяквадратическая погрешность фильтрации сообщения
3.3 Интервал и частота дискретизации
По условию курсовой работы фильтр нижних частот идеален, и пропускает частоты
3.4 Сигналы и спектры на входе и выходе дискретизатора

Рис. 4 – сигнал на входе и выходе дискретизатора.
На рис. 5 вертикальными линиями с маркерами обозначен сигнал на выходе дискретизатора.

Рис.5 – спектр сигнала на входе дискретизатора АЦП.

Рис.6 – спектр сигнала на выходе дискретизатора АЦП
Задание № 4
Далее последовательность дискретных отчетов на выходе дискретизатора квантуется по уровню равномерной шкалой квантования.Гауссовский случайный процесс с вероятностью 0.997 находится в диапазоне
4.1 Интервал квантования
4.2 Пороги квантования
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| | | -4.91505 | -3.2767 | -1.63835 | 0 | 1.63835 | 3.2767 | 4.91505 | |
4.3 Уровни квантования
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | -5.73422 | -4.09587 | -2.45752 | -0.81917 | 0.81917 | 2.45752 | 4.09587 | 5.73422 |
4.4 Средняяквадратическая погрешность квантования
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | -4.91505 | -3.2767 | -1.63835 | 0 | 1.63835 | 3.2767 | 4.91505 |
| | 0.00271 | 0.03295 | 0.14769 | 0.2435 | 0.14769 | 0.03295 | 0.00271 |
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | 0.00132 | 0.0214 | 0.13591 | 0.34134 | 0.34134 | 0.13591 | 0.0214 | 0.00132 |
4.5 Характеристика квантования

Рис. 7 – характеристика квантователя
Задание №5
5.1 Функция распределения вероятностей квантованного сигнала
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | 0.00132 | 0.02272 | 0.15862 | 0.49997 | 0.84131 | 0.97722 | 0.99862 | 0.99994 |
5.2 Закон распределения вероятностей квантованного сигнала
Закон распределения вероятностей
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | 0.00132 | 0.0214 | 0.13591 | 0.34134 | 0.34134 | 0.13591 | 0.0214 | 0.00132 |
5.3 Энтропия L – ичного дискретного источника