Кафедра «Экономика и менеджмент»РЕФЕРАТпо дисциплине «Математическое обеспечение финансовых решений»на тему «Формирование оптимального портфеля ценных бумаг по Марковицу, рыночная эффективная граница и факторы, ее определяющие»Студент: Воскресенский Владимир АлексеевичНаправление: ЭкономикаГруппа № СМЛС22-М-БА01ВВЕДЕНИЕОсновная задача, которую необходимо решить при формировании портфеля ценных бумаг, — распределение инвестором определенной денежной суммы по различным альтернативным вложениям (например, акции, облигации, наличные деньги и др.) так, чтобы наилучшим образом достичь своих целей. Портфель ценных бумаг — совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, выступающая как целостный объект управления, имеющая своей целью улучшать условия инвестирования, придав данной совокупности такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятой ценой бумаги и возможны только при их комбинации.Тип портфеля — это его инвестиционная характеристика, основанная на соотношении дохода и риска. В первую очередь инвестор стремится к получению максимального дохода за счет выигрыша от благоприятного изменения курса акций, дивидендов, получения твердых процентов и т.д. С другой стороны, любое вложение капитала связано не только с ожиданием получения дохода, но и с постоянной опасностью проигрыша, а значит, в оптимизационных за­дачах по выбору портфеля ценных бумаг необходимо учитывать риск. В принципе для создания портфеля ценных бумаг достаточно инвестировать деньги в какой-либо один вид финансовых активов. Но современная экономическая практика показывает, что такой однородный по содержанию портфель (не диверсифицированный) встречается очень редко. Гораздо более распространенной формой является так называемый диверсифицированный портфель, т.е. портфель с самыми разнообразными ценными бумагами. Портфель, состоящий из акций разноплановых компаний, обеспечивает стабильность получения положительного результата. Нынешнее состояние финансового рынка заставляет быстро и адекватно реагировать на его изменения, поэтому роль управления инвестиционным портфелем резко возрастает и заключается в нахождении той грани между ликвидностью, доходностью и рискованностью, которая позволила бы выбрать оптимальную структуру портфеля. Этой цели служат различные модели выбора оптимального портфеля.

---

ПОНЯТИЕ ОПТИМАЛЬНОГО ПОРТФЕЛЯОптимальный портфель – набор активов, позволяющих инвестору добиться тех финансовых целей, которые он преследует. Оптимальный портфель – субъективное понятие: тот набор, который будет подходить одному инвестору, для другого окажется непригодным. Состав активов зависит от допустимого уровня риска и инвестиционной стратегии. Оптимальный портфель – 1) эффективный портфель, которому инвестор отдает предпочтение, поскольку параметры риска/вознаграждения этого портфеля приближены к функции полезности инвестора; 2) портфель, максимизирующий предпочтения инвестора в отношении доходности и риска. Предполагает умеренное сочетание доходности и риска. Формирование инвестиционного портфеля оптимального вида состоит, как правило, из акций крупный и проверенных акционерных обществ, характеризующихся стабильно-высокими показателями деятельности в течение последних 5 лет. Допускается приобретение ценных бумаг, подверженных резкому движению курса, но при условии постоянного мониторинга. Приверженцами оптимального портфеля являются инвесторы, вкладывающие на 5-10 лет. Их основная цель – сохранить денежные средства от инфляции и небольшое стабильное приумножение капитала на 10-15% в год.ТЕОРИЯ ГАРРИ МАРКОВИЦАТеория формирования инвестиционного портфеля, предложенная нобелевским лауреатом по экономике Гарри Марковицем, является наиболее распространенной и популярной. Суть теории Марковица заключается в том, что диверсификация всегда дает инвестору преимущество (ученый это математически доказал). Кроме того, Марковиц выдвинул следующий тезис: риск инвестиционного портфеля зависит не только от того, какую долю занимает определенный актив, но и от взаимосвязей, существующих между всеми активами, входящими в портфель. Оптимален тот портфель, который включает в себя акции компаний, занимающихся разными видами деятельности, относящихся к разным отраслям и минимально между собой коррелирующих. Если есть возможность, лучше собрать портфель из разнородных инструментов: акций, облигаций, валютных пар. Исследования показали, что максимальное количество активов, которые могут быть включены в один портфель – 20. Если активов больше, эффективность портфеля уже не будет максимальной.

---

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах. Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях[3]. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык[4]. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.После проведённой Марковицем формализации, с математической точки зрения задача по формированию оптимального портфеля представляла собой задачу квадратической оптимизации при линейных ограничениях. Этот класс задач, является одним из наиболее изученных классов оптимизационных задач, для которых существует большое число эффективных алгоритмов. Для построения пространства возможных портфелей Марковиц предложил использовать класс активов, вектор их средних ожидаемых доходностей и матрицу ковариаций. На основе этих данных строится множество возможных портфелей с различными соотношениями доходность-риск. Так как в основе анализа лежат два критерия, менеджер выбирает портфели:

• 
  Либо поиском эффективных, или неулучшаемых решений. В этом случае любое другое решение, лучше найденных по одному параметру обязательно будет хуже по другому.
  
• 
  Либо выбирая главный критерий (например, доходность должна быть не ниже определённой величины) остальные используя лишь в качестве критериальных ограничений.
  
• 
  Либо задавая некий суперкритерий, который является суперпозицией указанных двух (например, их функцией).
  

Выбор оптимального портфеля.Инвестор должен нарисовать свои кривые безразличия на одном рисунке с эффективным множеством, а затем приступить к выбору портфеля, расположенного на кривой безразличия, находящейся выше и левее остальных. Этот портфель будет соответствовать точке, в которой кривая касается эффективного множества. Как это видно из рис. 2, таким портфелем является портфель О* на кривой безразличия I2. Несомненно, что инвестор предпочел бы портфель, находящийся на кривой I3 , но такого достижимого портфеля просто не существует. Желание находиться на какой-то конкретной кривой не может быть реализовано, если данная кривая нигде не пересекает множество достижимости. Что касается кривой I1, то существует несколько портфелей, которые может выбрать инвестор (например, О). Однако рисунок показывает, что портфель О* является наилучшим из этих портфелей, так как он находится на кривой безразличия, расположенной выше и левее. Рисунок 3 показывает, что инвестор с высокой степенью избегания риска выберет портфель, рас­положенный близко к точке Е. Рисунок 4 показывает, что инвестор с низкой степенью избегания риска выберет портфель, расположенный близко к точке S. Кривые безразличия для инвестора, избегающего риск, выпуклы и имеют положительный наклон. Эффективное множество в общем случае вогнуто и имеет положительный наклон, т.е. отрезок, соединяющий любые две точки эффективного множества, лежит ниже данного множества. Это свойство эффективных множеств является очень важным, так как оно означает, что существует только одна точка касания эффективного множества и кривых безразличия.

---

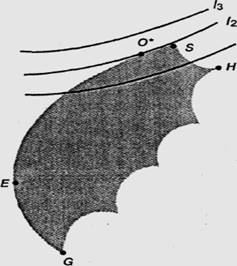
Рис. 4.Выбор портфеля инвестором с низкой степенью избегания риска.Г. Марковитц разработал математическую модель формирования оптимального портфеля, за которую ему была присуждена Нобелевская премия в области экономики в 1990г., и методы построения портфелей при определенных критериях. Подход Марковица начинается с предположения, что инвестор в настоящий момент времени имеет конкретную сумму денег для инвестирования. Эти деньги будут инвестированы на определенный промежуток времени – период владения. Если задать желаемый для инвестора уровень доходности портфеля, то можно поставить задачу выбора такой структуры портфеля, которая при заданном уровне доходности приводила бы к минимальному риску. Сложность практического внедрения данной модели обусловлена тем, что в тот период времени использование теории вероятностей в финансовой теории не воспринималось теоретиками-экономистами и практиками. Вместе с тем затруднение внедрения модели Г. Марковица обусловливалось неразвитостью вычислительной техники и сложностью алгоритмов расчета. Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную, т.е. доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. Для упрощения модель Марковица полагает, что доходы по альтернативам инвестирования распределены нормально. По модели Марковица определяются показатели, характеризующие объект инвестиций и риск, что позволяет сравнить между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций. Метод оптимального портфеля по Марковитцу решает следующие вопросы:

• 
  Дает ответ на вопрос, оптимален ли инвестиционный портфель организации.
  
• 
  Рассчитывает эффективную границу для сравнения множественных портфельных распределений.
  
• 
  Позволяет определить портфель, который обеспечивает наиболее подходящую комбинацию риска и доходности для организации.
  
• 
  Отслеживает текущий портфель, что дает возможность корректировать его состав с точки зрения оптимизации риска и доходности.
  
• 
  Позволяет отбирать активы для коротких продаж, распределяя получаемые средства оптимальным образом среди оставшихся активов.
  

---

В качестве масштаба ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.Пусть формируется портфель из nценных бумаг. Ожидаемое значение дохода по i-й ценной бумаге (Ei ) рассчитывается как среднеарифметическое из отдельных возможных доходов Ri с весами Pij , приписанным им вероятностями наступления:nEi = S Ri * Pijj =1где сумма Pij = 1;n– задает количество оценок дохода по каждой ценной бумаге.Для измерения риска служат показатели рассеивания, поэтому чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Таким образом, риск выражается отклонением (причем более низких) значений доходов от наиболее вероятного значения. Мерой рассеивания является среднеквадратичное отклонение si и, чем больше это значение, тем больше риск:nEi = Ö ( S Pij (Rij – Ei )2 )j =1В модели Марковица для измерения риска вместо среднеквадратичного отклонения используется дисперсия Di , равная квадрату si , так как этот показатель имеет преимущества по технике расчетов. Инвестора, желающего оптимально вложить капитал, интересует не столько сравнение отдельных видов ценных бумаг между собой, сколько сравнение всевозможных портфелей, так как это позволяет использовать эффект рассеивания риска, т.е. определяется ожидаемое значение дохода и дисперсия портфеля. Ожидаемое значение дохода Е портфеля ценных бумаг определяется как сумма наиболее вероятных доходов Ei различных ценных бумаг n. При этом доходы взвешиваются с относительными долями Xj (i= 1…n), соответствующими вложениям капитала в каждую облигацию или акцию:nE = S Xi * Eii =1модели Марковица для измерения риска вместо среднеквадратичного отклонения используется дисперсия Di , равная квадрату si , так как этот показатель имеет преимущества по технике расчетов. Инвестора, желающего оптимально вложить капитал, интересует не столько сравнение отдельных видов ценных бумаг между собой, сколько сравнение всевозможных портфелей, так как это позволяет использовать эффект рассеивания риска, т.е. определяется ожидаемое значение дохода и дисперсия портфеля. Ожидаемое значение дохода Е портфеля ценных бумаг определяется как сумма наиболее вероятных доходов Ei различных ценных бумаг n. При этом доходы взвешиваются с относительными долями Xj (i= 1…n), соответствующими вложениям капитала в каждую облигацию или акцию:

---

Смотрите также файлы

• Лекарствоведение Тибета.docx

• Планконспект проведения занятий по дисциплине аварийноспасательные работы.docx

• Реферат по дисциплине Материаловедение На тему Ортопедические конструкции на основе благородных металлов. Показания к применению, характеристика, свойства, практическое применение..docx

• Билет 12 Задание 1 Охарактеризуйте особенности развития и воспитания детей раннего возраста (первый, второй, третий годы жизни). Раскройте задачи воспитания и обучения детей 23 лет.docx

• Причины дтп подразделяются на субъективные (зависящие от воли человека) и объективные (не зависящие от воли человека).docx