ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 28
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Экзаменационные вопросы
по предмету Математика
| курс 1 | 2 семестр | группы Ип1-21 |
-
Таблица производных. Производная сложной функции.
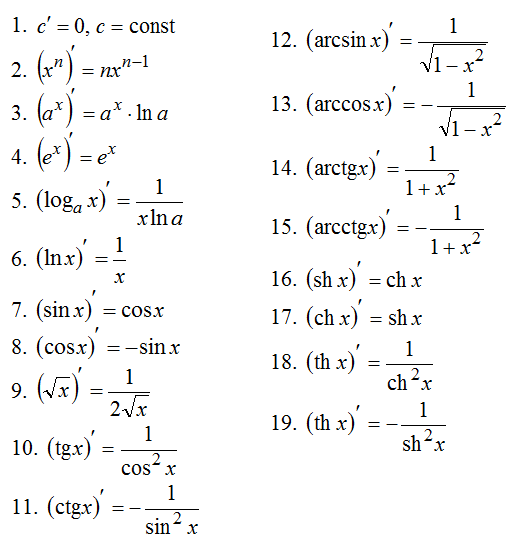
-
Нахождение промежутков монотонности функции. -
Нахождение экстремумов функции.
Точку х=х0 называют точкой мин. функции y=f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х0) выполняется неравенство f(x)> f(x0).
Точку х=х0 называют точкой max. функции y=f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х0) выполняется неравенство f(x)< f(x0).
Окрестность — это интервал, содержащий эту точку.
Теорема 1.
Если функция y=f(x) имеет экстремум в точке х=х0, то в этой точке производная функции либо равна 0, либо не существует.
Стационарные – точки, в которых производная функции равна 0.
Критические – точки, в которых производная равна нулю или не дифференцируется.
Теорема 2.
Пусть функция y=f(x) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х=х0.
-
если при переходе через стационарную точку х0 функции y=f(x) и её производная меняет знак с плюса на минус, то точка х0 – точка максимума. -
если при переходе через стационарную точку х0 функции y=f(x) и её производная меняет знак с минуса на плюс, то точка х0 – точка минимума. -
Если в этой точке существует такая окрестность, что в ней и слева и справа от точки х0 знаки производной одинаковы, то в точке х=х0 экстремума нет.
Алгоритм исследования непрерывной функции на монотонность и экстремумы.
-
Найти производную функции -
Найти стационарные и критические точки -
Отметить на числовой прямой и определить знаки производной на получившемся промежутке -
Опираясь на теоремы, сделать выводы о монотонности функции и о её точке экстремума.
! Если функция вида
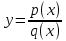 , отметить точки в которых q(x) =0. Данные точки не являются точками экстремума.
, отметить точки в которых q(x) =0. Данные точки не являются точками экстремума.-
Интервалы выпуклости и точки перегиба графика функции.
Кривая y=f(x) называется выпуклой вниз в промежутке х=(а,в) если она лежит выше касательной в любой точке этого промежутка.
Кривая y=f(x) называется выпуклой вверх в промежутке х=(а,в) если она лежит ниже касательной в любой точке этого промежутка.
Признак
Пусть f(x) имеет на интервале (а,в) вторую производную
Если f’’(x) <0, то функция выпукла вверх. Если f’’(x)>0, выпукла вниз.
Точка графика функции, разделяющая промежутки выпуклости противоположна направлению этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки второго порядка принадлежащие области определения функции.
Признак
Если при переходе через крит.т. второго порядка х0 вторая производная f’’(x) меняет знак, то график функции имеет точку перегиба (х0; f(x0))
-
Исследование функции и построение графика.
Найти
-
D(y) -
F’(x) -
Стационарные точки -
Промежутки возрастания и убывания -
Точки экстремума и значения функции в этих точках
Записать в виде таблицы, затем используя таблицу построить график функции.
| х | промежуток | точка максимума/минимума | промежуток |
| y’ | +/- | 0 | +/- |
| y |  | другое число |  |
| | | макс/мин | |
-
Дополнительные точки.
-
Наибольшее и наименьшее значения функции на отрезке и на интервале.
-
Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего и своего наименьшего значения -
Наибольшие и наименьшие значения функция может достигать, как и на концах отрезка, так и внутри него. -
Если набольшее/ наименьшее значение достигается внутри отрезка, то только в стационарной или критической точке
Алгоритм нахождения наибольшего и наименьшего значения
-
Найти первую производную функции -
Найти стационарные и критические точки -
Вычислить y=f(x) в точках, отобранных во 2 шаге и в точках, а и в, выбрать среди них наибольший и наименьший.
-
Первообразная. Правила нахождения первообразных.
Функция F(x) называется первообразной функции f(x) на некотором промежутке, если выполняется условие F(x)’= f(x).
Пусть F(x) и G(x) – первообразные соответствующих функций f(x) и g(x) на некотором промежутке
Тогда:
-
F(x) +- G(x) – является первообразной f(x) +- g(x). -
аF(x) является первообразной аf(x).
Интегрирование – операция нахождения первообразной данной функции.
-
Таблица первообразных.

-
Неопределенный интеграл и его свойства.
Если y=f(x) имеет на Х первообразную y=F(x), то множество функций y=F(x)+С, называются неопределённым интегралом от y=f(x) и обозначаются
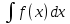
Где
 - знак интеграла, f(x) – подынтегральная функция.
- знак интеграла, f(x) – подынтегральная функция.-
Определенный интеграл и его свойства. Формула Ньютона-Лейбница. -
Площадь криволинейной трапеции и интеграл. Вычисление площадей фигур с помощью интегралов.
Геометрический смысл определённого интеграла:
Разность F(b) – F(a) называется интегралом от функции f(x) на отрезке [а;в] и обозначают так:

Если интегрируемая на отрезе [а;в] функция f(x)≥0, то определённый
 численно равна площади криволинейной трапеции ограниченной графиком функции y=f(x) с осью Ох и прямыми х=а и х=в.
численно равна площади криволинейной трапеции ограниченной графиком функции y=f(x) с осью Ох и прямыми х=а и х=в. 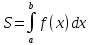
Если f(x)≤0 для х[а;в] , то
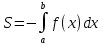 или
или 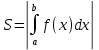
Свойства интегралов:
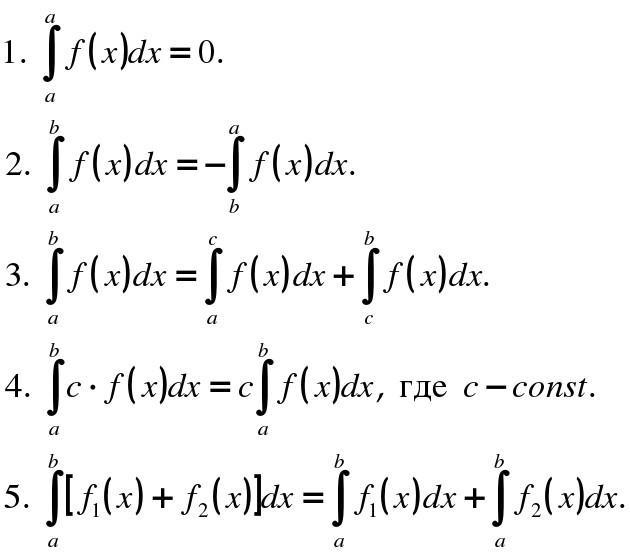
-
Призма: элементы, виды, свойства. -
Площадь боковой поверхности прямой призмы (с доказательством). -
Площадь боковой поверхности наклонной призмы (с доказательством).
Призма – это многогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях.
Элементы призмы:
Равные многоугольники – основания, а боковые стороны – боковые грани.
Отрезки соединяющие соответствующие вершины оснований называются боковыми рёбрами.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если в основание лежит n-угольник, то призма называется n-угольной.
Если боковые рёбра призмы перпендикулярны к основанию, то призма – прямая, если нет – наклонная.
В наклонной призме боковые грани – параллелограммы, в прямой – прямоугольники.
Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольник.
Теорема
Площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания:

Теорема:
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярному сечения на боковое ребро.
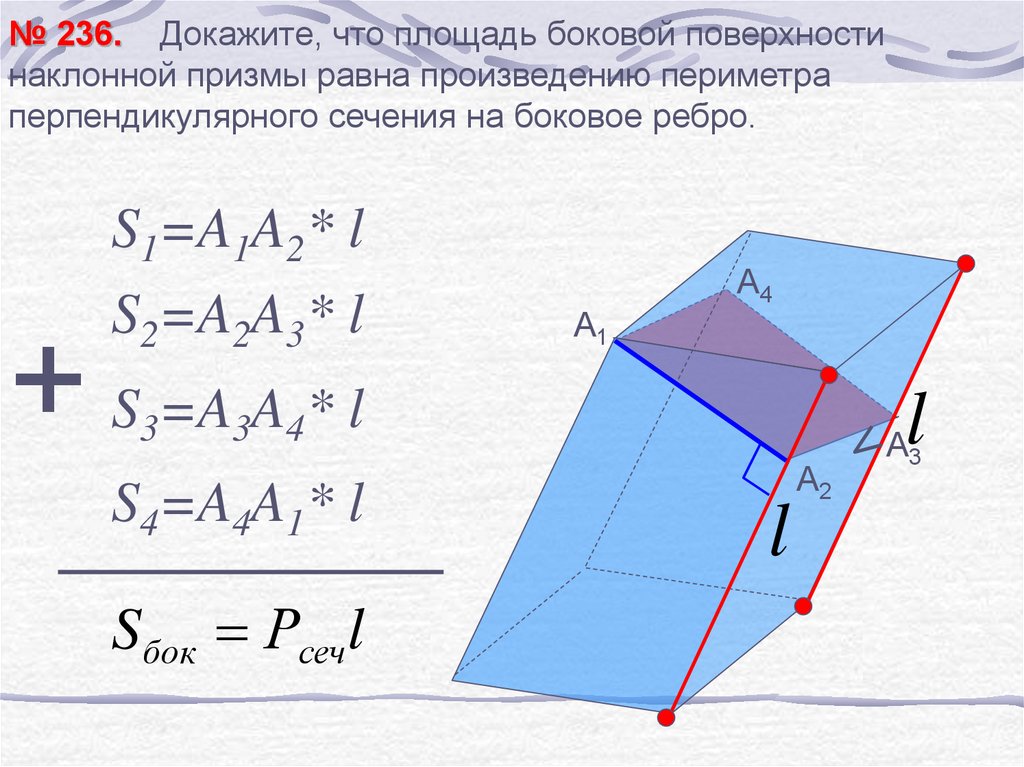
Сечение призмы плоскостью, проходящей через 2 боковых ребра не принадлежащих одной грани, называется диагональным.
Перпендикулярным сечением наклонной призмы называется её сечение плоскостью, перпендикулярной к боковым рёбрам и пересекающей их.
-
Параллелепипед, его виды и свойства. Куб.
Параллелепипед – поверхность, составленная из шести параллелограммов, или призма в основание которого лежит параллелограмм.
Если в основание прямого параллелепипеда прямоугольники, то параллелограмм прямоугольный.
Свойство 1.
Противоположные грани параллелепипеда параллельны и равны.
Свойство 2.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Параллелепипед называется прямоугольным если его боковые рёбра перпендикулярны к основанию, а основания – прямоугольники.
-
В прямом параллелепипеде все 6 граней – прямоугольники. -
Все двугранные углы прямоугольного параллелепипеда – прямые.
Длины трёх рёбер, имеющих общую вершину назовём измерениями прямоугольного параллелепипеда.
Куб — правильный многогранник, каждая грань которого представляет собой квадрат.
Диагональ куба со стороной а равна а
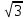
-
Свойство диагоналей прямоугольного параллелепипеда (с доказательством).
Теорема:
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений.
Доказательство:
AC1=AB2+AD2+AA12

-
Пирамида: элементы, виды, свойства.
Пирамида — многогранник, одна из граней которого — произвольный многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Апофема – высота боковой грани правильной пирамиды.
Пирамида правильная, если её основание – правильный многоугольник, а вершина проецируется в центр основания.
-
Площадь боковой поверхности правильной пирамиды (с доказательством).
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Главный зависимости для многоугольников, около которых можно описать окружность
| Многоугольник | Центр описанной окружности | Формулы |
| произвольный треугольник | точка пересечения серединных перпендикуляров | R=  ; ; 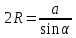 |
| р/б треугольник | точка пересечения серединных перпендикуляров находится на высоте проведённой к основанию | R=  ; ; 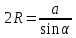 R= 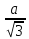 – р/с – р/с |
| прямоугольный треугольник | середина гипотенузы | R – половина гипотенузы |
| прямоугольник | точка пересечения диагоналей | R – половина диагонали |