ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2021
Просмотров: 6575
Скачиваний: 50
656
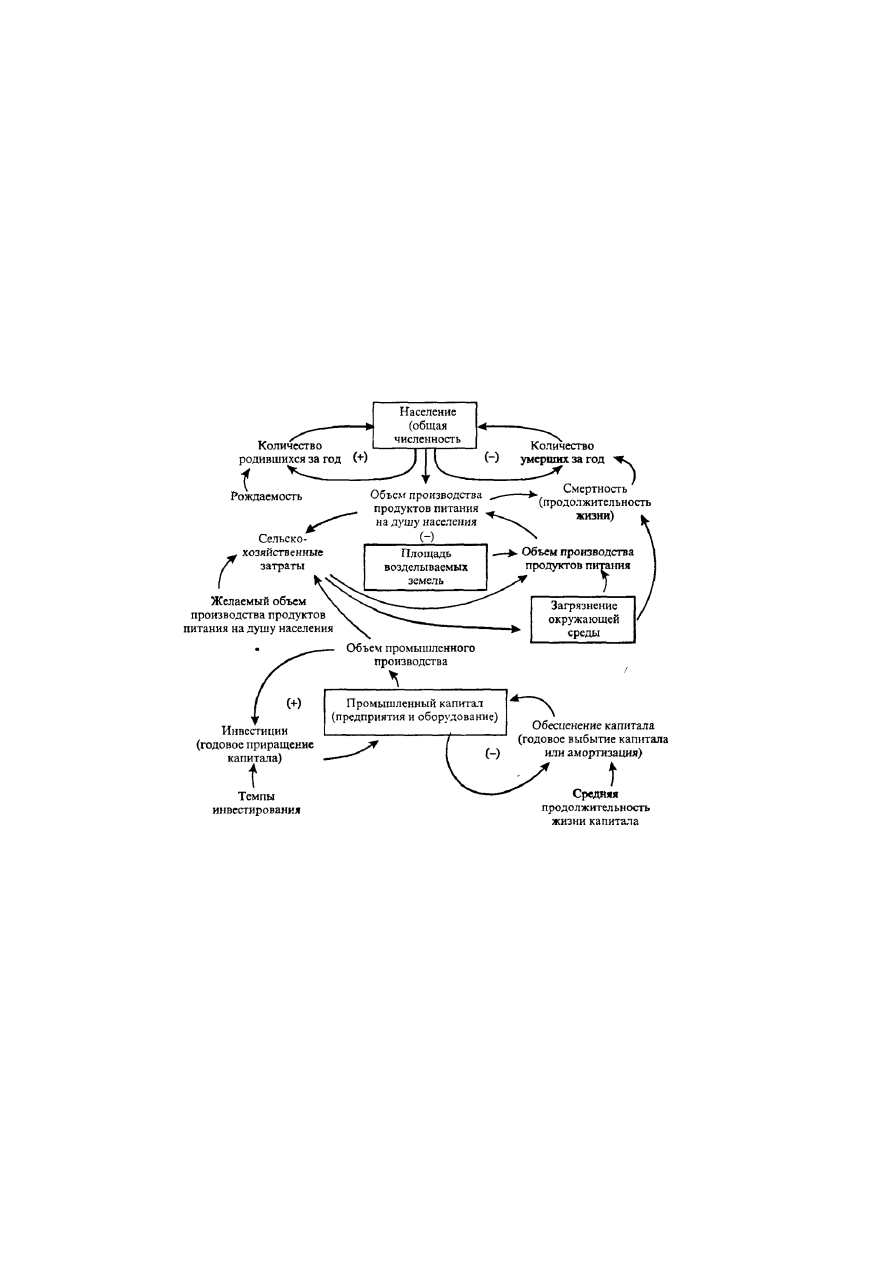
мых земель и загрязнением окружающей среды. Каждая стрелка на рисунке указывает наличие
причинной связи, которая может быть непосредственной или запаздывающей, положительной или
отрицательной.
Понятия положительной и отрицательной обратной связи взяты из теории автоматического
регулирования (раздела кибернетики). Причинно-следственная связь между двумя элементами на-
зывается отрицательной, если изменение одного элемента передается второму, возвращается от
него к первому и изменяет его в направлении, противоположном первоначальному (подавляет), и
положительной, если это изменение, возвращаясь к первому, усиливает его. Если элементов не
два, а больше, то говорят о контуре обратной связи, через которую сигнал проходит по кругу, воз-
вращаясь к источнику и влияя на него.
Некоторый набор таких рисунков графически исчерпывает модель WORLD. Однако, за ка-
ждой стрелкой - первичные взаимосвязи, за каждой из них - уравнения, в которые входит ряд па-
раметров. Фактически именно значения этих параметров и определяют результаты решения, по-
этому к их анализу привлекаются как многочисленные узкие специалисты, так и многие эмпири-
ческие (статистические) данные, собранные в десятках справочников, отчетов ООН и отдельных
государств. Количество взаимосвязанных переменных в модели WORLD-3 равно 225, параметров
- еще больше.
Рис. 7.51.
Контуры обратных связей численности населения, капитала, сельскохозяйственного
производства и загрязнения окружающей среды
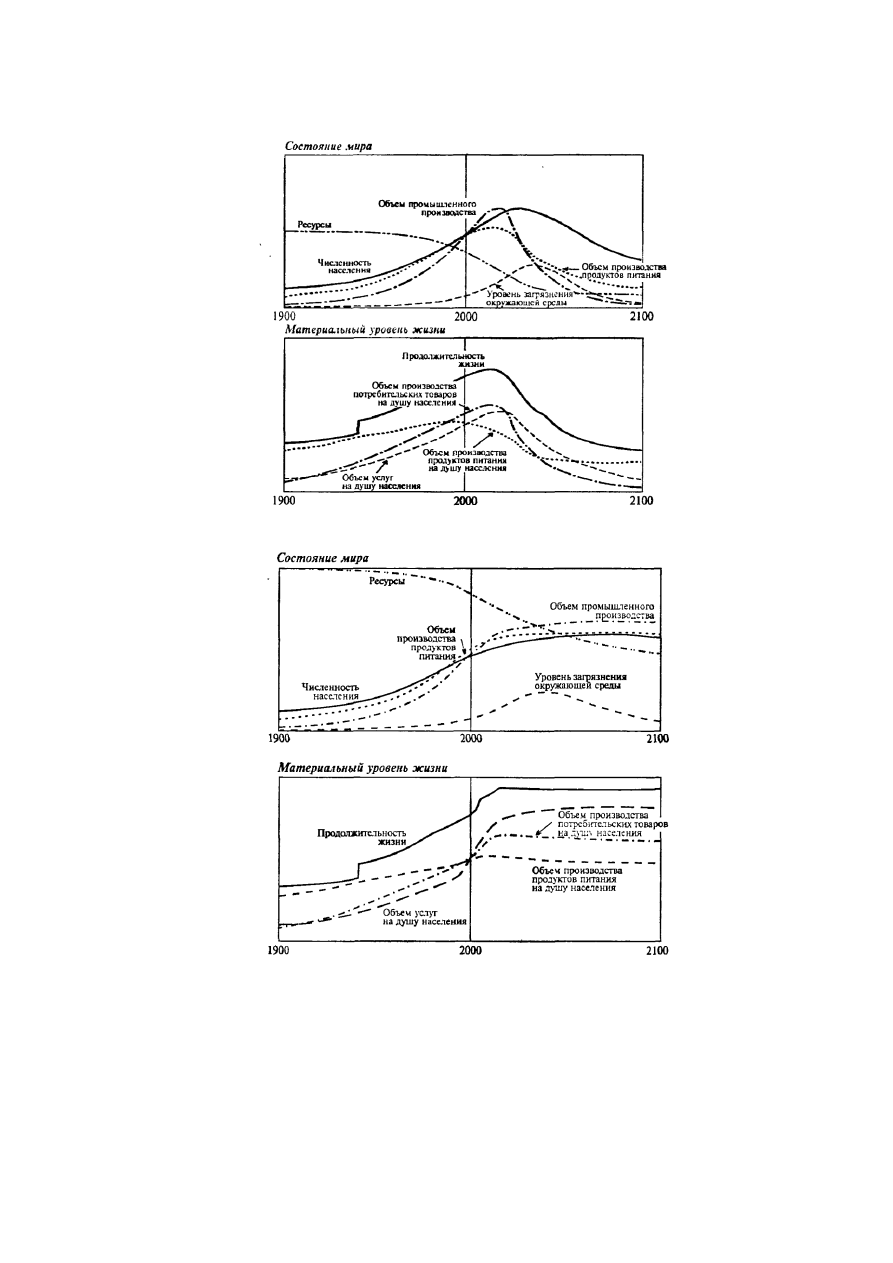
Результаты глобального моделирования.
Опубликованные «сценарии» развития челове-
чества, следующие из моделей WORLD, охватывают промежуток времени от 1900 до 2100 гг.
Первые 90 лет, уже прошедшие, позволяют «настраивать» модель, понять степень ее достоверно-
сти.
Первый из сценариев основан на гипотезе, что все будет развиваться без серьезных измене-
ний, глобальных политических катаклизмов, без особых усилий по сохранению ресурсов и
уменьшению загрязнения окружающей среды. Весьма печальные результаты такого развития ил-
люстрирует рис. 7.52 (заимствовано из того же источника).
Разумеется, временные шкалы здесь весьма расплывчаты. Что будет, если на Земле обна-
ружатся и окажутся доступными (например, в океанах) дополнительные залежи нефти и газа, дру-
гих ресурсов? Моделирование безжалостно утверждает, что это не изменит качественно характер
эволюции, а лишь сдвинет вправо точки экстремумов кривых.
Вместе с тем модель WORLD позволяет нащупать пути регулируемого развития, которое
ведет к плавному («сигмоидному») поведению основных переменных. Этот путь связан с самоог-
657
раничениями и переходом на усовершенствованные промышленные и сельскохозяйственные тех-
нологии. Иллюстрацией тому является рис. 7.53.
Итак, математическое компьютерное моделирование вторгается даже в такую сверхзадачу,
как самосохранение человека как вида.
Рис. 7.52.
Возможный вариант развития человечества на период 1900-2100 гг.
Рис. 7.53.
Более оптимистичный вариант развития человечества на тот же период времени
§ 6. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
6.1. ТЕХНИКА СТОХАСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Понятие «случайный» - одно из самых фундаментальных как в математике, так и в повсе-
дневной жизни. Моделирование случайных процессов - мощнейшее направление в современном
математическом моделировании.
Событие называется случайным, если оно достоверно непредсказуемо. Случайность окру-
658
жает наш мир и чаще всего играет отрицательную роль в нашей жизни. Однако есть обстоятельст-
ва, в которых случайность может оказаться полезной.
В сложных вычислениях, когда искомый результат зависит от результатов многих факто-
ров, моделей и измерений, можно сократить объем вычислений за счет случайных значений зна-
чащих цифр. Из теории эволюции следует, что случайность проявляет себя как конструктивный,
позитивный фактор. В частности, естественный отбор реализует как бы метод проб и ошибок, от-
бирая в процессе развития особи с наиболее целесообразными свойствами организма. Далее слу-
чайность проявляется в множественности ее результатов, обеспечивая гибкость реакции популя-
ции на изменения внешней среды.
В силу сказанного имеет смысл положить случайность в основу методов получения реше-
ния посредством проб и ошибок, путем случайного поиска.
Отметим, что выше, приведя пример имитационного моделирования - игру «Жизнь», мы
уже имели по сути дела стохастическую модель. В данном параграфе обсудим методологию тако-
го моделирования более детально.
Итак, пусть в функционале модели значения некоторых входных параметров определены
лишь в вероятностном смысле. В этом случае значительно меняется сам стиль работы с моделью.
При серьезном рассмотрении в обиходе появляются слова «распределение вероятностей»,
«достоверность», «статистическая выборка», «случайный процесс» и т.д.
При компьютерном математическом моделировании случайных процессов нельзя обойтись
без наборов, так называемых, случайных чисел, удовлетворяющих заданному закону распределе-
ния. На самом деле эти числа генерирует компьютер по определенному алгоритму, т.е. они не яв-
ляются вполне случайными хотя бы потому, что при повторном запуске программы с теми же па-
раметрами последовательность повторится; такие числа называют «псевдослучайными».
Рассмотрим вначале генерацию чисел равновероятно распределенных на некотором отрез-
ке. Большинство программ - генераторов случайных чисел - выдают последовательность, в кото-
рой предыдущее число используется для нахождения последующего. Первое из них - начальное
значение. Все генераторы случайных чисел дают последовательности, повторяющиеся после неко-
торого количества членов, называемого периодом, что связано с конечной длиной машинного сло-
ва. Самый простой и наиболее распространенный метод - метод вычетов, или линейный конгру-
энтный метод, в котором очередное случайное число
x
n
определяется
«отображением»
где
a
,
с
,
m
- натуральные числа, mod - так называемая, функция деления по модулю (остаток от де-
ления одного числа на другое по модулю). Наибольший возможный период датчика (7.69) равен
т;
однако, он зависит от
а
и
с.
Ясно, что чем больше период, тем лучше; однако реально наиболь-
шее
m
ограничено разрядной сеткой ЭВМ. В любом случае используемая в конкретной задаче вы-
борка случайных чисел должна быть короче периода, иначе задача будет решена неверно. Заме-
тим, что обычно генераторы выдают отношение
m
x
n
,
которое всегда меньше 1, т.е. генерируют по-
следовательность псевдослучайных чисел на отрезке [0,1].
Вопрос о случайности конечной последовательности чисел гораздо сложнее, чем выглядит
на первый взгляд Существует несколько статистических критериев случайности, но все они не
дают исчерпывающего ответа. Так, последовательно генерируемые псевдослучайные числа
МОГУТ
появляться не идеально равномерно, а проявлять тенденцию к образованию групп (т е. коррелиро-
вать) Один из тестов на равномерность состоит в делении отрезка [0, 1] на
М
равных частей -
«корзин», и помещения каждого нового случайного числа в соответствующую «корзину». В итоге
получается гистограмма, в которой высота каждого столбика пропорциональна количеству по-
павших в «корзину» случайных чисел (рис. 7.54).
659
Рис. 7.54.
Вид гистограммы для равномерно распределенных на отрезке [0,1] чисел при достаточ-
но большой выборке
Понятно, что при большом числе испытаний высоты столбиков должны быть почти одина-
ковыми. Однако, этот критерий является необходимым, но не достаточным; например, он «не за-
мечает» даже очень короткой периодичности Для не слишком требовательного пользователя
обычно достаточны возможности датчика (генератора) случайных чисел, встроенного в большин-
ство языков программирования. Так, в PASCAL есть функция random, значения которой - случай-
ные числа из диапазона [0, 1). Ее использованию обычно предшествует использование процедуры
randomize, служащей для начальной «настройки» датчика, т.е. получения при каждом из обраще-
ний к датчику разных последовательностей случайных чисел. Для задач, решение которых требует
очень длинных некоррелированных последовательностей, вопрос осложняется и требует нестан-
дартных решений Равномерно распределенные случайные числа - простейший случай Располагая
датчиком случайных
чисел, генерирующим числа
r
[0, 1], легко получить числа из произвольно-
го интервала [
а, b
]
.
X = a + (b - a)∙r.
Более сложные распределения часто строятся с помощью распределения равномерного.
Упомянем здесь лишь один достаточно универсальный метод Неймана (часто называемый также
методом отбора-отказа), в основе которого лежит простое геометрическое соображение. Допус-
тим, что необходимо генерировать случайные числа с некоторой нормированной функцией рас-
пределения
f(x)
на интервале [
а, b
]
.
Введем положительно определенную функцию сравнения
w(x)
такую, что
w(x)
= const и
w(x) > f(x)
на [
а, b
] (обычно
w(x)
равно максимальному значению
f(x)
на
[
а, b
]
).
Поскольку площадь под кривой
f(x)
равна для интервала [
х, х
+
dx
]
вероятности попадания
х
в этот интервал, можно следовать процедуре проб и ошибок. Генерируем два случайных числа,
определяющих равновероятные координаты в прямоугольнике
A BCD
с помощью датчика равно-
мерно распределенных случайных чисел:
x = a + (b - a)∙r, y = w∙r
и если точка
М(х, у)
не попадает под кривую
f(x)
, мы ее отбрасываем, а если попадает - оставляем
(рис. 7.55). При этом множество координат
х
оставленных точек оказывается распределенным в
соответствии с плотностью вероятности
f(x)
.
660
Рис. 7.55.
Метод отбора-отказа. Функция
w(x)
=
f
max
Этот метод для ряда распределений не самый эффективный, но он универсален, прост и по-
нятен. Эффективен он тогда, когда функция сравнения
w(x)
близка к
f(х)
. Заметим, что никто не
заставляет нас брать
w(x)=
const на всем промежутке [
а, b
]
.
Если
f(x)
имеет быстро спадающие
«крылья», то разумнее взять
w(x)
в виде ступенчатой
функции.
6.2
.
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ В СИСТЕМАХ МАССОВОГО ОБ-
СЛУЖИВАНИЯ
Кому
не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать
покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его
распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько
раз на короткие гудки, нервничать и оценивать - дозвонюсь или нет? Из таких «простых» проблем
в начале XX века родилась весьма непростая наука - теория массового обслуживания, использую-
щая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и
численных методов. Основоположником ее стал датский ученый А.К.Эрланг, исследовавший про-
блемы функционирования телефонных станций.
Впоследствии выяснилось, что новая наука имеет многочисленные выходы в экономику,
военное дело. организацию производства, биологию
и экологию; по ней
написаны десятки книг,
тысячи журнальных статей.
Компьютерное моделирование при решении задач массового обслуживания. реализуемое в
виде метода статистических испытаний (метода Монте-Карло), хоть и не является в теории массо-
вого обслуживания основным, но играет в ней важную роль. Основная линия в ней - получение
результатов аналитических, т.е. представленных формулами. Однако, возможности аналитических
методов весьма ограничены, в то время как метод статистических испытаний универсален и весь-
ма прост для понимания (по крайней мере кажется таковым).
Типичная задача: очередь к одному «продавцу». Рассмотрим одну из простейших задач
данного класса. Имеется магазин с одним продавцом, в который случайным образом входят поку-
патели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей
несколько, выстраивается очередь.
Вот аналогичные задачи:
• ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки;
•травмопункт и больные, пришедшие на прием по случаю травмы (т.е. без системы предва-
рительной записи);
• телефонная станция с одним входом (или одной телефонисткой) и абоненты, которых при
занятом входе ставят в очередь (такая система иногда практикуется);
• сервер локальной сети и персональные машины на рабочем месте, которые шлют сообще-
ние серверу, способному воспринять разом и обработать не более одного сообщения.
Будем для определенности говорить о магазине, покупателях и продавце. Рассмотрим воз-
никающие здесь проблемы, которые заслуживают математического исследования и, как выясняет-
ся, весьма серьезного.