ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример выполнения задания №6
Расчет статически неопределимой фермы.
F1 = 3 кН
F 2 = 5 кН
F 3 = 4 кН
F 4 = 5 кН
F 5 = 3 кН
l = 18 м
h1 = 3 м
h2 = 5 м
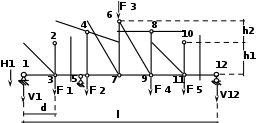
Рисунок 7.1 – Заданная ферма.
Решение.
1. Определяем степень статической неопределимости:
Так как система внешне статически неопределима, то степень статической неопределимости определяем по формуле:
nСТ = СОП – 3 = 4 – 3 = 1,
таким образом, ферма (рис 7.1) один раз статически неопределима.
2. Выбираем основную систему: так как ферма симметричная, то лучше отбрасывать одну центральную опорную связь.
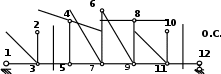
Строим эквивалентную систему:
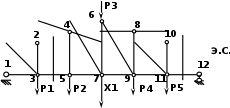
3. Каноническое уравнение метода сил выглядит следующим образом:
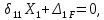
4. Определяем внутренние усилия во всех стержнях фермы.
-
Определяем аналитически усилия в каждом стержне в основной системе от действия силы Х1 = 1 (в единичном состоянии). Все расчеты заносим в таблицу (столбец 4).
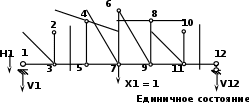
Определяем опорные реакции
Σ Х = 0, H1 = 0
Σ М1 = 0, Х1·3d - V12·l= 0, Х1·9 - V12·18 = 0, V12 = 0,5(т)
Σ М12 = 0, - Х1·3d + V1·l= 0, -Х1·9 + V19·18 = 0, V1 = 0,5(т)
Σ Y = 0, V1 + V12 - Х1 = 0, 0 = 0
Реакции найдены верно.
Определяем внутренние усилия во всех стержнях фермы в единичном состоянии. Результаты вычислений заносим в таблицу.
cos α = l13 / l12 = 0,707 sin α = l23 / l12 = 0,707
cos β = l4К / l24 = 0,316 sin β = l2К / l24 = 0,949
sin γ = l67 / l56 = 0,587
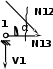 | (способ вырезания узлов) Σ Y = 0, V1 + N12· sin α = 0, N12 = - V1 / sin α N12 = - 0,5 / 0,707 = - 0,707 (кН) (способ вырезания узлов) Σ Х = 0, N13 + N12· cos α = 0, N13 = - N12· cos α N13 = 0,707· 0,707 = 0,5 (кН) |
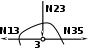 | (по признакам) N35 = N13 , N35 = 0,5(кН), N23 = 0 |
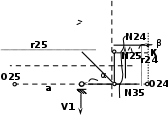 | (способ моментной точки) Σ М О24 = 0, V1· 6 + N24· r24 = 0, N24 = - V1· 6/ r24 , r24 = sin β· l45 = 3,795(м) N24 = - 0,5· 6/ 3,795 =- 0,791(кН) (способ моментной точки) Σ М О25 = 0, -V1· а + N25· r25 = 0, N25 = V1· а / r25 , а = 6(м), r25 = cos α· (а + 6)= 8,485(м) N25 = 0,5· 6 / 8,485 = 0,354(кН) |
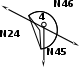 | (по признакам) N46 = N24 , N46 = - 0,791 (кН), N45 = 0 |
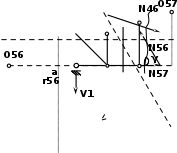 | (способ моментной точки) Σ М О57 = 0, V1· 9 - N24· 5 = 0, N57 = V1· 9 / 5 , N57= 0,5· 9 / 5 = 0,9 (т) (способ моментной точки) Σ М О56 = 0, -V1·а - N56· r56 = 0, r56 = sin γ· (а+6) = 10,29(м) N56 = - V1·а / r56 N56 =- 0,5·6 /10,29 = - 0,292(т) |
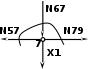 | (по признакам) N79 = N57 , N79 = 0,9 (т), N67 = Х1 , N67 = 1 (т) |
Так как ферма симметричная и нагрузка также симметричная, то усилия в симметричных стержнях будут равны. Следовательно, рассчитываем только половину фермы, а остальные усилия запишем по аналогии.
-
Определяем аналитически усилия в каждом стержне в основной системе от действия заданной внешней нагрузки ( в грузовом состоянии). Все расчеты заносим в таблицу (столбец 5).
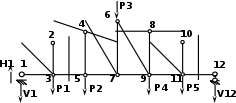
Определяем опорные реакции:
Σ Х = 0, H1 = 0
Σ М1 = 0, F1·3+ F2·6+ F3·9+ F4·12+ F5·15 - V12·18 = 0, V12 =10(т)
Σ М12 = 0, V1·18 - F5·3 - F4·6 - F3·9 - F2·12 - F1·15 = 0, V1 =10(т)
Σ Y = 0, V1 + V12 - F5 - F4 - F3 - F2 - F1 = 0, 0 = 0
Реакции найдены верно.
Определяем внутренние усилия во всех стержнях фермы в грузовом состоянии. Результаты вычислений заносим в таблицу.
cos α = l13 / l12 = 0,707 sin α = l23 / l12 = 0,707
cos β = l4К / l24 = 0,316 sin β = l2К / l24 = 0,949
sin γ = l67 / l56 = 0,587
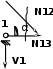 | (способ вырезания узлов) Σ Y = 0, V1 + N12· sin α = 0, N12 = - V1 / sin α N12 = - 10 / 0,707 = -14,14 (т) (способ вырезания узлов) Σ Х = 0, N13 + N12· cos α = 0, N13 = - N12· cos α N13 = 14,142· 0,707 = 10 (т) |
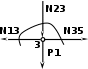 | (по признакам) N35 = N13 , N35 = 10 (т), N23 = Р1 , N23 = 3 (т) |
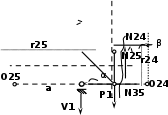 | (способ моментной точки) Σ М О24 = 0, V1· 6 + N24· r24 - Р1· 3 = 0, N24 = (Р1· 3 - V1· 6)/ r24 , r24 = sin β· l45 = 3,795(м) N24 = (3· 3 - 10· 6)/ 3,795 =-13,44(т) (способ моментной точки) Σ М О25 = 0, -V1· а + N25· r25 + Р1·(а+3)= 0, N25 = (V1· а -Р1·(а+3))/ r25 , а = 6(м), r25 = cos α· (а + 6)= 8,485(м) N25 = (10· 6 - 3· 9)/ 8,485 = 3,889(т) |
 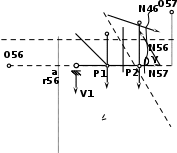 | (по признакам) N46 = N24 , N46 = -13,44 (т), N45 = 0 |
| | (способ моментной точки) Σ М О57 = 0, V1· 9 - Р1· 6 - Р2· 3 - N24· 5 = 0, N57 = (V1· 9 - Р1· 6 - Р2· 3)/ 5 , N57= (10· 9 - 3· 6 - 5· 3)/ 5 = 11,4(т) (способ моментной точки) Σ М О56 = 0, Р1·(3+а) - V1·а - Р2·(6+а) – N56· r56 = 0, r56 = sin γ· (а+6) = 10,29(м) N56 =(Р1·(3+а) - V1·а + Р2·(6+а))/ r56 N56 =(3·9- 10·6 +5·12)/10,29 =2,624(т) |
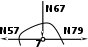 | (по признакам) N79 = N57 , N79 = 11,4 (т), N67 = 0 |
Так как ферма симметричная и нагрузка также симметричная, то усилия в симметричных стержнях будут равны. Следовательно, рассчитываем только половину фермы, а остальные усилия запишем по аналогии.
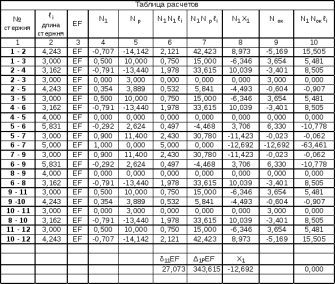
5. Исходя из найденных усилий, рассчитываем таблицу.
Находим коэффициенты канонического уравнения:
δ11 =
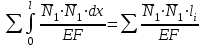
(суммируем столбец 4)
Δ1р =
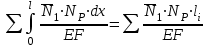
(суммируем столбец 5)
6. Из канонического уравнения находим
Χ1 = -Δ1Р/ δ11 = -343,603/27,073 = -12,692 т
7. Окончательные усилия в каждом стержне определим по формуле
Результаты также занесем в таблицу(столбец 8,9):
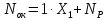
8. Для найденных значений внутренних усилий в стержнях фермы
выполним проверки:
-
Статическая проверка – любой вырезанный узел должен находиться в состоянии статического равновесия. Для этого вырежем узел в котором сходится наибольшее количество стержней – узел 5
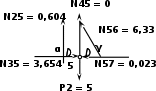
Σ Х = 0, -N35 - N57 – N25· cos α + N56· cos γ = 0,
- 3,654 - 0,023 + 0,604· 0,707 + 6,33· 0,515 = 0,009 ≈ 0
Σ Y= 0, - Р2 – N25· sin α + N56· sin γ = 0,
- 5 - 0,604· 0,707 + 6,33· 0,587 = 0,0017≈ 0
-
Деформационная проверка
Δ1ок =
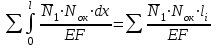 = 0
= 0 Деформационную проверку выполним непосредственно в таблице (столбец 10)
Вывод: Проверки выполнены, значит, ферма рассчитана верно.