Файл: Решение 1 Это знакочередующий ряд. Исследуем его по теореме Лейбница.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание по дисциплине
«Математика»
На основе полученной в ходе курса информации, выполните представленные нижеперечисленные задания по дисциплине «Математика».
Дисциплина «Математика»
Задание 1.
Выясните, сходятся данные ряды абсолютно, условно или же расходятся.
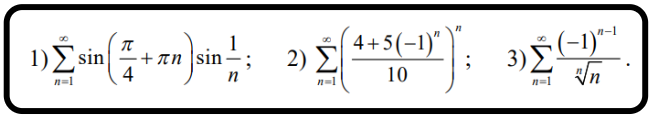
Решение:
1)
Это знакочередующий ряд. Исследуем его по теореме Лейбница
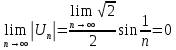
Т.к.
и 
- то по теореме Лейбница ряд сходитсяИсследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда, чтобы узнать, сходится исходный ряд абсолютно или условно.
- общий член гармонического ряда. Гармонический ряд расходится
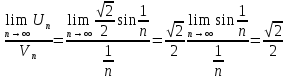
По предельному признаку сравнения ряд
расходится. Значит исходный ряд сходится условно.
Ответ: ряд сходится условно.
2)
Это знакочередующий ряд. Исследуем на сходимость ряд, составляенный из абсолютных величин членов данного ряда. Если он сходится – то и данный ряд сходится, причем абсолютно.
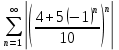
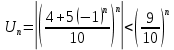
Ряд
- это ряд геометрической прогрессии
, он сходится при 
. В данном случае: 
– ряд сходитсяПо признаку сравнения ряд
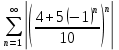сходитсяЗначит исходный ряд сходится абсолютно
Ответ: ряд сходится абсолютно
Это знакочередующий ряд.
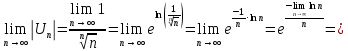
Необходимый признак сходимости ряда не выполняется. Ряд расходится.
Ответ: ряд расходится.
Задание 2.
Выпущено 900 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.
Решение: 900-(5+10+20+50)=815(билеты без выигрыша)
P(x=0)=815/900=0.906 ; P(x=10)= 50/900=0.056; P(X=50) = 20/1000=0.022;
P(X=100) = 10/1000=0.011; P(X=500) = 5/1000=0.006
| Значение xi | 0 | 10 | 50 | 100 | 500 |
| Вероятности pi | 0.906 | 0.056 | 0.022 | 0.011 | 0.006 |