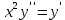
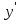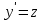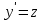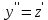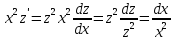
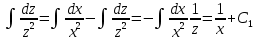
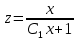
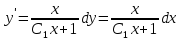
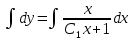
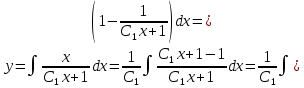
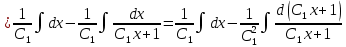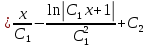
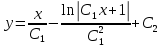
Задача №2. Решить уравнение, допускающее понижения порядкаРешение:В данном уравнении второго порядка в явном виде не участвует переменная y. Заменим первую производную новой функцией z, которая зависит от x: .Если ,то . Цель проведённой замены – понизить степень уравнения.Проинтегрируем обе части равенстваВозвращаемся к переменной у.Интегрируем обе части равенства: = Ответ: Общее решение Задача №3. 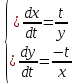Решить систему уравнений.Решение:Из уравнения 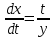выражаем переменную

---

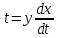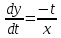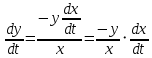
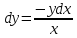
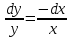
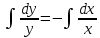
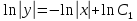
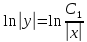
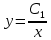
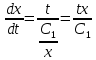
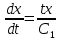
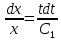
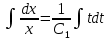
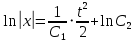
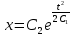
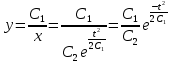
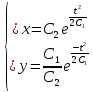
. Подставляем это выражение в уравнение : Разделяем переменные: Интегрируем обе части: Подставляем полученное выражение в уравнение Разделяем переменные и интегрируем обе части   Тогда Ответ: Общее решение системы уравнений Задача №4. Вероятность появления события в каждом испытании равна 0,7. 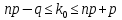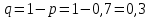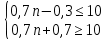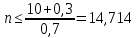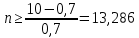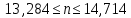Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?Решение: Наивероятнейшее число определяется двойным неравенством:В нашем случае Из первого неравенства: Из второго неравенства:Так как n – целое число, получаем n = 14.Ответ: 14 испытаний.

---

Смотрите также файлы

• азастан республикасы білім жне ылым министрлігі МАыстау гуманитарлы техникалы университеті.docx

• Цифровая трансформация в менеджменте синергия вопросы от теста, для просмотра ответов, перейдите по ссылке ниже вопроса это множество составляющих единство элементов,.docx

• Теория систем и систеМный анализ.docx

• белгородский государственный национальный исследовательский университет (ниу БелГУ) медицинский институт.pdf

• Номенклатура дел.doc