Анионные и катионные ПАВ при длине алкильного радикала от С₈ до С₁₄ обладают ярко выраженной антифаговой активностью.

Антимикробное действие ПАВ связывают с их влиянием на проницаемость клеточных мембран, а также ингибирующим действием на ферментативные системы микроорганизмов.

   Неионогенные ПАВ практически не обладают противомикробным действием.

орбционные процессы.

 

      Адсорбция растворенных веществ на поверхности твердого тела является довольно сложным процессом, поскольку участниками его будут уже не два компонента, а по меньшей мере три.

       Адсорбцию как самопроизвольный процесс накопления одного вещества на поверхности другого следует отличать от абсорбции, Поглощение молекул газа или парообразного вещества может не ограничиться лишь их накоплением в поверхностном слое - они диффундируют в толщу (объем) адсорбента. Именно такой процесс и называетсяабсорбцией. Растворение газа в жидкости с образованием гомогенного раствора может рассматриваться в качестве примера абсорбции. Абсорбция может наблюдаться и при поглощении газов твердыми телами. Так, 1 см³ губчатой платины поглощает 800 см³ водорода. Эта способность губчатой платины, как известно, используется в технологиях изготовления водородного электрода.

     На практике трудно провести четкую границу между адсорбцией и абсорбцией, и потому оба процесса объединяют одним понятием --сорбция.

 

 Адсорбцияна границе раздела жидкость -газ и жидкость - жидкость.

Любая система в соответствии со вторым началом термодинамики стремится самопроизвольно перейти в такое состояние, в котором она обладает минимальным запа­сом энергии Гиббса (G_s=  σ•S). Следовательно, она стремится к минимуму поверхностной энергии Гиббса(G_s→G_min).

Поверхностное натяжение при прочих равных условиях определяется природой вещества. Поэтому система, образованная одним компонентом (σ = const), может понизить запас своей поверхностной энергии Гиббса в данных условиях только одним путем -- принять форму, при которой поверхность раздела фаз минимальна

---

 (S→S_min).Из разных геометрических форм одинаковой массы данного вещества минимальной поверхностью обладает сфера. Этим, в частности, объясняется сфери­ческая форма падающих капелек жидкости (дождя).

Система, состоящая больше чем из одного компонента, помимо уменьшения поверхности, может понизить поверхностную энергию Гиббса перераспределением растворенного вещества между объемом фазы и поверхностным (пограничным) слоем.

Теоретически можно представить три случая распределения растворенного вещества между граничным слоем и объемом фазы        (рис. 4 а, б, в).

1.концентрация растворенного вещества в поверхностном слое больше, чем в объеме фазы(С_v);

2.концентрация растворенного вещества в поверхностном слое меньше, чем в объеме фазы;

3.концентрация растворенного вещества в поверхностном слое такая же, как и в объеме фазы.

ПАВ накапливаются в поверхностном слое (C_Ω > C_V). При этом система уменьшает запас поверхностной энергии Гиббса, ПИВ накапливаются в объеме фазы (C_Ω< C_V), так как в этом случае запас поверхностной энергии Гиббса уменьшается.

У веществ, не влияющих на поверхностное натяжение растворителя, концентрации в поверхностном слое и в объеме фазы будут одинаковы   (C_Ω=C_V), так как перераспределение вещества не меняет поверхностное натяжение.

Самопроизвольное изменение концентрации растворенного вещества на границе раздела фаз называется адсорбцией.



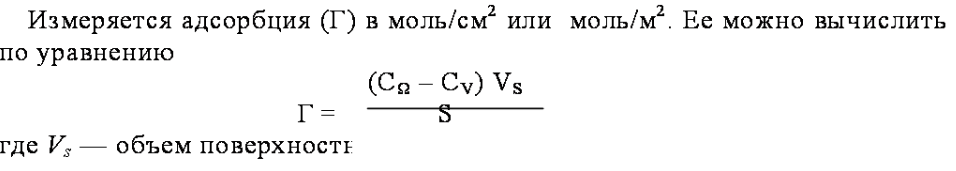
Адсорбция ПАВ положительна (Г > 0), поскольку C_Ω > C_V. Адсорбция ПИВ отрицательна (Г  0),так какC_Ω

---

< C_V

---

.Для веществ, не влияющих на величину поверхностного натяжения, Г = 0, здесь C_Ω= C_V.

Адсорбция вещества X представляет собой обратимый процесс, заканчивающийся установлением адсорбционного равновесия. При равновесии скорость адсорбции равна скорости обратного процесса -- десорбции:



    Зависимость адсорбции от равновесной концентрации растворенного вещества при постоянной температуре называют изотермой адсорбции.

Уравнение  Гиббса  и  его  анализ.

Адсорбцию на границе раздела жидкость -- газ непосредственно не измеряют, а вычисляют с помощью уравнения Гиббса, которое выведено на основании 2-го начала термодинамики


Проверка уравнения Гиббса проводилась различными методами и показала хорошее совпадение экспериментально определенной величины адсорбции и вычисленной по уравнению Гиббса (табл.2).где Г -- количество адсорбированного вещества, моль/м²; с -- молярная концентрация растворенного вещества, моль/дм ;

R-- газовая постоянная, равная 8,32 Дж/(моль«К); --

поверхностная активность.

Таким образом, для нахождения адсорбции необходимо знать поверхностную активность при данной концентрации и температуре.

Таблица 2.Теоретические и экспериментальные значения адсорбции

ПАВ	Гэкс• 107, моль/см2	Гвыч • 107, моль/см2
Фенол	4,1	4,8
Капроновая кислота	6,2	6,3
Гидрокоричная кислота	5,6	5,1

---

График типичной экспериментальной изотермы представлен на рис. 5. При очень малых равновесных концентрациях адсорбция пропорциональна концентрации, что находит выражение в прямолинейном ходе изотермы адсорбции (участок 1). С дальнейшим ростом концентрации рост адсорбции замедляется, и этот участок изотермы изображается параболической кривой (участок 2).

Рис. 5. Изотерма адсорбции поверхностно-активного вещества на границе раздела раствор - газ.

    При больших концентрациях адсорбция достигает предельного значения (Г_∞), которое не изменяется с дальнейшим увеличением кон­центрации растворенного вещества (участок 3). Графически этот участок изображается горизонтальной прямой.

Помимо концентрации растворенного вещества, адсорбция зависит от природы вещества и температуры. Для веществ одного и того же гомологического ряда адсорбция изменяется в соответствии с правилом Дюкло -- Траубе (рис. 6). С ростом температуры адсорбция уменьшается.

 

Изотермы Фрейндлиха и Лэнгмюра.

Для описания экспериментально наблюдаемой изотермы предложено более 20 уравнений. Из них наиболее часто в медико-биологических исследованиях используют изотермы Фрейндлиха и Лэнгмюра.

1.Изотерма Фрейндлиха:

Г = К_фСⁿ

где К_ф-- константа, численно равная адсорбции при равновесной концентрации, равной единице; n -- константа, определяющая кривизну изотермы адсорбции, ее значение колеблется в пределах от 0,1 до 0,6.

Изотерма Фрейндлиха представляет собой уравнение параболической кривой. Оно применимо лишь при средних значениях равновесных концентраций. Для нахождения постоянных в уравнении Фрейндлиха его логарифмированием приводят к уравне­нию прямой:

lgГ = lgK_ф + п 1gc.

Отрезок ординаты от начала осей координат до ее пересечения с прямой численно равен lgK_ф, а тангенс угла φ наклона прямой численно равен 

---

Смотрите также файлы

• Занятие 2 тема 2 финансы и финансовая система рф задание 1.docx

• Презентация по обещтвознанию студентки группы 13а василенко оксаны.pptx

• Тема Матрица.docx

• рпп.docx

• Занятие 2 тема 2 финансы и финансовая система рф задание 1.docx