Математические модели, передаточные функции

элементов систем автоматического управления
Решение большинства задач теории автоматического управления (ТАУ) связано с использованием математических моделей (ММ) элементов и систем автоматического управления.

Под ММ понимается математическое описание зависимости между входными и выходными величинами (сигналами) исследуемого элемента или системы. Различают ММ установившегося состояния (статики) и ММ динамики, описывающие изменение выходных величин при изменении входных. ММ динамики более полные, из них можно получить уравнения (ММ) статики. Наоборот, из уравнений статики получить уравнения динамики нельзя.

Существуют различные формы уравнений динамики.

Наиболее общей, широко распространённый в инженерной практике первичной формой ММ, являются дифференциальные уравнения (ДУ), которые составляются на основе физических законов определяющих протекающие процессы.

Обычно с целью упрощения задачи получения ММ систем, системы разбивают на элементарные составные части (звенья) направленного действия, получают модели этих звеньев, на основании которых затем составляют ММ сколь угодно сложных систем.

Звеном направленного действия называется участок системы (звено) на который не оказывает воздействие последующий участок системы и который сам не влияет на состояние предыдущего. Сигнал в звене передается только в одном направлении. В этом случае каждое звено может быть представлено отдельной ММ, что упрощает получение ММ отдельных звеньев системы и ММ системы в целом.


В общем случае дифференциальное уравнение звена или системы в канонической форме имеет вид:

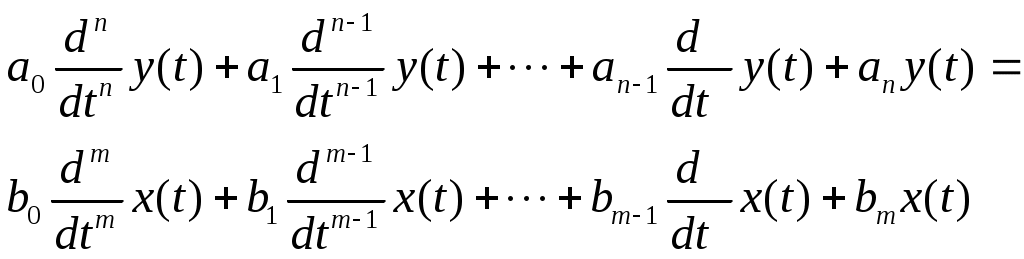(1)



Где

---

x(t), y(t) – соответственно входная и выходная величины. Обратите внимание: при записи дифференциального уравнения выходная величина располагается в левой части уравнения, а входная величины в правой.

a_i,b_i - коэффициенты, определяемые физическими параметрами (константами) характеризующими скорость протекания процессов в описываемых элементах и системах. Такими константами являются, например, массы движущихся тел, индуктивности, ёмкости, сопротивления электрических цепей, теплоёмкости нагреваемых элементов.

Если коэффициенты уравнения не изменяются во времени, звенья называются стационарными, если изменяются – нестационарными.

Для линейных систем состоящих только из стационарных звеньев справедлив принцип суперпозиции (наложения). Суть принципа – реакция системы на несколько одновременно действующих воздействий равна сумме реакций на каждое воздействие в отдельности. Принцип суперпозиции существенно облегчает решение ряда задач.

Удобной формой записи линейных дифференциальных уравнений является символическая или операторная форма. При этом используются следующие обозначения:

- символ дифференцирования;



Дифференциальное уравнение (1) в операторной форме представляется в виде:

(2)

Или в компактной форме: , (3)

где: А(p) – собственный (характеристический) оператор (полином) характеризует собственное (свободное) движение элемента, то есть движение при отсутствии внешних воздействий;

B(p) – оператор воздействия (входной), определяет характер внешних воздействий. Старшая степень полинома при входной величине должна быть меньше или равна старшей степени полинома при выходной величине (m ≤ n). Если это условие не выполняется

---

, то имеет место ММ физически не реализуемого элемента.

Уравнение (2) при n < 3 принято записывать в стандартной форме. При этом коэффициенты при входной и выходной величинах должны быть равны 1.

Пример: задано дифференциальное уравнение с характеристическим полиномом второй степени:



Приведем уравнение к стандартной форме.

Разделим правую и левую части уравнения на коэффициент при выходной величине a₂ и коэффициент, полученный при входной величине, вынесем за скобки:



Введем следующие обозначения коэффициентов:

; ; ; .

После подстановки обозначений получим следующий вид дифференциального уравнения в операторной форме:

,

где: К_ст. – статический коэффициент усиления (передачи) звена (коэффициент передачи звена в установившемся состоянии при постоянном сигнале на входе звена);

Т, Т₁, Т₂ - постоянные времени, имеющие размерность секунды.

Понятие передаточной функции

Решение задач теории автоматического управления с использованием математических моделей в виде дифференциальных уравнений затруднено из-за сложности получения математических моделей систем на базе моделей ее звеньев.

Более удобной формой математических моделей звеньев и систем имеющей широкое применение в инженерной практике является математическое описание в виде передаточных функций. Основным достоинством такого вида математических моделей является простота получения моделей сложных систем (передаточных функций) на основе передаточных функций звеньев этих систем и простых правил преобразования структурных схем.

---

Передаточные функции звеньев получают на основе их дифференциальных уравнений. Для этого первоначально необходимо получить изображение по Лапласу дифференциального уравнения рассматриваемого звена.

Формально изображение дифференциального уравнения по Лапласу выполняется путем замены в дифференциальном уравнении (2) символа дифференцирования p на переменную преобразования Лапласа S и соответственно .

При этом изображение дифференциального уравнения по Лапласу примет вид:

или

в компактной записи: , где:

А(S) = (a₀Sⁿ + a₁S^n-1 + … +a_n-1S + a_n);

B(S)= (b₀S^m + b₁S^m-1 + … +b_m-1S + b_m);

X(S) и Y(S) соответственно изображение по Лапласу входной и выходной величин.

Взяв отношение изображения по Лапласу выходной величины к изображению входной, получим:

- выражение передаточной функции в общем виде.

Таким образом: передаточная функция есть отношение изображения по Лапласу выходной величины звена или систем к изображению входной при нулевых начальных условиях или иначе это отношение изображения по Лапласу полинома правой части дифференциального уравнения звена или системы к изображению полинома левой части.

Введем понятие статического коэффициента передачи звена или системы, то есть коэффициента передачи звена или системы в установившемся состоянии (параметры звена и входной сигнал неизменны).

Статический коэффициент передачи звена определяется по выражению:

---

Пример 1 Задана пассивная электрическая цепь (четырехполюсник). Требуется получить: дифференциальное уравнение, передаточную функцию и Кст.


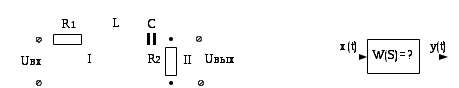
Решение: Данная электрическая цепь называется пассивной, так как не содержит источника энергии. Используя операторное представление сопротивлений электрической цепи на основании первого закона Кирхгофа (сумма падений напряжений в контуре равна нулю) составим следующие уравнения для первого и второго контуров:

(1), (2).

Из (2) выразим токI: . Подставив выражение для тока I в уравнение (1), получим:

(3).

Избавимся от дроби и выходную величину (U_вых) и полином перед ней перенесём в левую часть уравнения, а входную величину (U_вх) в правую:

(4).

Введем обозначения:

L*C = T₂², (R₁ + R₂)*C = T₁,R₂ *C = T.

После подстановки получим:

(T₂² p² + T₁p + 1)U_вых(t) = TpU_вх(t) (5)

- дифференциальное уравнение рассматриваемой электрической цепи в операторной форме.

Заменив в (5) р на s и взяв отношение изображения по Лапласу выходного сигнала U_вых(S) к изображению входного сигнала U_вх(S), получим выражение передаточной функции для рассматриваемой электрической цепи:

– данная электрическая цепь является звеном второго порядка, так как старшая степень полинома знаменателя равна двум.

Далее по полученному выражению передаточной функции определим значение статического коэффициента усиления:

---

Смотрите также файлы

• Подходящие сортаСмотреть всеКак добавить свои товарыЦены на зерно (2023 год).pdf

• План мероприятий по сохранению и укреплению здоровья и коррекции факторов риска Заключение.docx

• История появления витаминов.pptx

• Учебник по мхк. От истоков до xvii в. 10 класс Даниловой Г. И. и учебник по всеобщей истории с древнейших времен до конца xix в..doc

• Анатомия это наука, изучающая форму и строение.docx