Вывод: в установившемся состоянии при U_вх(t) – const. и не равном 0,напряжение на выходе пассивного четырехполюсника U_вых равно 0, так как после окончания переходного процесса после подачи на вход схемы U_вх(t) – const., конденсатор оказывается полностью заряжен и, в идеальном состоянии, в дальнейшем не проводит постоянный электрический ток, т.е. является разрывом электрической цепи. Отсутствие тока через сопротивление R₂ определяет значение U_вых = 0.
Пример 2 Задана схема усилителя постоянного тока с большим коэффициентом усиления охваченного отрицательной обратной связью. Требуется составить дифференциальное уравнение усилителя, найти передаточную функцию относительно напряжений U₁ и U₂, статический коэффициент передачи.


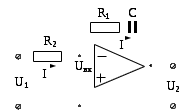
Решение: Для заданной схемы, аналогично решению предыдущей задачи, запишем уравнения Кирхгофа. При этом, в виду малости значения U_вх (так как, ) не учитываем. Тогда:

(6)

или (7)

Решая совместно (6) и (7) путем исключения переменной I получим дифференциальное уравнение усилителя:



Введем обозначения постоянных времени: и перепишем дифференциальное уравнении в операторной форме в виде:

---

, получим изображение этого уравнения по Лаплассу: и далее передаточную функцию: , и статический коэффициент передачи: .

Стремление К_ст к бесконечности определяется наличием конденсатора в цепи обратной связи усилителя (выходное напряжение усилителя возрастает до его насыщения).
Пример 3: Найти дифференциальное уравнение, передаточную функцию относительно напряжений U₁ и U₂ и статический коэффициент передачи мостовой пассивной электрической цепи приведенной на рисунке.

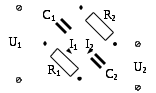
Решение: Запишем уравнения для токов плеч моста I₁ и I₂ в операторной форме:

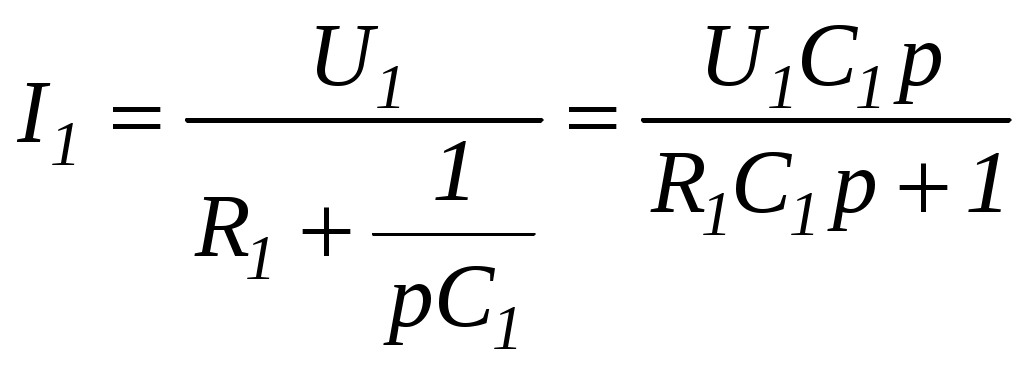; (8)

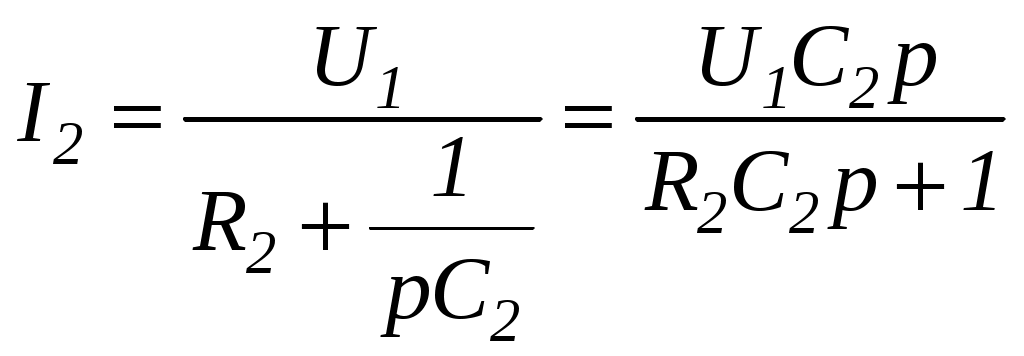. (9)

Определим выходное напряжение U₂ как разность напряжений на элементах R₁ и C₂:

.

Подставляя в это выражение значения токов из (8) и (9), находим зависимость выходного напряжения U₂ от входного U<sub>1

.</sub>

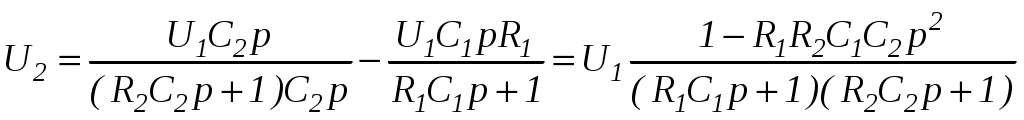Введем обозначения постоянных времени: , и представим полученное дифференциальное уравнение в операторной форме в следующем виде:

.

Представим полученное уравнение в виде изображения по Лаплассу:

.

Из этого уравнение получим выражение передаточной функции:

.

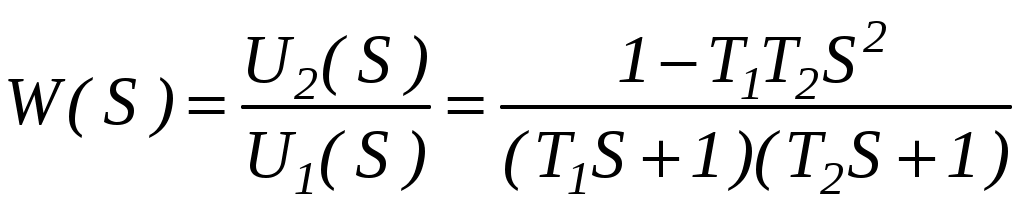Определим выражение для расчета статического коэффициента передачи:

---

.

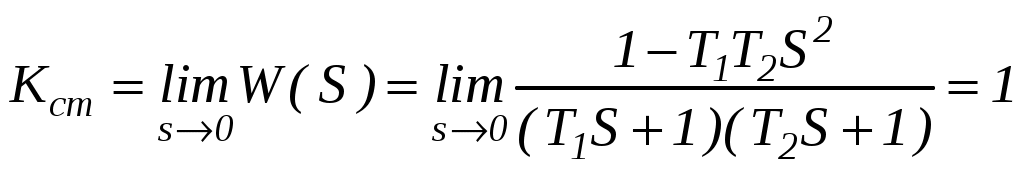Таким образом, в установившемся состоянии напряжение на выходе рассматриваемой мостовой схемы равно напряжению на её входе.
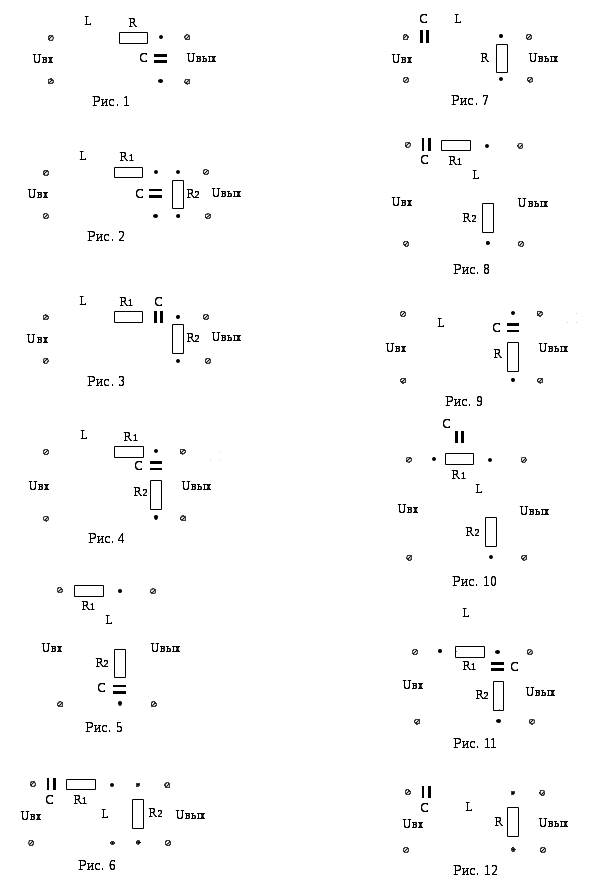
Примеры для самостоятельной работы

Определить дифференциальные уравнения, передаточные функции, статические коэффициенты усиления для звеньев с приведенными схемами:

---

Смотрите также файлы

• Подходящие сортаСмотреть всеКак добавить свои товарыЦены на зерно (2023 год).pdf

• План мероприятий по сохранению и укреплению здоровья и коррекции факторов риска Заключение.docx

• История появления витаминов.pptx

• Учебник по мхк. От истоков до xvii в. 10 класс Даниловой Г. И. и учебник по всеобщей истории с древнейших времен до конца xix в..doc

• Анатомия это наука, изучающая форму и строение.docx