ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 66
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Колебания системы с конечным числом степеней свободы, приведенная система. Кинетическая и потенциальная энергия малых свободных колебаний. Уравнение малых колебаний системы около положения устойчивого равновесия.
Детали или механизмы системы на практике являются сложной упругой системой с бесконечным числом степеней свободы. Для определения положения точек при колебаниях в любой момент времени необходимо найти функцию времени и координат точек. При расчетах упругая система заменяется более простой системой с конечным числом степеней свободы – приведенная система.
Кинематическая энергия системы с
степеней свободы:
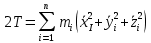
Если выполняется переход к обобщенным координатам:
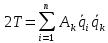
инерционные коэффициенты.
Для колебаний возле положения устойчивого равновесия разложение коэффициентов
в ряд по степеням 
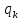ограничивается рассмотрением постоянного коэффициента 
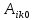, остальные же не рассматриваются ввиду их малости.
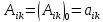
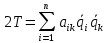
Потенциальная энергия системы может быть выражена через упругие коэффициенты:
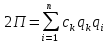
Уравнения малых колебаний системы около положения устойчивого равновесия.
Подставляя в уравнение Лагранжа выражения для кинетической и потенциальной энергий b принимая, что:
, можно получить систему дифференциальных уравнений, описывающих колебания системы:
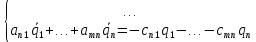
Общее решение данной системы уравнений определяет колебания механической системы.
С помощью линейных преобразований следующего вида:
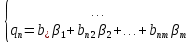
уравнения КЭ и ПЭ преобразуются:
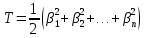
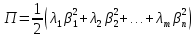
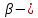нормальные координаты системы. В таких координатах уравнение малых колебаний имеет форму:
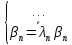
Решение имеет вид:
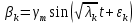
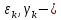из начальных условий.
Ввиду того, что изменение нормальных координат происходит независимо друг от друга, подбирая НУ можно сделать все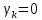
, кроме одного.
Во время движения системы:
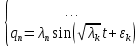
Обобщенные координаты будут изменятся по одному гармоническому закону с одной частотой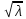
. Система при этом совершает главные (собственные) колебания. Система с степеней свободы может совершать колебаний со своими главными частотами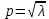 
.
В реальных условиях система совершает сложные колебания, которые представляют собой наложение собственных гармонических колебаний.
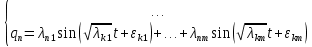
На практике интегрирование системы дифференциальных уравнений малых колебаний сводится к нахождению частных решений, соответствующих главным колебаниям, т.к. именно на этих частотах возможно разрушение материала. Если система совершает одно из главных колебаний
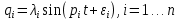
Подставляя данное выражение в систему уравнений малых колебаний, получим систему алгебраических уравнений с неизвестными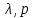
.
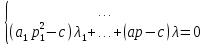
Если определитель матрицы коэффициентов при λ равен нулю, то можно определить частоты колебаний системы через уравнение частот:
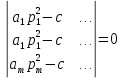
Собственные формы колебаний.
Частотное уравнение определяет собственных частот 
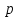. Они различны и возрастают. Свойства: не зависят от НУ; число перемен знака при деформации тела при колебании собственной формой частотой 
-го порядка равно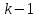 
.
Детали или механизмы системы на практике являются сложной упругой системой с бесконечным числом степеней свободы. Для определения положения точек при колебаниях в любой момент времени необходимо найти функцию времени и координат точек. При расчетах упругая система заменяется более простой системой с конечным числом степеней свободы – приведенная система.
Кинематическая энергия системы с
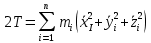
степеней свободы: Если выполняется переход к обобщенным координатам:
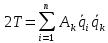
инерционные коэффициенты.Для колебаний возле положения устойчивого равновесия разложение коэффициентов
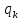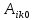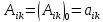
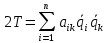
в ряд по степеням ограничивается рассмотрением постоянного коэффициента , остальные же не рассматриваются ввиду их малости. Потенциальная энергия системы может быть выражена через упругие коэффициенты:
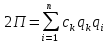
Уравнения малых колебаний системы около положения устойчивого равновесия.
Подставляя в уравнение Лагранжа выражения для кинетической и потенциальной энергий b принимая, что:
, можно получить систему дифференциальных уравнений, описывающих колебания системы: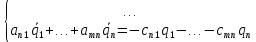 Общее решение данной системы уравнений определяет колебания механической системы.
-
Нормальные координаты и главные колебания.
С помощью линейных преобразований следующего вида:
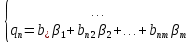
уравнения КЭ и ПЭ преобразуются:
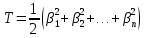
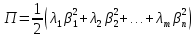
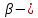нормальные координаты системы. В таких координатах уравнение малых колебаний имеет форму: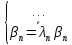 Решение имеет вид:
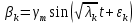
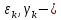из начальных условий.Ввиду того, что изменение нормальных координат происходит независимо друг от друга, подбирая НУ можно сделать все
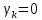, кроме одного.Во время движения системы:
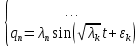
Обобщенные координаты будут изменятся по одному гармоническому закону с одной частотой
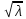. Система при этом совершает главные (собственные) колебания. Система с степеней свободы может совершать колебаний со своими главными частотами 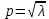.В реальных условиях система совершает сложные колебания, которые представляют собой наложение
собственных гармонических колебаний. -
Уравнение частот, собственные формы колебаний и их свойства
На практике интегрирование системы дифференциальных уравнений малых колебаний сводится к нахождению частных решений, соответствующих главным колебаниям, т.к. именно на этих частотах возможно разрушение материала. Если система совершает одно из главных колебаний
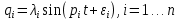
Подставляя данное выражение в систему уравнений малых колебаний, получим систему алгебраических уравнений с неизвестными
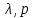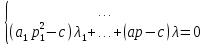
. Если определитель матрицы коэффициентов при λ равен нулю, то можно определить частоты колебаний системы через уравнение частот:
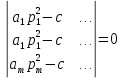
Собственные формы колебаний.
Частотное уравнение определяет
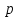собственных частот . Они различны и возрастают. Свойства: не зависят от НУ; число перемен знака при деформации тела при колебании собственной формой частотой -го порядка равно 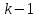.