ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
изменения частоты вращения не учитываются, т.к. не сказываются на ресурсе. Имитируются участки меняющихся напряжений.
Подбирается испытательный цикл по частоте вращения, температуре и другим параметрам так, чтобы повреждаемость детали от малоцикловой усталости была аналогична полетному циклу. Степень подобия условий нагружения на установке оценивается по величине повреждаемости. Коэффициент соответствия: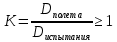
. Повреждаемость определяется расчетами напряжений. На основании 
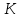определяется длительность испытаний с учетом требуемого коэффициента запаса для подтверждения и назначения ресурса.
ЭЦИ валов. Валы нагружают моментом и изгибающей силой.
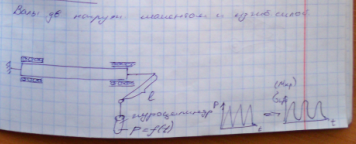
ЭЦИ корпусов и элементов подвески двигателя.
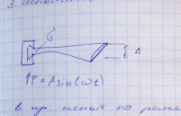
Усталостные испытания лопаток.
1) Закрепление лопатки соответствует закреплению при работе.
2) Тарировка – установление связи между величиной деформации и возникающими напряжениями (перемещениями).
3) Испытания профиля.
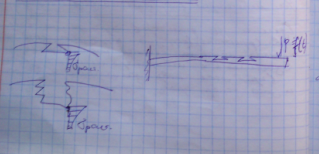
Способы динамического возбуждения: вибростенд, пульсирующий поток.
4) Испытания замка лопатки. Фактор – феттинг-коррозия из-за микроперемещений контактных плоскостей диска и замка. Повреждается защитный слой на поверхности и ускоряется коррозия.
P1 – высокочастотная нагрузка, P2 – низкочастотная (малоцикловая усталость).
Испытания ободных частей дисков.
Способы измерения деформации и перемещений.
1) С помощью тензорезисторов, сопротивление которых изменяется в зависимости от длины. Перед измерением проводят тарировку датчиков. Один из партии тензорезисторов устанавливается на балку известного сечения и длины. В точке установки датчика теоретически известны напряжения и деформации. Затем строится функция тензодатчика.
2) Оптические измерения с перемещением точек на поверхности детали: а) с помощью меток или сеток на поверхности и оптических микроскопов; б) лазерная интерферометрия.
Третья стратегия управления ресурсом.
Установление и назначение ресурса деталям двигателя выполняется расчетным путем. Обязательным условием применения данной методики является экспериментальное исследование прочности материала на образцах, что позволяет учитывать статистическое рассеяние данных параметров.
Физическая система называется колебательной, если все или некоторые ее величины, определяющие ее состояние, изменяются периодически.
Связи механической системы – ограничения, стесняющие движение системы и осуществляемые какими-либо другими материальными телами. Могут быть представлены в виде уравнений, которым должны удовлетворять координаты точек системы и производные от координат по времени.
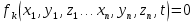
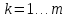
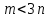
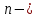количество точек, 
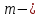количество связей.
Обобщенные (независимые) координаты. Пусть система из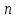
точек, 
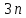координат которых определяет ее положение в пространстве в момент времени 
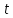, подчинена 
связям. В этом случае координат могут быть выражены через остальные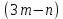 
независимые координаты, которым можно давать любые изменения без нарушения связей. Число независимых от связей координат системы есть число степеней свободы. Вместо декартовых координат в качестве независимых обычно выбирают другие, связанные с ними величины. Они называются обобщенными координатами и обозначаются
, 
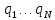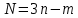. Число обобщенных координат долдно быть равно числу независимых величин; однозначно определять положение системы и через них должны быть выражены все декартовые координаты системы в виде уравнений:
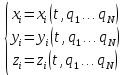
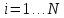
Виртуальные перемещения – воображаемые бесконечно-малые перемещения системы из одного положения в данный момент времени в другое положение, допускаемое связями в тот же момент времени, без освобождения от связей. Такие изменения координат при фиксированном времени обозначаются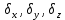
. В отличие от 
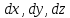за время 
.
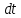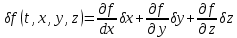
Обобщенные силы – преобразованные к обобщенным координатам выражения виртуальной работы сил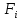
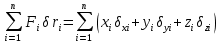
Выражение виртуальных перемещений через обобщенные координаты:
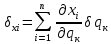
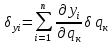
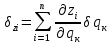
Выражение для обобщенной силы:
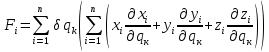
Обобщенная сила:
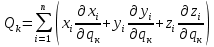
Может быть определена через потенциальную энергию:
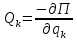
Условие равновесного состояния системы.
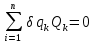
Условие для консервативных систем, где первое условие выполняется автоматически.
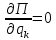
Консервативная система – система, в которой работа сил по перемещению точки по замкнутому контуру равна нулю, т.е. отсутствуют силы трения и рассеивание энергии.
Для исследования колебательных систем с конечным числом степеней свободы используются уравнения Лагранжа в обобщенных координатах, составленные в предположении о том, что связи, наложенные на систему, идеальны; уравнения не содержат реакций связей; входящие в уравнения величины, определяющие движения системы, непосредственно связаны обобщенными силами.
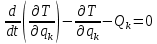
Для консервативных систем уравнение Лагранжа записывается через потенциальную энергию:
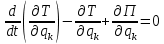
В этом случае энергия характеризует полную механическую энергию системы.
Колебания системы с одной степенью свободы.
Система с одной СС – система, положение которой в пространстве однозначно определяется заданием одной обобщенной координаты. Например математический маятник движется по закону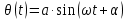
, где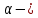 
начальная фаза, 
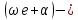фаза колебаний, 
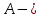амплитуда.
Уравнения малых свободных колебаний системы с одной СС.
Колебания называются свободными, если скорость изменения состояния системы определяется только состоянием самой системы. Такая система – линейный осциллятор.
Система консервативна, уравнение Лагранжа:
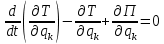
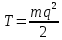
Сопротивление среды равно нулю, поэтому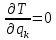
Потенциальная энергия оценивается через жесткость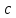
системы: 
/
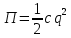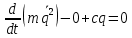
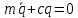
Общее решение: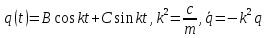
.
Подстановка для решения: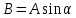
, 
, 
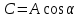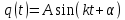
Начальные условия для решения:
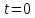
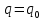
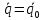
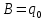
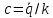
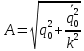
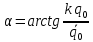
Свободные колебания при наличии сопротивления.
В этом случае на систему действует сила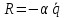
:
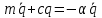
Введем отношение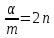
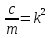, тогда
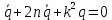
Подбирается испытательный цикл по частоте вращения, температуре и другим параметрам так, чтобы повреждаемость детали от малоцикловой усталости была аналогична полетному циклу. Степень подобия условий нагружения на установке оценивается по величине повреждаемости. Коэффициент соответствия:
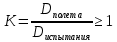. Повреждаемость определяется расчетами напряжений. На основании 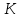определяется длительность испытаний с учетом требуемого коэффициента запаса для подтверждения и назначения ресурса.ЭЦИ валов. Валы нагружают моментом и изгибающей силой.
ЭЦИ корпусов и элементов подвески двигателя.
Усталостные испытания лопаток.
1) Закрепление лопатки соответствует закреплению при работе.
2) Тарировка – установление связи между величиной деформации и возникающими напряжениями (перемещениями).
3) Испытания профиля.
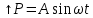
Способы динамического возбуждения: вибростенд, пульсирующий поток.
4) Испытания замка лопатки. Фактор – феттинг-коррозия из-за микроперемещений контактных плоскостей диска и замка. Повреждается защитный слой на поверхности и ускоряется коррозия.
P1 – высокочастотная нагрузка, P2 – низкочастотная (малоцикловая усталость).
Испытания ободных частей дисков.
Способы измерения деформации и перемещений.
1) С помощью тензорезисторов, сопротивление которых изменяется в зависимости от длины. Перед измерением проводят тарировку датчиков. Один из партии тензорезисторов устанавливается на балку известного сечения и длины. В точке установки датчика теоретически известны напряжения и деформации. Затем строится функция тензодатчика.
2) Оптические измерения с перемещением точек на поверхности детали: а) с помощью меток или сеток на поверхности и оптических микроскопов; б) лазерная интерферометрия.
Третья стратегия управления ресурсом.
Установление и назначение ресурса деталям двигателя выполняется расчетным путем. Обязательным условием применения данной методики является экспериментальное исследование прочности материала на образцах, что позволяет учитывать статистическое рассеяние данных параметров.
-
Теория колебаний. Связи. Обобщенные координаты. Виртуальные перемещения. Обобщенные силы. Условия равновесия.
Физическая система называется колебательной, если все или некоторые ее величины, определяющие ее состояние, изменяются периодически.
Связи механической системы – ограничения, стесняющие движение системы и осуществляемые какими-либо другими материальными телами. Могут быть представлены в виде уравнений, которым должны удовлетворять координаты точек системы и производные от координат по времени.
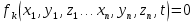
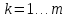
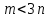
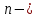количество точек, 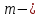количество связей.Обобщенные (независимые) координаты. Пусть система из
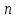точек, 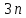координат которых определяет ее положение в пространстве в момент времени 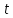, подчинена связям. В этом случае координат могут быть выражены через остальные 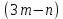независимые координаты, которым можно давать любые изменения без нарушения связей. Число независимых от связей координат системы есть число степеней свободы. Вместо декартовых координат в качестве независимых обычно выбирают другие, связанные с ними величины. Они называются обобщенными координатами и обозначаются
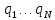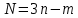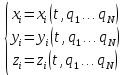
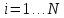
, . Число обобщенных координат долдно быть равно числу независимых величин; однозначно определять положение системы и через них должны быть выражены все декартовые координаты системы в виде уравнений: Виртуальные перемещения – воображаемые бесконечно-малые перемещения системы из одного положения в данный момент времени в другое положение, допускаемое связями в тот же момент времени, без освобождения от связей. Такие изменения координат при фиксированном времени обозначаются
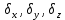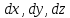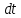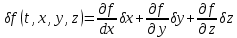
. В отличие от за время . Обобщенные силы – преобразованные к обобщенным координатам выражения виртуальной работы сил
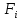
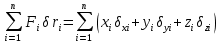
Выражение виртуальных перемещений через обобщенные координаты:
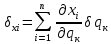
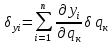
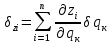
Выражение для обобщенной силы:
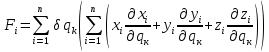
Обобщенная сила:
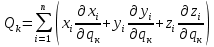
Может быть определена через потенциальную энергию:
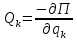
Условие равновесного состояния системы.
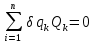
Условие для консервативных систем, где первое условие выполняется автоматически.
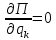
Консервативная система – система, в которой работа сил по перемещению точки по замкнутому контуру равна нулю, т.е. отсутствуют силы трения и рассеивание энергии.
-
Уравнение Лагранжа. Свободные колебания системы с одной степенью свободы (начальные условия, уравнения, определения). Свободные колебания системы при сопротивлении.
Для исследования колебательных систем с конечным числом степеней свободы используются уравнения Лагранжа в обобщенных координатах, составленные в предположении о том, что связи, наложенные на систему, идеальны; уравнения не содержат реакций связей; входящие в уравнения величины, определяющие движения системы, непосредственно связаны обобщенными силами.
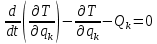
Для консервативных систем уравнение Лагранжа записывается через потенциальную энергию:
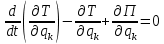
В этом случае энергия характеризует полную механическую энергию системы.
Колебания системы с одной степенью свободы.
Система с одной СС – система, положение которой в пространстве однозначно определяется заданием одной обобщенной координаты. Например математический маятник движется по закону
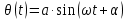, где 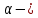начальная фаза, 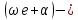фаза колебаний, 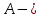амплитуда.Уравнения малых свободных колебаний системы с одной СС.
Колебания называются свободными, если скорость изменения состояния системы определяется только состоянием самой системы. Такая система – линейный осциллятор.
Система консервативна, уравнение Лагранжа:
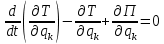
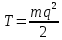
Сопротивление среды равно нулю, поэтому
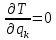
Потенциальная энергия оценивается через жесткость
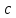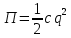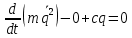
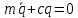
системы: / Общее решение:
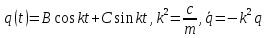.Подстановка для решения:
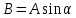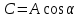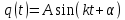
, , Начальные условия для решения:
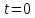
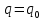
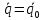
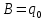
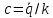
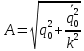
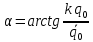
Свободные колебания при наличии сопротивления.
В этом случае на систему действует сила
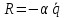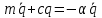
: Введем отношение
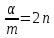
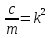, тогда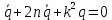 - 1 2 3 4 5