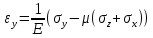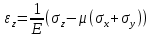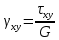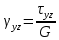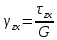ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 65
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
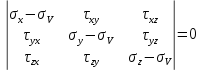
Разворачиваем определитель, учитывая парность касательных напряжений:
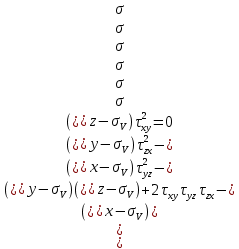
Путем сокращения получаем:
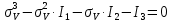
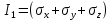
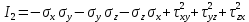
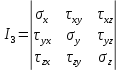
Корни полученного характеристического кубического уравнения напряженного состояния представляют собой величины главных напряжений
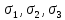 . Для определения ориентации площадки, где действует
. Для определения ориентации площадки, где действует 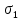 в уравнение системы
в уравнение системы 


вносится значение
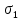 вместо
вместо 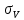 , далее определяются значения l,m,n с учетом теоремы косинусов, определяются l1,m1,n1. Аналогично для 2 и 3.
, далее определяются значения l,m,n с учетом теоремы косинусов, определяются l1,m1,n1. Аналогично для 2 и 3.Инварианты напряженного состояния в точке.
Расположение главных площадок и значение главных напряжений в точке тела зависит от действующих напряжений и не зависит от системы координат и ее изменения. Таким образом, коэффициенты характеристического уравнения напряженного состояния инвариантны к изменению системы координат. Инвариант - коэффициент характеристического уравнения напряженного состояния, не зависящий от системы координат.

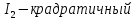
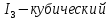
Тензор напряжений.
Напряженное состояние в точке тела описывают с помощью скалярных величин напряжений или 3 векторов, включающих 3 скалярные величины.
Величины, описываемые векторами, принято называть тензорами.
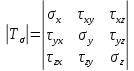
Тензор симметричен в силу парности касательных напряжений, что позволяет характеризовать его 6 скалярными величинами.
-
Дифференциальные уравнения равновесия.
Рассмотрим равновесие элемента тела, примыкающего к точке А с координатами (x,y,z).
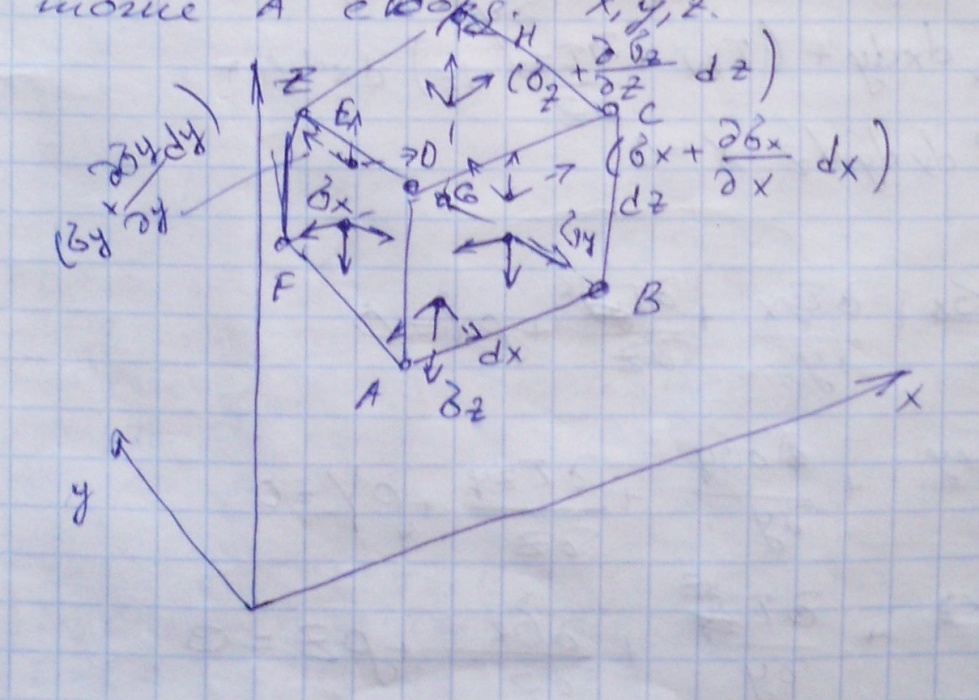
На гранях, содержащих точку А напряжения имеют следующие значения:
АDEF:
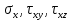
ABCD:
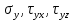
ABGF:
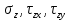
AGBC: (
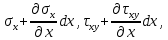
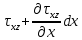 )
)HGFE: (
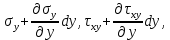
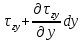 )
)HCDE: (
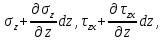
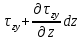 )
)Кроме напряжений на гранях, на объем действуют массовые силы X,Y,Z. Спроецировав действующие силы на оси координат, получим дифференциальное уравнение равновесия:
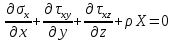
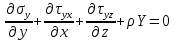
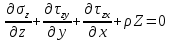
Уравнения равновесия для моментов:
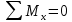
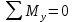
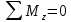
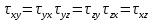
-
Краевые условия для напряжений.
Равновесие элементов, примыкающих к поверхности тела, обеспечивается силами, действующими на поверхности. И наоборот, силы на поверхности уравновешиваются напряжениями, возникающими в теле.
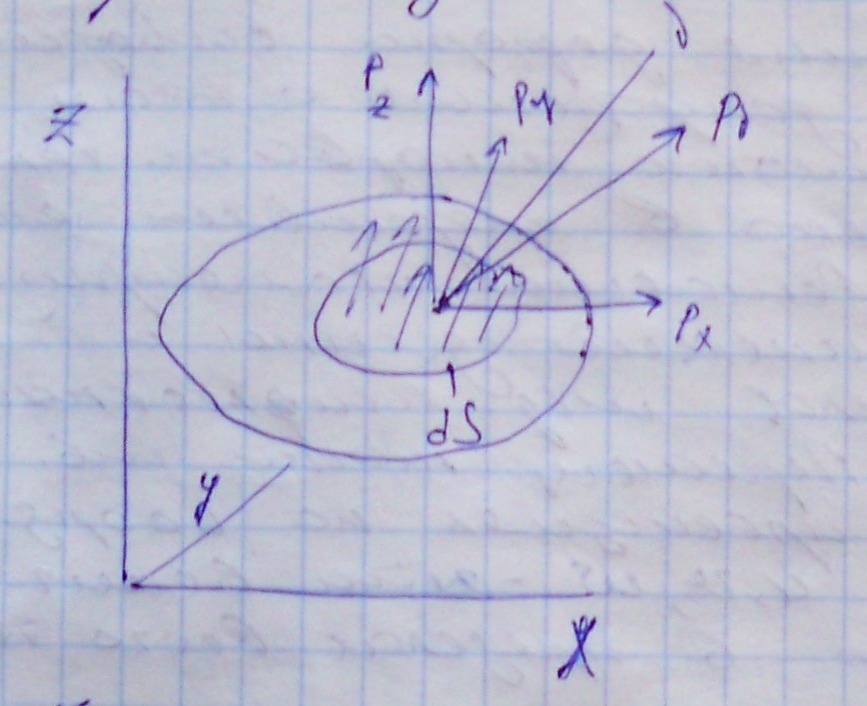
Нагрузку на поверхности тела можно представить как вектор напряжений
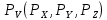 , действующий на поверхности dS. Элемент поверхности dS, ввиду его малости, можно рассматривать как площадку с нормалью V, напряжение, возникшее в теле можно связать с нагрузками на поверхности, используя уравнение системы
, действующий на поверхности dS. Элемент поверхности dS, ввиду его малости, можно рассматривать как площадку с нормалью V, напряжение, возникшее в теле можно связать с нагрузками на поверхности, используя уравнение системы 

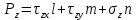
Получим краевые условия:
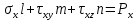
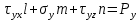
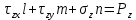
-
Д еформированное состояние в точке, тензор деформаций. Инварианты тензора деформаций. Связь деформаций с перемещениями точек твердого тела (уравнения Коши).
еформированное состояние в точке, тензор деформаций. Инварианты тензора деформаций. Связь деформаций с перемещениями точек твердого тела (уравнения Коши).
Определение понятия деформации выводится на основании допущения о том, что перемещение точек неподвижного тела возможно только вследствие его деформации. Решается геометрическая задача об изменении длины и взаимных углов между элементами тела. Перемещение точки твердого тела после деформации в проекциях на координатные оси обозначают
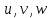 - эти величины малы и непрерывны в пределах всего тела. Рассмотрим элементарный объем:
- эти величины малы и непрерывны в пределах всего тела. Рассмотрим элементарный объем:Если тело подвергается деформации и
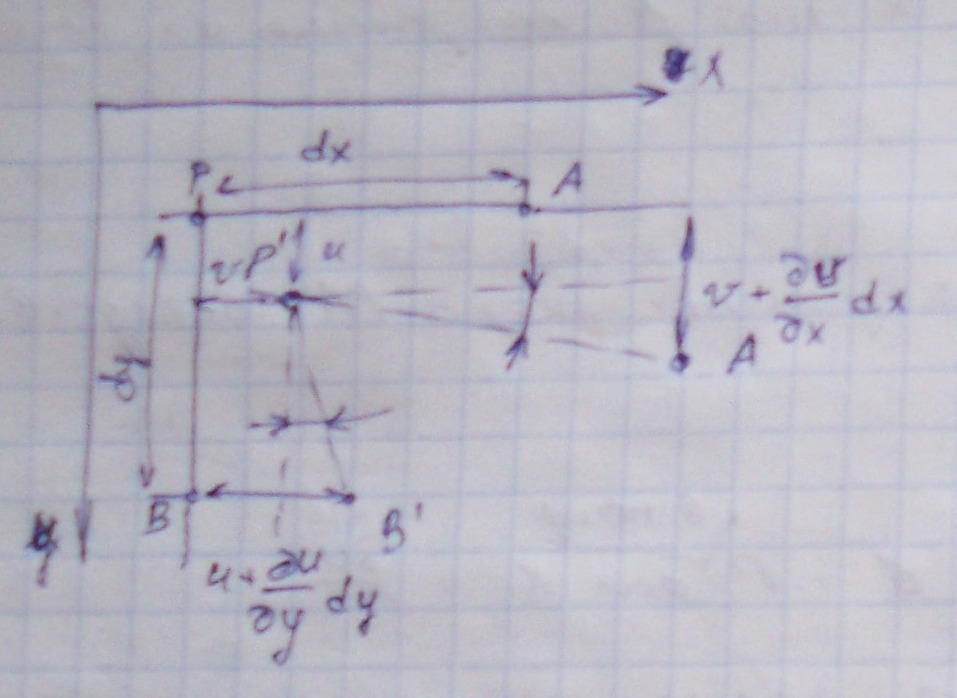
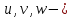 компоненты перемещения в точке Р, то перемещение в напряжении оси Х точки А на длине dx составит следующее:
компоненты перемещения в точке Р, то перемещение в напряжении оси Х точки А на длине dx составит следующее: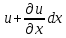
Соответственно увеличение длины ребра РА вследствие деформации равно
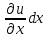 . Относительное удлинение в точке Р в направлении оси Х соответственно
. Относительное удлинение в точке Р в направлении оси Х соответственно 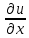 . Аналогичное рассуждение справедливо для других осей
. Аналогичное рассуждение справедливо для других осей 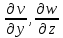 .
. Относительное удлинение обозначают
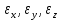 - и называют линейной деформацией 1 рода:
- и называют линейной деформацией 1 рода: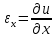
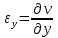
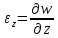
Кроме линейных деформаций твердое тело можно деформировать без изменения объема, сдвигом:
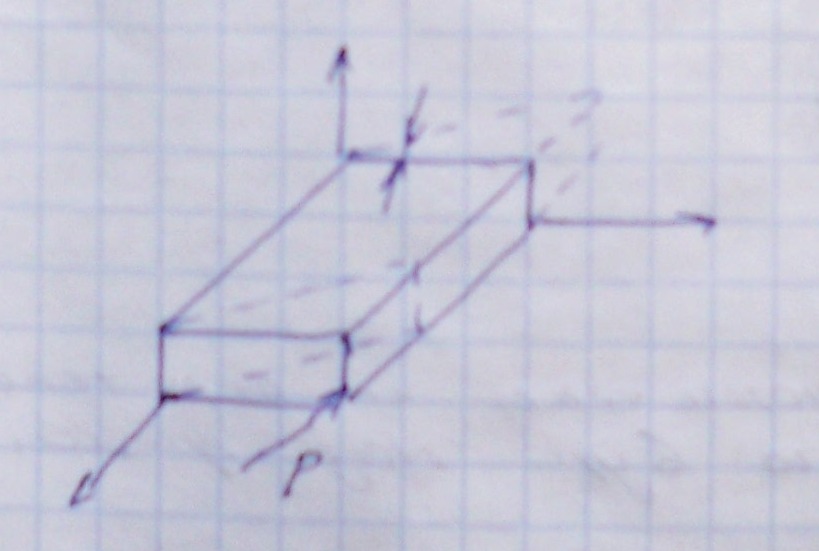
Рассмотрим изменение угла между элементами РА и РВ в плоскости XY
После перемещения, линейный элемент РА переместиться в новое положение P’A’и образует с начальным положением угол
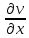 . Аналогично P’В’ образует угол
. Аналогично P’В’ образует угол 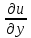 . Первоначальный угол между элементами РВ и РА равный 90
. Первоначальный угол между элементами РВ и РА равный 90 уменьшиться на величину
уменьшиться на величину 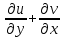 - эта величина представляет собой деформацию сдвига между плоскостями и обозначается
- эта величина представляет собой деформацию сдвига между плоскостями и обозначается 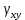
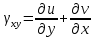

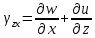
Связь перемещения точек тела и деформаций тела выражается с помощью 6 уравнений, называемых формулами Коши:

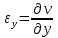
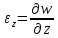
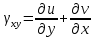

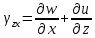
6 величин, описывающих деформацию тела, образуют тензор деформаций:
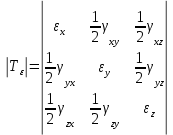
Тензор симметричен относительно главной диагонали, вследствие парности угловых деформаций
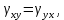
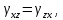
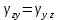
Деформации инвариантны к преобразованию системы координат:
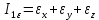
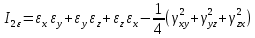
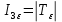
Компоненты тензора деформации не могут быть произвольными величинами, не связанными с
 - величинами перемещений. Для определения перемещений
- величинами перемещений. Для определения перемещений  по величинам деформации они должны удовлетворять 6 уравнениям неразрывности (сплошности):
по величинам деформации они должны удовлетворять 6 уравнениям неразрывности (сплошности):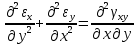
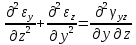
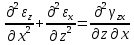
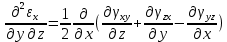
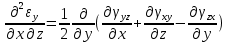
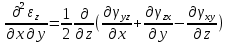
Если уравнения неразрывности деформации не удовлетворяются, то деформация тела происходит с разделением на фрагменты или с образованием надрывов на поверхности.
-
Закон Гука для упругой изотропной среды.
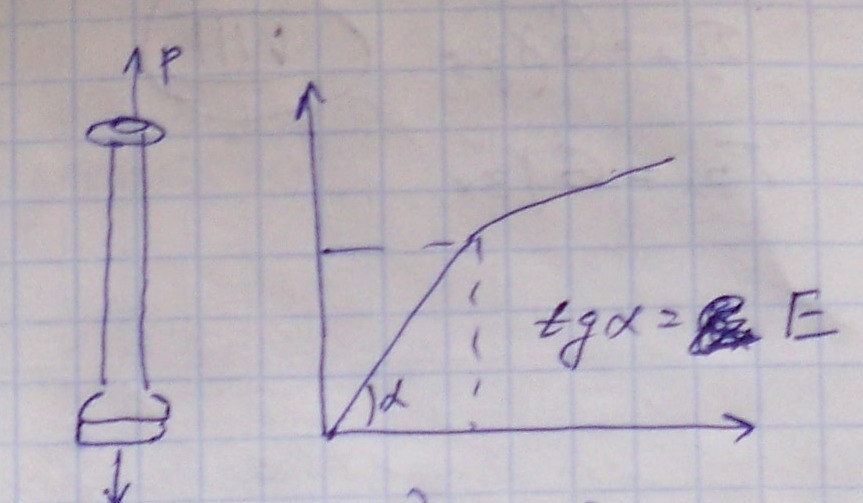
Опытным путем установлено, что процесс деформации конструкционных материалов разделяется на несколько этапов:
-
Характеризуется линейной зависимостью между напряжениями и деформациями.
Р. Гук в 1679 году первым опубликовал о линейной связи деформаций и напряжений. Линейное соотношение между тензором напряжений и тензором деформаций принято называть законом Гука.
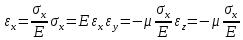
Для трехмерного напряженного состояния закон Гука приобретает другую форму: