1. 
   Модели прочностной надежности.
   

Модель - совокупность представлений, зависимостей, условий, ограничений, описывающих процесс или явление, способ отображения или описания реальности.Надежность - свойство изделия выполнять заданные функции, сохраняя эксплуатационные показатели в течение требуемого промежутка времени или времени эксплуатации.Прочностная надежность - отсутствие отказов, связанных с разрушением или недопустимыми деформациями конструкции.Основная характеристика надежности - вероятность безотказной работы. 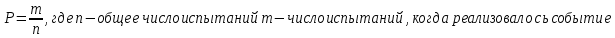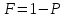Вероятность Вероятность отказа, разрушения - Основным методом оценки прочностной надежности является определение запасов прочности - 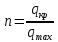, где 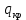- критическая величина параметра, приводящего к отказу или разрушению; 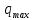- наибольшее значение параметра, достигаемое при эксплуатации. Условие прочностной надежности: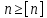 Правильный выбор каждой модели определяет достоверность результатов.

1. 
   Модели материалов
   

В зависимости от масштаба рассмотрения материалов выделяют:

• 
  Физические модели материалов - уровень атомов и кристаллической решетки
  
• 
  Инженерно-физические модели материалов - уровень зерна сплавов, волокон композитов, уровень углеродных компонентов, из которых состоит материал
  
• 
  Инженерные модели материалов - уровень тел деталей, материал рассматривается как сплошное и однородное тело, при этом определяются свойства неоднородных элементов структуры предыдущей модели
  

В моделях прочностной надежности используют инженерные модели, материал рассматривается как сплошное однородное тело, что позволяет использовать методы математического анализа. В зависимости от свойств материала модель наделяют свойствами упругости, пластичности, ползучести и др.

---

Упругость - способность тела восстанавливать форму после снятия нагрузки.Пластичность - свойство тела сохранять полностью или частично форму приобретенную под действием нагрузки (после нагрузки).Ползучесть - свойство тела увеличивать деформацию (размеры) под действием нагрузки.

2. 
   Модели формы
   

Описание конструкции тела с помощью стандартных элементов:

• 
  Стержни
  
• 
  Пластины
  
• 
  Оболочки
  
• 
  Пространственные тела
  

Описание формы реального тела стандартными элементами позволяет описать тело математическими выражениями или их совокупностью.

3. 
   Модели нагружения
   

• 
  Сосредоточенные силы
  
• 
  Распределенные силы
  
• 
  Объемные или массовые силы - действуют на все единицы массы
  

Посредством их описывают действия внешних сил. В зависимости от времени действия нагрузки разделяют на:

• 
  Стационарные (постоянны по времени)
  
• 
  Нестационарные (изменяются с течением времени)
  

Модели нагружения содержат схематизацию нагрузок: по величине распределения, времени действия, действию внешних полей и сред.Действие внешней среды - действие окружающей среды, приводящие к изменению условий нагружения (процессы окисления, коррозии)

4. 
   Модели разрушения
   

Это уравнения и условия, связывающие параметры работоспособности в момент разрушения с параметрами прочности. Основные модели разрушения:

• 
  Статическое разрушение - происходит при достижении пределов прочности материалов при однократном или многократном (не более 100) приложении нагрузки
  
• 
  Длительное статическое разрушение - исчерпание прочности материала при постоянной нагрузке вследствие протекания процессов ползучести
  
• 
  Малоцикловое разрушение - исчерпание прочности материала под действием переменных нагрузок высокого уровня (100 - 10000 циклов нагружения)
  
• 
  Многоцикловое разрушение - исчерпание прочности материала при действии переменных нагрузок низкого уровня (более 10000 циклов нагружения)
  

Конечной целью проектирования является работоспособная надежная конструкция.

2. 
   Нормальные и касательные напряжения, правила знаков.
   

Под действием на тело внешних сил в теле возникают внутренние силы - реакции. Мысленно рассекая тело под действием внешних сил, отброшенную часть необходимо заменить силами взаимодействия.

---

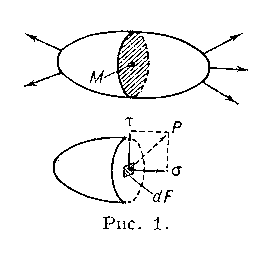
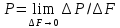
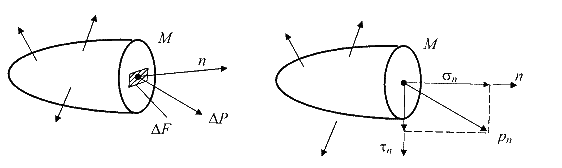
Характеристика интенсивности внутренних сил взаимодействия являются напряжения:В точке тела они равны предельному отношению. Напряжения в точке тела зависят от ориентации плоскости сечения проходящего через рассматриваемую точку.Р - есть вектор, раскладываемый на нормальные и касательные компоненты в рассматриваемой точке.Напряжения состояния в точке тела.Для оценки прочности любого тела необходимо знать напряжения в наиболее опасных точках. Элементарный параллелепипед - параллелепипед, вырезанный в теле тремя взаимно ортогональными плоскостями бесконечно малого размера.В рассматриваемой точке тела выделим элементарный параллелепипед размерами dx, dy, dz и разместим в данной точке прямоугольную систему координат. Те части тела, откинутые заменим напряжениями, действующими на гранях элементарного параллелепипеда. В общем случае действуют как касательные так и нормальные 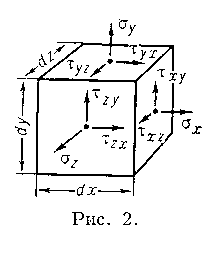напряжения. Вектора напряжений обозначаются 2 индексами: 1 - ось координат нормальная к площадке, на которой действует вектор; 2 - ось координат, к которой вектор параллелен. Если индекс одинаковый, пишется один из них.Правило знаков:Для нормальных напряжений:

• 
  За положительное направление нормального напряжения принимается направление, при котором тело растягивается
  
• 
  За отрицательное направление нормального напряжения принимается направление, при котором тело сжимается
  

Для касательных напряжений:

• 
  Если на площадке действует растягивающее нормальное напряжение, совпадающее по направлению с положительным направлением оси координат, то за положительное направление касательных напряжений принимается положительное направление осей координат, которым они параллельны
  
• 
  Если на площадке действует растягивающее нормальное напряжение, совпадающее по направлению с отрицательным направлением оси координат, то за положительное направление касательных напряжений принимается отрицательное направление осей координат, которым они параллельны.
  

---

3. 
   Свойство парности касательных напряжений. Виды напряженного состояния.
   

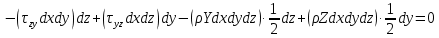
Из теоретической механики известно, что достаточным условием равновесия является равенство нулю суммы всех моментов и сил относительно любой из осей. Рассмотрим элементарный параллелепипед, находящийся в равновесии. Напряжения на его гранях приведем к силам, умножив на площадь граней. Момент векторов сил определим через длину граней.Сумма моментов относительно оси ОХ:Y,Z - составляющие массовой силы. 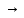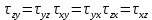Величины в последних скобках на 2 порядка меньше, поэтому они не учитываются, отсюдаКасательные напряжения, действующие в точке на ортогональных площадках равны.Виды напряженного состояния:

• 
  Одномерное напряженное состояние (один из 3 компонентов нормальных напряжений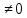 не равен нулю, все остальные = 0)
  
• 
  Плоское напряженное состояние ( )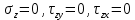
  
• 
  Объемное напряженное состояние (все компоненты )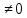
  

4. 
   Напряжения на произвольной косой площадке.
   

Зная напряжения на 3 ортогональных площадках, проходящих через одну точку, можно определить напряжения, действующие на любой другой плоскости, проходящей через эту точку.Произвольная площадка характеризуется вектором нормали V,который раскладывается на компоненты по осям x,y,z. 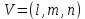. Эти компоненты являются косинусами углов между нормалью и осями координат. 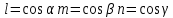- направляющие косинусы. 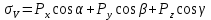- нормальное напряжение, действующее на произвольной площадке, равно сумме составляющих действующей силы по трем осям. (1)

---

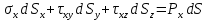
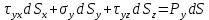
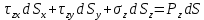
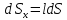
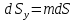
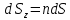
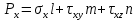
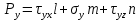
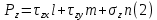
Выразим через напряжения на трех ортогональных плоскостях через условия равновесия:Подставим вместо Сократим на dS и получим:Подставим уравнение (2) в уравнение (1) получим:

5. 
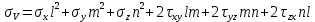
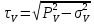
   Главные площадки и главные напряжения. Инварианты напряженного состояния в точке. Тензор напряжений.
   

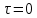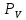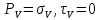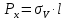
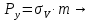
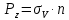
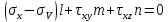
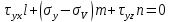
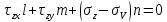
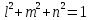
Главные площадки - площадки, на которых отсутствуют касательные напряжения. ( )Главные напряжения - напряжения, действующие на главных площадках.Пусть площадка главная, полное напряжение совпадает с нормальными ( )Для главной площадки получим соотношение:Неизвестными являются углы l,m,n. Дополнительным условием для нахождения этих соотношений является теорема косинусов. Из линейной алгебры следует, что система имеет решение если детерминант = 0.

---

Смотрите также файлы

• Введение (Задачи организации работы складского хозяйства строительной организации).docx

• Инструкция по просмотру результатов и подаче апелляций.docx

• Вопрос 1 Регулярно ли Вы питаетесь в ресторане быстрого обслуживания да, нет.docx

• Курсовой проект пм 01 Участие в проектировании зданий и сооружений мдк 01. 02 Проект производства работ Тема Проектирование проекта производства работ на возведение жилого дома с декоративной штукатуркой Курсовой проект выполнен.docx

• 1. Д. Исабековті пке драмасында суреттелген отбасылы мселе.docx